Определение 1. Отображение 
: 
называется инъективным или инъекцией, если два различных элемента из множества 
имеют образами при отображении два различных элемента из множества 
, т.е.
, 
.
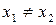
Например, отображение : приведенное на следующей схеме
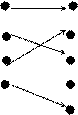
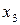
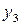
является инъекцией множества в множество . Здесь 
.
Определение 2. Отображение : называется сюръективным или сюръекцией, если каждый элемент из множества является образом при отображении по крайней мере одного элемента из , т.е.
такой, что 
, т.е. 
.
Сюръективное отображение – это отображение множества на множество .
Например, отображение :
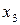
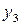
является сюръективным, а отображение 
:
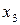
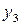
не является сюръективным.
Если 
при отображении : , то отображение - сюръективное.
Теорема. Отображение : биективно тогда и только тогда, когда оно инъективно и сюръективно одновременно.
Доказательство. Пусть : - биективно. Тогда каждый элемент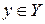 
является образом при отображении некоторого элемента 
, следовательно, отображение - сюръективно. А так как этот элемент 
- единственный, то из этого следует, что разным элементам соответствуют разные образы, т.е. отображение инъективно.
Обратно, пусть : - инъективно и сюръективно одновременно. Тогда в силу сюръекции , а ввиду инъективности отображения 
содержит единственный элемент.
Примеры.
1. 
, 
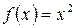
Отображение не сюръективно, т.к. элемент 
не является образом ни одного элемента из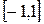 
. Оно не является и инъективным, т.к. два различных элемента 
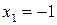и 
имеют образом один и тот же элемент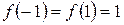 
.
2. : 
, 
Отображение сюръективно, но не инъективно.
3. 
: 
, 
Отображение сюръективно и инъективно одновременно, т.к. оно биективно.
