Определение. Пусть заданы два отображения
: 
, 
: 
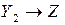
причем 
. Тогда определена композиция: 
: 
отображений 
и 
равенством 
.
Композиция является отображением, так как однозначно определен элемент 
, 
, и, следовательно, однозначно определен элемент 
.
Примеры.
1. : 
, 
.
, 
.
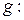
Проверим, определены ли композиции и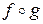 
.
В виду того, что 
, то композиция определена
, 
.
В силу того, что 
не является подмножеством множества 
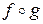, являющегося областью определения функции , то композиция не определена.
2. Пусть заданы два отображения 
и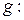 
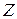
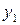
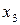
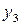
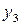
Здесь 
, поэтому композиция 
определена. Отображение переводит элемент 
в элемент 
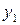, отображение переводит элемент 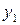в элемент , поэтому, аналогично 
, 
, 
.
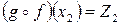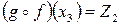Теорема. Операция композиции отображений ассоциативна, т.е. если 
, 
, 
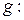
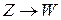, то
. (1)
Доказательство. Отметим, что отображения 
и 
определены (проверить самостоятельно). Далее, равенство (1) означает, что
.
Мы получили тождество, поэтому (1) доказано. Равенство (1) означает, что в выражении 
скобки можно расставлять произвольно.
