Зависимость потенциальной энергии электрона (Ф) в запорном слое от координаты и ширину этого слоя можно найти, решая уравнение Пуассона:
 (12)
(12)
где 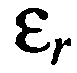 - относительная диэлектрическая проницаемость полупроводника; р(х) - плотность объемного или пространственного заряда в обедненном слое.
- относительная диэлектрическая проницаемость полупроводника; р(х) - плотность объемного или пространственного заряда в обедненном слое.
При наличии в полупроводнике только по одному типу донорной и акцепторной примеси и при их равномерном распределении по объему
 (13)
(13)
где  - концентрации ионизованных доноров и акцепторов, а n(х) и р(х) - концентрации электронов и дырок в области пространственного заряда (ОПЗ) контакта. Если примеси полностью ионизованы, то из уравнения электронейтральности следует
- концентрации ионизованных доноров и акцепторов, а n(х) и р(х) - концентрации электронов и дырок в области пространственного заряда (ОПЗ) контакта. Если примеси полностью ионизованы, то из уравнения электронейтральности следует

где Nd и Na — полные концентрации примесных атомов. В термодинамически равновесных условиях, когда через контакт металл — полупроводник не течет ток, для случая невырожденного полупроводника имеем
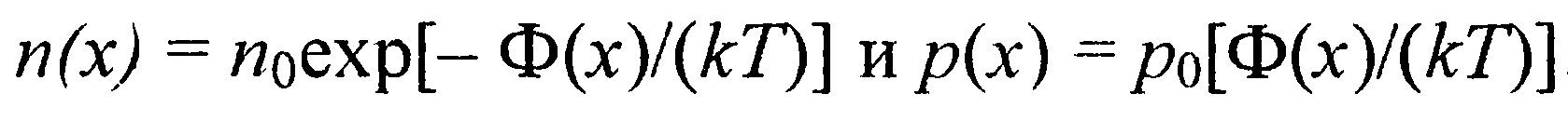
Тогда
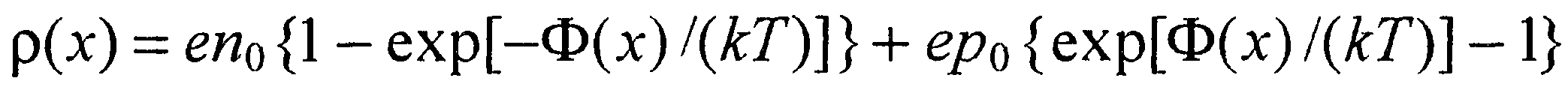 (14)
(14)
Плотность объемного заряда в запорном слое задается только зарядом полностью ионизованных доноров. Такой запорный слой называется слоем Шоттки.
Для слоя Шоттки в полупроводнике n-типа уравнение Пуассона запишется в виде
 (15)
(15)
Это уравнение решается при следующих граничных условиях:
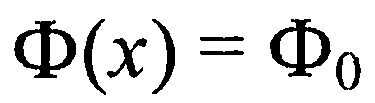 (16) при х=0
(16) при х=0
 (17) при x=d
(17) при x=d
Дважды интегрируя уравнение 15 с учетом граничных условий, получим
 (18)
(18)
Тогда напряженность контактного поля в ОПЗ будет иметь вид
 (19)
(19)
При х = 0 из уравнения 18 следует, что
 (20)
(20)
Отсюда можно определить ширину слоя Шотки, зная максимальный изгиб зон Фо:
 (21)
(21)
Предполагая, что изгиб зон в ОПЗ полностью обусловлен контактной разностью потенциалов, и пренебрегая падением напряжения в зазоре между металлом и полупроводником, с учетом выражения

можем записать
 (22)
(22)
Из формулы (22) видно, что слой Шоттки будет тем шире, чем больше разность термодинамических работ выхода маталла и полупроводника. С другой стороны, увеличение n0 приводит к уменьшению d.






