Денежные потоки, возникающие в разные моменты времени, имеют разную ценность и для сопоставления между собой приводятся к одному моменту времени. Неодинаковая ценность денежных потоков определяется в первую очередь действием объективных экономических законов, а не инфляцией, как кажется на первый взгляд. Для учета инфляции в экономических расчетах изменения ценности денежных потоков во времени, как правило, используются специальные методы, применяемые к ниже приведенным функциям финансовой математики.
Процессы преобразования текущей и будущей стоимости называются капитализацией и дисконтированием. Капитализация денежных потоков – это процедура приведения текущего значения денежных потоков к их будущей ценности. Дисконтирование денежных потоков – это процедура приведения будущих значений денежных потоков к их ценности на текущий (базовый) момент времени.
Дисконтирование (капитализация) денежных потоков осуществляется путем умножения их значения на коэффициент дисконтирования (капитализации) в текущий период.
Процессы капитализации и дисконтирования денежных потоков базируются на определении сложного процента. Сложный процент – это процедура начисления процентов как на основную сумму, так и на невыплаченные проценты, начисленные за предыдущий период. Базовой формулой начисления сложного процента является
 ,
,
где kn – коэффициент капитализации процентов после n периодов;
r – годовая ставка дохода (норма дисконта, ставка дисконтирования, норма капитализации, норма доходности);
n – количество периодов накоплений (например, число лет, в течение которых происходит накопление).
В практике оценки эффективности инвестиционных проектов обычно используется следующая формула определения коэффициента дисконтирования:
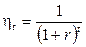 ,
,
где r – норма дисконта;
t – текущий период.
Например, она используется при определении таких показателей, как чистый дисконтированный доход, внутренняя норма доходности, индекс рентабельности инвестиций и т.п. Это связано прежде всего с тем, что все значения денежных потоков (от инвестиционной, операционной, финансовой деятельности) приводятся к базовому моменту оценки и на основе сопоставления суммарных приведенных эффектов и инвестиционных затрат принимаются решения о целесообразности реализации инвестиционного проекта.
Основными функциями финансовой математики, используемыми в экономике недвижимости, являются шесть функций сложного процента:
1. Будущая стоимость денежной единицы – FV (Future value);
2. Будущая стоимость аннуитета – FVA (Future value of an annuity);
3. Фактор фонда возмещения – SFF (Sinking fund factor);
4. Текущая стоимость денежной единицы – PV (Present value);
5. Текущая стоимость аннуитета – PVA (Present value of annuity);
6. Взнос на амортизацию денежной единицы – IAO (Installment of amortize one).
Будущая стоимость денежной единицы позволяет определить будущую стоимость инвестированной денежной единицы исходя из предполагаемых нормы доходности, срока накопления и периодичности начисления процента:
 ,
,
где FV – будущая стоимость денежного потока;
PV – текущая стоимость денежного потока;
n – число лет, в течение которых происходит накопление.
Приведенная формула справедлива, если начисление процентов происходит один раз в год. При более частом начислении процентов (например, раз в квартал, раз в месяц и т.п.) формула будет выглядеть следующим образом:
 ,
,
где m – частота начисления процентов в год.
Из приведенных формул видно, что чем чаще начисляются проценты, тем больше накопленная сумма. Таким образом, на практике выделяют номинальную и эффективную ставки дохода. Годовая эффективная ставка дохода отличается от годовой номинальной, так как учитывает капитализацию процентов (частоту начисления процентов в год).
На практике, как правило, используются денежные потоки не с единичными платежами, произведенными в определенный момент времени, а с серией платежей, происходящих в различные моменты времени. Если платежи происходят через строго определенные промежутки времени, то такая серия называется аннуитетом.
Аннуитеты разделяются на следующие виды: равномерные и неравномерные, обычные и авансовые. Равномерным аннуитетом называется аннуитет, состоящий из серии равновеликих платежей. Противоположностью ему является неравномерный аннуитет, при котором величина платежей может быть разной в различных платежных периодах. Аннуитет называется обычным (постнумерандо), если платежи осуществляются в конце каждого платежного периода, и авансовым (пренумерандо), если платежи производятся в начале платежного периода.
В случае использования обычных равномерных аннуитетов имеет место геометрическая прогрессия, поэтому, применив известную из курса математики формулу суммы членов геометрической прогрессии:
 ,
,
где b1 – первый член геометрической прогрессии;
q – знаменатель геометрической прогрессии,
можно получить выражение для будущей стоимости аннуитета:
 ,
,
где PMT – величина аннуитета (равномерного платежа).
В случае использования авансового аннуитета применяется следующую формула:
 .
.
При внесении аннуитетов чаще, чем один раз в год, соответственно чаще накапливается процент. Тогда ранее полученная формула примет вид:
 .
.
Из этих формул видно, что чем чаще делаются взносы, тем больше накопленная сумма. Вторая функция сложного процента показывает, какой будет стоимость серии равновеликих платежей, депонированных в конце каждого из периодических интервалов, по истечении установленного срока.
Фактор фонда возмещения позволяет рассчитать величину периодического платежа, необходимого для накопления нужной суммы по истечении n платежных периодов при заданной ставке процента.
Из формулы будущей стоимости аннуитета можно сделать вывод, что величина каждого платежа (SFF) в случае обычного аннуитета вычисляется следующим образом:
 .
.
В случае авансового возмещения (соответствующего авансовому аннуитету) формула единичного платежа имеет вид:
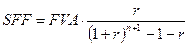 .
.
Из этих формул видно, что чем больше процент, начисляемый на платеж, тем больше величина платежей.
Текущая стоимость денежной единицы – это величина, обратная будущей стоимости денежной единицы (первой функции сложного процента). Текущая стоимость денежной единицы определяется исходя из ее значения, которое должно быть получено в будущем:
 .
.
При более частом накоплении процентов формула принимает вид:
 .
.
Из формул видно, что чем выше частота дисконтирования, тем меньше необходимая сумма текущей стоимости денежной единицы.
Текущая стоимость ( равномерного обычного) аннуитета равна сумме текущих стоимостей всех платежей. Обозначив текущую стоимость k -го платежа через PVk, получаем текущую стоимость равномерного аннуитета:
 .
.
Используя формулу суммы членов геометрической прогрессии, выводится выражение для текущей стоимости аннуитета:
 .
.
Аналогично обычному аннуитету вычисляется текущая стоимость для авансового аннуитета:
 .
.
Из формул видно, что чем больше величина платежа, тем выше текущая суммарная стоимость.
Взнос на амортизацию денежной единицы позволяет определить величину периодического платежа по кредиту (состоящего из части основной суммы долга и процентов за его использование) для его погашения в течение установленного срока. В общеэкономическом смысле амортизация представляет собой процесс погашения долга в течение определенного периода времени. Погашение кредита равномерными платежами предполагает, что текущая стоимость равна первоначальной сумме кредита. Используя формулу текущей стоимости аннуитета, получаем величину периодического платежа – взноса на амортизацию капитала:
 .
.
Используя аналогичные рассуждения, можно получить величину взноса на амортизацию капитала для авансового аннуитета:
 .
.
Каждый равномерный платеж состоит из двух частей:
IAO = IAOпр + IAOкр,
где IAOпр – погашение процентов по кредиту;
IAOкр – погашение кредита (тело кредита).
Таким образом, использование функций финансовой математики в практике оценки стоимости объектов недвижимости повышает ее обоснованность, а также эффективность принятия решений по инвестированию в недвижимость. При этом важнейшей характеристикой изменения ценности денежного потока является норма доходности. Сложность обоснования нормы доходности состоит в том, что она отражает с одной стороны интересы инвестора, а с другой ограничивается внутренними возможностями и внешними факторами.






