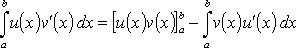
или
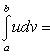
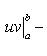
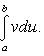
(u, v непрерывно дифференцируемы на интервале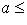 
).
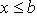Замена переменного (интегрирование подстановкой)
Если функция x = x (u) непрерывно дифференцируема на интервале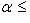 
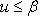, а функция f (x) непрерывна на интервале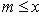 
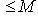, где m - точная нижняя, а M - точная верхняя граница функции x (u) на интервале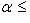 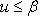, то
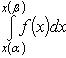
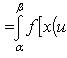
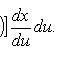
8.Определенный интеграл с переменным верхним пределом.
Пусть на отрезке [ a, b ] задана непрерывная функция f (x), тогда для любого x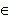 
[ a, b ] существует функция:
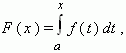
задаваемая интегралом с переменным верхним пределом, стоящим в правой части равенства.
На интеграл с переменным верхним пределом распространяются все правила и свойства определённого интеграла.
| П р и м е р. | Переменная сила на прямолинейном пути изменяется по закону: f (x) = 6 x 2 + 5 при x 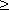 0. По какому закону изменяется работа этой силы?
|
Из определения интеграла с переменным верхним пределом - функции F (x) и известных свойств интеграла следует, что при x 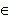[ a, b ]
F' (x) = f (x).
Интеграл с переменным верхним пределом. Значение определённого интеграла не зависит от того, какой буквой обозначена переменная интегрирования: (чтобы убедиться в этом, достаточно выписать интегральные суммы, они совпадают). В этом разделе переменную интегрирования будем обозначать буквой t, а буквой x обозначим верхний предел интегрирования. Будем считать, что верхний предел интеграла может меняться, т.е. что x - переменная, в результате интеграл будет функцией Ф(x) своего верхнего предела:. Легко доказать, что если f (t) интегрируема, то Ф(x) непрерывна, но для нас важнее следующая фундаментальная теорема:
Теорема об интеграле с переменным верхним пределом. Если функция f (t) непрерывна в окрестности точки t = x, то в этой точке функция Ф(x) дифференцируема, и.
Другими словами, производная определённого интеграла от непрерывной функции по верхнему пределу равна значению подынтегральной функции в этом пределе.
Док-во. Дадим верхнему пределу x приращение. Тогда, где c - точка, лежащая между x и (существование такой точки утверждается теоремой о среднем; цифры над знаком равенства - номер применённого свойства определённого интеграла).. Устремим. При этом (c - точка, расположенная между x и). Так как f (t) непрерывна в точке t = x, то. Следовательно, существует, и. Теорема доказана.
Отметим первое важное следствие этой теоремы. По существу, мы доказали, что любая непрерывная функция f (x) имеет первообразную, и эта первообразная определяется формулой. Другим важным следствием этой теоремы является формула Ньютона-Лейбница, или основная формула интегрального исчисления.
9. Несобственные интегралы.
Определенный интеграл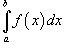 
называется несобственным интегралом, если выполняется, по крайней мере, одно из следующих условий:
· Предел a или b (или оба предела) являются бесконечными;
· Функция f (x) имеет одну или несколько точек разрыва внутри интервала [ a,b ].
