Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул:
1. 
2. 
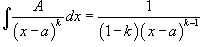
У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат:
где 
Затем применяются следующие формулы:
3. 
4. 
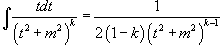
5. 
Интеграл 
может быть вычислен за k шагов с помощью формулы редукции
6. 
4. Интегрирование иррациональных функций.
5. Интегрирование тригонометрических функций.
В данном разделе мы рассмотрим 8 специальных классов интегралов от тригонометрических функций. Для каждого класса применяются определенные преобразования и подстановки, позволяющие получить аналитическое решение.
1. Интегралы вида 
Для решения данных интегралов применяются формулы преобразования произведения тригонометрические функций в сумму или разность:
· 
· 
· 
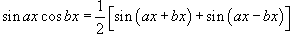
2. Интегралы вида 
Здесь и везде ниже предполагается, что m и n - натуральные числа. Для вычисления таких интегралов используются следующие подстановки и преобразования:
- Если степень косинуса n - нечетная (при этом степень синуса m может быть любой), то используется подстановка
.
- Если степень синуса m - нечетная, то используется подстановка
.
- Если степени m и n - четные, то сначала применяются формулы двойного угла
чтобы понизить синуса или косинуса в подынтегральном выражении. Затем, если необходимо, применяются правила a) или b).
3. Интегралы вида 
Степень подынтегрального выражения в данном интеграле можно понизить с помошью тригонометрического соотношения 
и формулы редукции
4. Интегралы вида 
Здесь степень подынтегрального выражения понижается с помошью соотношения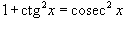 
и формулы редукции
5. Интегралы вида 
Данный тип интеграла упрощается с помощью следующей формулы редукции:
6. Интегралы вида 
Аналогично предыдущим пунктам, интеграл упрощается с помощью формулы
7. Интегралы вида 
- Если степень секанса n - четная, то c помошью соотношения секанс выражается через тангенс. При этом множитель
отделяется и используется для преобразования дифференциала. В результате весь интеграл (включая дифференциал) выражается через функцию tg x.
- Если обе степени n и m - нечетные, то отделяется множитель sec x tg x, необходимый для преобразования дифференциала. Далее весь интеграл выражается через sec x.
- Если степень секанса n - нечетная, а степень тангенса m - четная, то тангенс выражается через секанс с помощью формулы . Затем вычисляются интегралы от секанса.
8. Интегралы вида 
- Если степень косеканса n - четная, то c помошью соотношения
косеканс выражается через котангенс. При этом множитель 
отделяется и используется для преобразования дифференциала. В результате подынтегральная функция и дифференциал выражаются через ctg x.
- Если обе степени n и m - нечетные, то отделяется множитель ctg x cosec x, необходимый для преобразования дифференциала. Далее интеграл выражается через cosec x.
- Если степень косеканса n - нечетная, а степень котангенса m - четная, то котангенс выражается через косеканс с помощью формулы . Далее вычисляются интегралы от косеканса.
6. Определенный интеграл и его свойства. Теорема Ньютона-Лейбница
1.. Определенный интеграл. Формула Ньютона-Лейбница. Теорема о независимости интеграла от выбора первообразной (док-во). Следствие. Теорема существования.
Пусть функция f(х) определена на отрезке и a= x0<x1<…<xn=b — произвольное разбиение этого отрезка на n частей. Сумма вида
где
называется интегральной суммой функции f(x) на отрезке [ а, b ].
Предел интегральной суммы Sn при условии, что число разбиений отрезка [ а, b ] неограниченно увеличивается,, а наибольшая из разностей (длин частичных отрезков разбиения) стремится к нулю, называется определенным интегралом от функции f(х) на отрезке [ а, b ] и обозначается символом
т.е.
где f(x) — подынтегральная функция;
а — нижний предел интегрирования;
b - верхний предел интегрирования.
Формулой Ньютона - Лейбница называется равенство вида:
При этом предполагается, что подынтегральная функция f(x) непрерывна при всех значениях x, удовлетворяющих условиям
a £ x £ b.
