Определение первообразной и неопределенного интеграла
Функция F (x) называется первообразной функции f (x), если
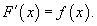
Множество всех первообразных некоторой функции f (x) называется неопределенным интегралом функции f (x) и обозначается как
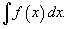
Таким образом, если F - некоторая частная первообразная, то справедливо выражение

где С - произвольная постоянная.
Свойства неопределенного интеграла
В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f,
а, k, C - постоянные величины.
· 
· 
· 
· 
Таблица интегралов
В формулах ниже предполагается, что a, p (p ≠ 1), C - действительные постоянные, b - основание показа
тельной функции (b ≠ 1, b > 0).

| 
|
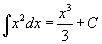
| 
|

| 
|

| 
|
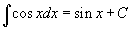
| 
|

| 
|

| 
|

| 
|

| 
|
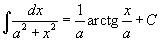
| 
|

| 
|

| 
|

| 
|
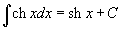
| 
|

| 
|

| 
|
2 Методы интегрирования функций
Метод непосредственного интегрирования.
Осуществляется с использованием свойств интеграла и сведением интеграла к табличному.
Примеры:
1)
∫(5cos(x)+2−3 x 2+ x 1−4 x 2+1) dx =5∫cos(x) dx +2∫ dx −3∫ x 2 dx +∫ xdx −4∫ dxx 2+1= =5sin(x)+2 x − x 3+ln∣ x ∣−4 arctg (x)+ C.






