1) 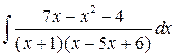 2)
2) 
3)  4)
4) 
5) 
Решение:
1) 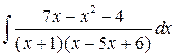
Подынтигральная функция представляет собой рациональную дробь. Разложим ее знаменатель на множители:  . В разложении правильной дроби на простейшие каждому множителю знаменателя вида
. В разложении правильной дроби на простейшие каждому множителю знаменателя вида  соответствует слагаемое
соответствует слагаемое 
Поэтому в данном случае имеем


Приведя правую часть последнего равенства к общему знаменателю и приравняв числители дробей, получим тождество
 ,
,
Коэффициенты А, В, С определим с помощью метода частных значений

откуда А=-1, В=-2, С=2. Подставив найденные коэффициенты в разложении подынтегральной функции на простейшие дроби, получим

2) 

Ответим, что для нахождения коэффициентов мы использовали комбинированный метод: метод частных значений и метод неопределенных коэффициентов.

4) 
Подынтегральной функцией является правильная дробь, разложение которой в сумму простейших имеет вид:

Приводя правую часть к общему знаменателю, получаем:

Приравняем коэффициенты при одинаковых степенях х, что приведет к линейной системе относительно A,B,C,D,E:
x 4: A + B = 0
x ³: -2 B + C = 0
x ²: 2 A + B – 2 C + D = 2
x: -2 B + C – 2 D + E = 2
x 0: A – 2 C – 2 E = 13.
Отсюда A = 1, B = -1, C = -2, D = -3, E = -4. Следовательно,
 , где
, где



 Таким образом, окончательный результат имеет вид:
Таким образом, окончательный результат имеет вид:

5) 
Так как подынтегральная функция является неправильной дробью, то путем деления числителя на знаменатель можно представить ее в виде суммы целого многочлена и правильной рациональной дроби:







