Формула интегрирования по частям: 
Для применения этой формулы нужно подынтегральное выражение представить в виде произведения двух множителей:  и
и  ; за
; за  всегда выбираются выражения содержащее
всегда выбираются выражения содержащее  , из которого интегрирование можно найти
, из которого интегрирование можно найти  ; за
; за  обычно принимается функция, которая при дифференцировании упрощается (например:
обычно принимается функция, которая при дифференцировании упрощается (например:  ,
, 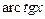 ,
,  ,
,  ,
,  ,
,  ).
).
Пример 1. Найти интегралы:
1)  2)
2)  3)
3)  4)
4) 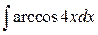
5)  6)
6)  7)
7) 
Решение:



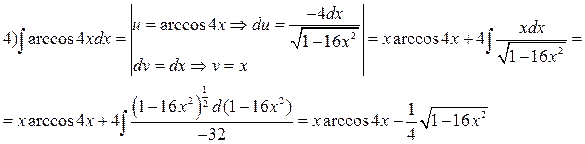
5) 


Задачи для самостоятельной аудиторной и внеаудиторной работы
1)  Ответ:
Ответ: 
2)  Ответ:
Ответ: 
3)  Ответ:
Ответ: 
4)  Ответ:
Ответ: 
5)  Ответ:
Ответ: 
6)  Ответ:
Ответ: 
7)  Ответ:
Ответ: 
8)  Ответ:
Ответ: 
9)  Ответ:
Ответ: 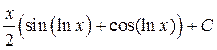
10) 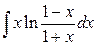 Ответ:
Ответ: 
11)  Ответ:
Ответ: 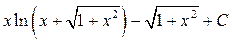
12)  Ответ:
Ответ: 
13) 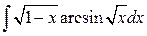 Ответ:
Ответ: 
14)  Ответ:
Ответ: 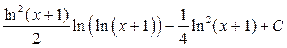
Интегрирование простейших иррациональных функций.


где R-рациональная функция своих аргументов
m1,n1,m2,n2,… целые числа, вычисляются с помощью подстановки 
где S-общий знаменатель дробей: 






