Если рациональная дробь 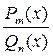 является неправильной, то есть т ≥ п, то ее можно представить в виде суммы
является неправильной, то есть т ≥ п, то ее можно представить в виде суммы  где Мт-п и Rr – многочлены степеней т-п ≥ 0 и r, причем r < n. Разложение правильной дроби
где Мт-п и Rr – многочлены степеней т-п ≥ 0 и r, причем r < n. Разложение правильной дроби 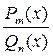 в сумму простейших имеет вид:
в сумму простейших имеет вид: 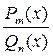 = =
= = 
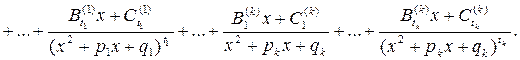
При этом каждая из простейших дробей, стоящих в правой части равенства, интегрируется в квадратурах.
Таким образом, для того, чтобы проинтегрировать рациональную дробь, необходимо в случае, если она является неправильной, выделить целую часть, затем разложить знаменатель оставшейся правильной дроби на множители степени не выше второй и представить эту дробь в виде суммы простейших дробей, вычислив коэффициенты их числителей с помощью метода неопределенных коэффициентов или метода частных значений.






