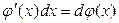1) 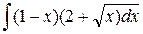 ответ:
ответ: 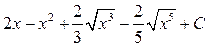
2)  ответ:
ответ: 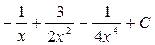
3)  ответ:
ответ: 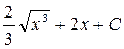
4) 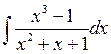 ответ:
ответ: 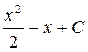
5) 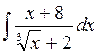 ответ:
ответ: 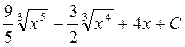
6)  ответ:
ответ: 

7)  ответ:
ответ: 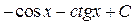
8) 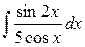 ответ:
ответ: 
9)  ответ:
ответ: 
10) 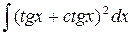 ответ:
ответ: 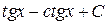
11)  ответ:
ответ: 
12) 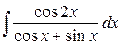 ответ:
ответ: 
13) 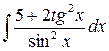 ответ:
ответ: 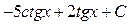
14)  ответ:
ответ: 
15) 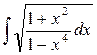 ответ: arcsin x + C
ответ: arcsin x + C
16)  ответ:
ответ: 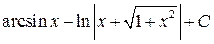
17) 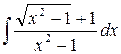 ответ: ln
ответ: ln 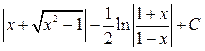
18) 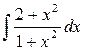 ответ: x + arctg x + C
ответ: x + arctg x + C
19) 
 ответ:
ответ: 
20)  ответ: ln
ответ: ln 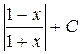
21) 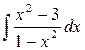 ответ:
ответ: 
22)  ответ:
ответ: 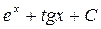
23) 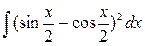 ответ: x + cosx + C
ответ: x + cosx + C
24) 
 ответ:
ответ: 
Метод подведения под знак дифференциала.
Метод внесения функции под знак дифференциала состоит в том, что новая переменная не выписывается явно. Для подынтегрального выражения выделяется некоторая функция 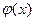 , дифференциал от которой
, дифференциал от которой  входит составной частью в подынтегральное выражение
входит составной частью в подынтегральное выражение  , т.е.
, т.е.  . Тогда исходный интеграл преобразуется к виду:
. Тогда исходный интеграл преобразуется к виду:
 .
.
Полученный интеграл может оказаться существенно проще, а в некоторых случаях свестись к табличному.
Отметим ряд преобразований дифференциала, полезных для дальнейшего:
1)  где b-постоянная величина;
где b-постоянная величина;
2)  где константа
где константа  ;
;
3)  4) xdx =
4) xdx = 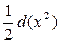 5) sinxdx=-d(cosx)
5) sinxdx=-d(cosx)
6)  7)
7) 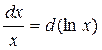 8)
8) 
9) 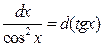 10)
10) 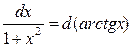 11)
11) 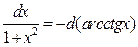
12)  13)
13) 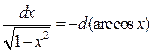 14)
14) 
Вообще,