Формула Бернулли удобна для вычислений лишь при сравнительно небольшом числе испытаний n. При больших значениях n и малых рпользоваться этой формулой неудобно. Чаще всего в этих случаях используют формулу Пуассона. Эта формула определяется теоремой Пуассона.
Теорема 1. Если вероятность р наступления события А в каждом испытании постоянна и мала, а число независимых испытаний и достаточно велико, то вероятность того, что событие А наступит m раз, приближенно равна
 (4)
(4)
где l=np
Пример. Предприятие изготовило и отправило заказчику 100 000 бутылок пива. Вероятность того, что бутылка может оказаться битой, равна 0,0001. Найти вероятности того, что в отправленной партии бу- дет три и пять битых бутылок.
РЕШЕНИЕ. Дано: n = 100 000, р = 0,0001, и = 3 (т = 5). Находим Х = пр = 10.
Воспользуемся формулой Пуассона:



ЗАДАЧА 1. В результате обследования были выделены семьи, имеющие по 4 ребенка. Считая вероятности появления мальчика и девочки в семье равными, определить вероятности появления в ней:
А) 1 мальчика;
Б) 2 мальчиков.
РЕШЕНИЕ. вероятность появления мальчика или девочки равна р=1/2. Вероятность появления мальчика в семье, имеющей 4 детей, находится по формуле Бернулли:

Вероятность появления в семье 2 мальчиков равна
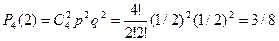
ЗАДАЧА 2. В новом микрорайоне поставлено 10000 кодовых замков на входных дверях домов. Вероятность выхода из строя одного замка в течение месяца равна а) 0,0002; б) 0,001. Найти вероятность того, что за месяц откажут 2, 3 и 5 замков.
РЕШЕНИЕ. а) Используем формулу Пуассона
 , l=np
, l=np
В нашем случае l=10000*0,0002=2,
Тогда Р10000(2)=22е-2/2!=0,27;
Р10000(3)=23е-2/3!=0,18; (е-2=1/(2,71*2,71)=1/7,34)
Р10000(5)=25е-2/5!=0,36;
Б) е-10=0,000045
ЛИТЕРАТУРА:
1. Информатика и математика для юристов.// Под ред. Х.А.Андриашина. – М.: ЮНИТИ, 2003.
2. Основы информатики и математики для юристов. // Богатов и Богатов. Учебное пособие для вузов.
3. Козлов В.Н. Математика и информатика. //Учебное пособие. СПб: Питер, 2004.
4. Основы информатики. В.З. Аладьев и др.// Учебное пособие.-1999.






