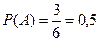
Статистическое определение вероятности связано с понятием относительной частоты появления события А в опытах. Относительная частота появления события А вычисляется по формуле
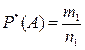 (2)
(2)
где m1, — число появлений события А в серии из n1, опытов (испытаний).
Вероятностью события А называется число, относительно которого стабилизируется (устанавливается) относительная частота Р'(А) при не- ограниченном увеличении числа опытов.
В практических задачах за вероятность события А принимается относительная частота Р*(А) при достаточно большом числе испытаний.
Из определений вероятности события А следует, что всегда выполняются неравенства
0< P(A) <1.
Для того чтобы вычислить вероятность события на основе формулы (1), часто используют формулы комбинаторики.
Для вычисления числа благоприятствующих рассматриваемому событию исходов или общего числа элементарных исходов широко используются формулы комбинаторики, по которым находят число благоприятствующих исходов и общее число возможных исходов.
Если комбинации берутся из всех n элементов и отличаются только порядком следования элементов, то они называются перестановка Их число равно
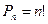
Задача 1. Сколько четных пятизначных чисел можно составить из цифр 1, 2, 3, 4 и 5 так, чтобы ни одна из цифр не повторялась?
Решение. Количество пятизначных чисел равно числу перестановок из пяти элементов:
Р5=5!=1*2*3*4*5=120
Из данных цифр можно составить 120 чисел, причем нас интересуют только те из них, которые оканчиваются на 2 или на 4. Зафиксируем цифру 2 на последней позиции, тогда первые 4 позиции могут занимать цифры 1, 3, 4 и 5. Поскольку Р4=4!=24, то чисел, оканчивающихся на 2 из данных пяти цифр можно составить 24. Легко видеть, что столько же чисел будет оканчиваться цифрой 4. Значит, из цифр 1, 2, 3, 4 и 5 можно составить (без повторений цифр) 48 четных чисел
Если составляются такие комбинации из nэлементов по т, которые отличаются друг от друга только составом элементов, то они называю сочетаниями. Общее число сочетаний из nэлементов по т определял по формуле

Задача 2. Группа студентов из 25 человек выбирает трех делегатов на конференцию. Сколькими способами могут быть проведены эти выборы?
Используя формулу, можно решить задачу 1. Имеем

Если комбинации отличаются не только составом элементов, но и порядком их следования, то они называются размещениями. Их число находится по формуле

Задача 3. Группа студентов из 25 человек выбирает старосту, профорга и культорга. Сколькими способами могут быть проведены эти выборы?
Решение. Эта задача похожа на задачу 1, но отличается от нее тем, что нужно не просто выбрать троих из 25, а и распределить их по должностям. Другими словами, на каждое выбранное подмножество (сочетание) из 25 по 3 приходится еще 3! = 6 перестановок. Поэтому результат решения задачи в P3=6 раз больше, чем С253, т.е. равен
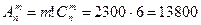
Пример. Известно, что в поступившей партии из 30 швейных машинок 10 имеют внутренний дефект. Определить вероятность того, ч из пяти наудачу взятых машинок три окажутся бездефектными.
Р е ш е н и е. Введем следующие обозначения: N — общее число машинок, n — число бездефектных машинок, m — число отобранных партию машинок, k — число бездефектных машинок в отобранной партии.
Общее число комбинаций по m машинок, т. е. общее число возможных исходов, будет равно числу сочетаний из N элементов по m, т. е, 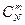 . Но в каждой отобранной комбинации должно содержаться по три бездефектные машинки. Число таких комбинаций равно числу сочетаний из nэлементов по k, т. е.
. Но в каждой отобранной комбинации должно содержаться по три бездефектные машинки. Число таких комбинаций равно числу сочетаний из nэлементов по k, т. е. 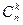 .
.
Оставшиеся дефектные машинки (элементы) тоже образуют множество комбинаций, число которых равно числу сочетаний из N — n элементов по m — k, т. е. 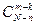 .
.
Это значит, что общее число благоприятствующих исходов определяется произведением 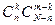 . Откуда
. Откуда
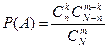
Подставив в эту формулу численные значения данного примера, получим
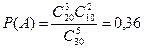
1. В магазин поступило 30 холодильников, пять из имеют заводской дефект. Случайным образом выбирает один холодильник. Какова вероятность того, что он будет дефекта?
2. В коробке находится шесть одинаковых по форм близких по диаметру сверл. Случайным образом сверла из каются из коробки. Какова вероятность того, что сверла влекутся в порядке возрастания их диаметра?
3. Комиссия по качеству раз в месяц проверяет качество продуктов в двух из 30 магазинов, среди которых находятся и два известных вам магазина. Какова вероятность того, что в течение месяца они оба будут проверены?
4. На станцию прибыли 10 вагонов разной продукции. Вагоны помечены номерами от одного до десяти. Найти вероятность того, что среди пяти выбранных для контрольного вскрытия вагонов окажутся вагоны с номерами 2 и 5?
РЕШЕНИЕ: Общее число возможных комбинаций для контрольного вскрытия равно числу сочетаний из 10 по 5, т.е. 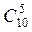
Число исходов, благоприятствующих данному событию, будет равно числу таких комбинаций, в которых две цифры будут 2 и 5, а остальные будут составлять сочетания, число которых равно С38. Тогда искомая вероятность найдется по формуле
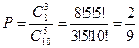
5. Из 20 акционерных обществ (АО) четыре являются банкротами. Гражданин приобрел по одной акции шести АО. Какова вероятность того, что среди купленных акций две окажутся акциями банкротов?
РЕШЕНИЕ. Общее число комбинаций выбора АО равно числу сочетаний из 20 по 6, т.е. С206. Число благоприятствующих исходов определяется как произведение  , где первый сомножитель указывает число комбинаций выбора АО-банкротов из 4. Но с каждой такой комбинацией могут встретиться Ао, не являющиеся банкротами. Число комбинаций таких АО будет С416. Поэтому искомая вероятность запишется в виде
, где первый сомножитель указывает число комбинаций выбора АО-банкротов из 4. Но с каждой такой комбинацией могут встретиться Ао, не являющиеся банкротами. Число комбинаций таких АО будет С416. Поэтому искомая вероятность запишется в виде
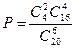 , т.е. Р=0,28.
, т.е. Р=0,28.






