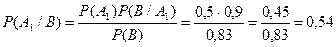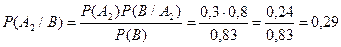Предположим, что событие В может произойти только с одним из несовместных событий А1,А2..., Аn. Например, в магазин поступает одна и та же продукция от трех предприятий и в разном количестве. Вероятность выпуска некачественной продукции на этих предприятиях различна. Случайным образом отбирается одно из изделий. Требуется определить вероятность того, что это изделие некачественное (событие В). Здесь события А1,А2..., Аn — это выбор изделия из продукции соответствующего предприятия.
В этом случае вероятность события В можно рассматривать как сумму произведений событий
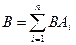
По теореме сложения несовместных событий (см. теорему 1) получаем:
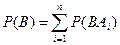
Используя теорему умножения вероятностей, находим
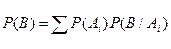 (1)
(1)
Формула (1) носит название формулы полной вероятности.
Пример. Для рассмотренного выше случая с поступлением товара в магазин от трех предприятий зададим численные значения. Пусть от первого предприятия поступило 20 изделий, от второго — 10 и от третьего — 70. Вероятности некачественного изготовления изделия на предприятиях соответственно равны 0,02; 0,03и 0,05.
Определить вероятность получения некачественного изделия.
РЕШЕНИЕ. Вероятности событий А1,А2..., Аn будут соответственно Р(А,) = 0,2; Р(А,) = 0,1; Р(А,) = 0,7.Используя формулу (3.1), находим
P(B) = 0,2 0,02 + 0,1 0,03 + 0,7 0,05 = 0,042.
3.2. Формула Байеса
Пусть событие В происходит одновременно с одним из n несовместных событий А1,А2..., Аn. Требуется найти вероятность события Аi, если известно, что событие В произошло.
На основании теоремы о вероятности произведения двух событий (см. теорему 2)
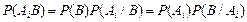
откуда
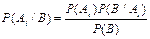
или
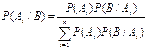 (2)
(2)
Формула (2) носит название формулы Байеса.
Пример. Три организации представили в контрольное управление счета для выборочной проверки: первая — 15 счетов, вторая — 10, третья — 25. Вероятности правильного оформления счетов у этих организаций соответственно таковы: 0,9; 0,8; 0,85. Был выбран один счет, и он оказался правильным. Определить вероятность того, что этот счет при- надлежит второй организации.
РЕШЕНИЕ.. Пусть А1,А2..., Аn — события выбора счета соответственно у первой, второй и третьей организации. Вероятности этих событий таковы:
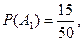
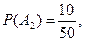
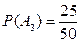
По формуле полной вероятности (см. формулу (1)) определяем вероятность выбора правильно оформленного счета:
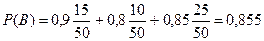
По формуле Байеса находим искомую вероятность:
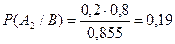
ЗАДАЧА. На автозавод поступили двигатели от 3 моторных заводов. От первого завода поступило 10 двигателей, от второго – 6 и от третьего – 4 двигателя. Вероятности безотказной работы этих двигателей в течение гарантийного срока соответственно равны 0,9; 0,8; 0,7.
Какова вероятность того, что:
А) установленный на машине двигатель будет работать без дефектов в течение гарантийного срока;
Б) проработавший без дефекта двигатель изготовлен на первом заводе, на втором заводе?
РЕШЕНИЕ. Обозначим через А1, А2, А3 события установки на автомашину двигателей, изготовленных соответственно на первом, втором или третьем моторных заводах. Вероятности этих событий таковы:
Р(А1)=0,5; Р(А2)=0,3; Р(А3)=0,2.
А) Вероятность того, что наугад взятый двигатель проработает без деффектов, найдем по формуле полной вероятности:
P(B)=P(A1)P(B/A1)+P(A2)P(B/A2)+P(A3)P(B/A3)=0,5*0,9+0,3*0,8+0,2*0,7=0,83
Б) Если двигатель проработал без дефектов гарантированный срок, то вероятности того, что он изготовлен на первом, на втором заводах, найдем по формуле Байеса: