ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
ВЕРОЯТНОСТЬ СОБЫТИЯ
Случайные события
В областях человеческой деятельности или в природе, постоянно приходится иметь дело с событиями, которые невозможно точно предсказать. Так, объем продаж товара за висит от спроса, который может существенно изменяться, и от ряда Других факторов, учесть которые практически нереально. Поэтому при организации производства и осуществлении продаж приходится прогнозировать исход такой деятельности либо на основе собственного или чужого опыта, либо на основе интуиции, которая в значительной степени тоже опирается на опытные данные. Чтобы каким-то образом оценить событие, необходимо учесть или специально организовать условия, в которых оно происходит. Выполнение определенных условий или действий для выявления рассматривaeмoгo события носит название опыта или эксперимента. Событие называется случайным, если в результате опыта оно может ибо произойти, либо не произойти. Событие называется достоверным, если оно обязательно появляется результате данного опыта, и невозможным, если оно не может появиться в этом опыте. Например, выпадение снега в Москве 30 ноября является случайным событием. Ежедневный восход Солнца можно считать достоверным событием, а выпадение снега на экваторе — невозможным событием. Одной из главных задач в теории вероятностей является задача определения количественной меры возможности появления события.
Алгебра событий
События называются несовместными, если они вместе не могут наблюдаться в одном и том же опыте. Так, продажа двух и трех автомашин в одном магазине одновременно — это два несовместных события.
Суммой событий А1,А2,..., Аn называется событие, состоящее в появлении хотя бы одного из этих событий: 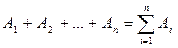
В качестве примера суммы событий можно назвать продажу в магазине хотя бы одного из двух товаров.
Произведением событий А1,А2,..., Аn называется событие, состоящее в одновременном появлении всех этих событий:

Событие, состоящее в одновременной продаже в магазине двух товаров, является произведением событий А, и А, где А, — продажа одного товара, А, — продажа другого товара.
События В1, В2,..., Вk образуют полную группу событий, если хотя бы одно из них обязательно произойдет в опыте.
Пример. В порту имеется два причала для приема судов. Можно рассмотреть три события: В1 — отсутствие судов у причалов, В2 — присутствие одного судна у одного из причалов, В3 — присутствие двух судов у двух причалов. Эти три события образуют полную группу.
Противоположными называются два единственно возможных события, образующих полную группу.
Если одно из двух противоположных событий обозначить через А, то другое обычно обозначают через  или
или 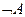 .
.
1.2. Классическое и статистическое определения вероятности события
Каждый из равновозможных результатов испытаний (опытов) называется элементарным исходом. Их обычно обозначают буквами 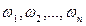 . Например,подбрасывая игральную кость, можно получить шесть элементарных исходов (по числу очков на гранях). Из элементарных исходов можно составить более сложное событие. Так, событие выпадения четного числа очков определяется тремя исходами: 2, 4, 6.
. Например,подбрасывая игральную кость, можно получить шесть элементарных исходов (по числу очков на гранях). Из элементарных исходов можно составить более сложное событие. Так, событие выпадения четного числа очков определяется тремя исходами: 2, 4, 6.
Количественной мерой возможности появления рассматриваемого события является вероятность. Наиболее широкое распространение получили два определения вероятности события: классическое и статистическое.
классическое определение вероятности связано с понятием благоприятствующего исхода. Исход называется благоприятствующим данному событию, если его появление влечет за собой наступление этого события.
Вероятность события А равна отношению числа благоприятствующих исходов к общему числу возможных исходов:
 (1)
(1)
где т — число благоприятствующих событию А исходов; n — общее число возможных исходов.
Рассматриваемое событие — четное число очков на выпавшей грани имеет три благоприятствующих исхода. В данном случае известно и общее количество возможных исходов. Значит, здесь можно использовать классическое определение вероятности события.






