Суперпозиція функцій f1…fn це функція F отримана за допомогою підстановки функцій одна в одну в якості аргументу и перейменування даного аргументу. Формулою називається вираз який описує дану суперпозицію.
Поняття суперпозиції дуже важливе в матлогіці. Нехай є множина (скінченна чи безмежна) функцій {f1…fn…}=å. Символи стартових змінних будемо називати «0» глибини. Тобто стартові аргументи х1…хn… - формули «0» глибини. Формула F має глибину «к+1» тоді коли F= fi(F1,…,Fni), і якщо F1,…,Fni мають «к» глибину.
Формули (аргументи функції F) F1,…,Fni називаються підформулами F. fi – називаються зовнішньою або ж головною операцією формули F.
Такі назви використовуються для всіх виразів, що входять в суперпозицію. Наприклад f1(x1,x2)– формула «1» глибини, f2(f1 (x1,x2))– формула «2» глибини і т.д.
Приклад: нехай f1 – диз’юнкція f2– кон’юнкція, f3 – додавання по модулю 2.
Тоді:
f3(f1(х1,х2), f2(х1, f3(х1,х2)))=(х3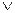 
х1) Å(х1 
(х1 Åх2))
Форма запису функцій, коли використовуються символи ù, , ,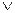Å,®,~, дії між аргументами називається інфіксною.
Принцип обчислення значення функції при заданих значеннях аргументів.
Нехай х1=1, х2=1, х3=0
Тоді:
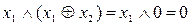
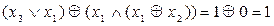
Зрозуміло, що усі обчислення, при невеликому числі аргументів, можна представити за допомогою таблиці істинності.
Ще раз звертаємо увагу, що довільні функції матлогіки можна виразити через інші з глибиною 1 або 2. Наприклад штрих Шеффера
х1| х2= 
або ж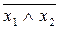 
.
Функцію “стрілка Пірса”
х1¯х2=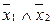 
або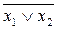 
.
Формули, які по різному представляють одну і ту ж функцію називаються еквівалентними або ж рівносильними.
Щоб перевірити чи є дані представлення функцій еквівалентними необхідно порівняти їх таблиці істинності.
Наприклад: =
| 
| 
| 
|
|
|
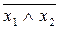
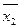
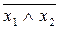
Останні два стовпці стверджують еквівалентність відповідних функцій.
