1а.  1б.
1б. 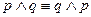
2а.  2б.
2б. 
3а.  3б.
3б. 
4а.  4б.
4б. 
5а.  5б.
5б. 
6а. 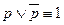 6б.
6б. 
7а.  7б.
7б. 
8а.  8б.
8б. 
9а.  9б.
9б. 
Приклад 1. Довести еквівалентності 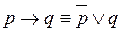 ;
;  , тобто довести, що імплікація (®) виражається через ù, Ú. Еквівалентність через ù та Ú, Ù.
, тобто довести, що імплікація (®) виражається через ù, Ú. Еквівалентність через ù та Ú, Ù.
Розв‘язок. Складаємо таблицю істинності

| 
| 
| 
| 
| 
| 
| 
|
 1 1
|

Приклад 2. Довести, що формула  є тавтологією. Доведемо за допомогою таблиці істинності
є тавтологією. Доведемо за допомогою таблиці істинності

| 
| 
| 
| 
| 
|

Скористаємось законами алгебри логіки. 
Приклад 3. Довести, що формула  є тавтологією.
є тавтологією.
Таблиця істинності

| 
| 
| 
| 
| 
| 
| 
| ||
| |||||||||
Приклад 4. Доведемо, що  є тавтологія.
є тавтологія.
Таблиця істинності

| 
| 
| 
| 
| 
| 
|

Приклад 5. Довести, що якщо 
 ,
,  то
то  .
.
На основі тавтології 
маємо,  .
.
Тоді  ; тоді
; тоді  . А оскільки
. А оскільки  то і
то і  . То твердження
. То твердження  істинне, так-як базується на початкових даних.
істинне, так-як базується на початкових даних.
Як вже відмічалось раніше, математична логіка розглядає положення, твердження, які можуть не мати фізичного змісту.
Наприклад. Задача 5.

Дано хороша погода  киця іде гуляти, киця іде гуляти
киця іде гуляти, киця іде гуляти  киця здорова. Отже хороша погода
киця здорова. Отже хороша погода  киця здорова. Таке твердження немає логічного змісту.
киця здорова. Таке твердження немає логічного змісту.






