Паралельні та послідовні з’єднання розмикаючих і замикаючих контактів називається релейно контактною схемою (РКС).
Є два типи контактів замикаючий і розмикаючий. Перший – контакт, який проводить струм коли його натискають, розмикаючий контакт, навпаки, проводить струм у не натиснутому стані.
ненатиснуті контакти
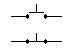замикаючий (зараз схема розімкнута)
розмикаючий (зараз схема зімкнута)
натиснуті контакти
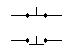замикаючий (зараз схема зімкнута)
розмикаючий (зараз схема ро зімкнута)
Але ми надалі будемо позначати їх так:
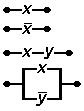замикаючий контакт
розмикаючий контакт
послідовне з’єднання
паралельне з’єднання
Замикаючі контакти позначаємо Х, а розмикаючі 
, тобто в тому положенні, в якому вони пропускають струм.
Розглянемо таку просту РКС.
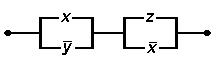
Зауважимо, що перемикачі Х і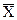 
не пропускають струм одночасно. Дана РКС проводить струм коли хоча б один з контактів Х або 
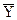замкнутий і одночасно замкнутий хоча б один з контактів Z або 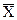. Для отриманого висловлення(попереднього речення) будуємо 
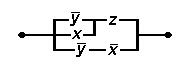схему, яка матиме вигляд:
У правій частині маємо рівносильну формулу, за якою можна скласти РКС, яка буде з’єднаною тоді і тільки тоді коли буде з’єднаною дана РКС.
Дуже часто доводиться мати справу з великими і громіздкими РКС, які потрібно спростити. Для цього складають логічну формулу, яка відповідає цій РКС, знаходять ДДНФ цієї формули і мінімізують її методом склеювання або за допомогою карт Карно. За мінімізованою ДДНФ будуємо нову РКС, яка зазвичай має менше перемикачів, ніж початкова.
„Те, що написано на початку цього розділу – безсовісна брехня”
[1] Наведене означення, як і ряд інших, не є строгим означенням, однак сподіваюся, що воно буде зрозумілим читачу.
