Серед логічних операцій найбільш вживаними в математичній логіці є кон’юнкція, диз’юнкція та заперечення. Неважко переконатись (як саме?) в справедливості таких властивостей цих операцій (властивості запишемо у вигляді таблиці):
| Властивість | Кон’юнкція | Диз’юнкція |
| Комутативність | АВ º ВА | 
|
| Асоціативність | (АВ)С º А(ВС) | 
|
| Дистрибутивність | 
| 
|
| Закони де-Моргана | 
| 
|
| Індемпотентність | АА º А | 
|
| Закони поглинання | 
| 
|
| А×1 º А |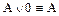 
| |
| А×0 º 0 | 
| |
| Закон подвійного заперечення | 
|
Завдання. Перевірте справедливість законів де Моргана.
Придивіться до цієї таблиці, спробуйте виявити якісь закономірності, особливості операцій. Зверніть увагу на те, що формули кожного стовпчика можна отримати із формул іншого стовпчика заміною кон’юнкції на диз’юнкцію, 0 на 1 і навпаки.
Логічна формула 
називається двоїстою до формули А, якщо вона отримана з А шляхом заміни кон’юнкції на диз’юнкцію, 0 на 1 і навпаки.
Теорема. Якщо А º В, то і А* º В*.
Завдання. Перевірте рівносильність формул:
.
У випадку рівносильності запишіть рівносильні двоїсті формули.
Завдання. Придумайте дві рівносильні формули, які містять лише кон’юнкцію, диз’юнкцію та заперечення. Для них запишіть двоїсті та переконайтесь в справедливості приведеної вище теореми для Вашого випадку.
