Задача 1.а. Розв’язати систему лінійних рівнянь (варіанти 1-30) трьома способами: а) методом Гаусса; б) за формулами Крамера; в) методом оберненої матриці (з цією метою ввести необхідні позначення і записати систему у вигляді матричного рівняння, розв’язком якого буде стовпець невідомих; для перевірки обчислень оберненої матриці скористатися її означенням).
| 1. | -3x + 2y - 4z = 15; 4x - 5y + 3z = -27; 5x + 3y - 4z = 28. | 2. | -4x - 3y + 2z = -12; -5x - 4y + 5z = -22; -2x + 3y - z = -9. |
| 3. | 3x + 2y + 4z = -9; 2x - 2y + 5z = 2; 4x - y + 4z = -11. | 4. | 4x + 4y + z = -27; -5x + 5y + 4z = -1; 2x - y - 3z = -5. |
| 5. | 4x + y - 3z = -34; -5x - 2y + 2z = 41; 2x - 4y - 3z = 1. | 6. | 5x + 4y + 4z = -3; -5x - 3y + 4z = -1; 5x - 2y - 2z = -21. |
| 7. | 4x + 4y - 4z = 4; -5x - y + 3z = 11; -5x + 3y - 2z = 21. | 8. | 2x - 5y - 5z = -1; -5x - 3y + z = 26; 5x - 2y - 2z = -13. |
| 9. | 3x + 3y + 3z = -27; -2x - 5y + 5z = -2; -2x + 2y + z = -17. | 10. | 4x + 4y - 5z = -17; -5x - 3y + 2z = -4; -4x + 4y + 3z = -9. |
| 11. | 4x - 2y - 3z = -13; 2x + 5y + 3z = -32; -4x - 2y - 5z = 25. | 12. | 3x - y + 5z = -10; 4x + 5y + 4z = -19; 4x + 4y - 2z = 14. |
| 13. | 3x - 4y - 3z = 21; -5x + 5y - 2z = -44; 3x - 2y + z = 23. | 14. | 5x + 2y - 3z = -37; -5x + 2y + z = 21; 2x + 4y + z = -20. |
| 15. | 3x - 2y + 4z = 31; 4x + 2y - 2z = 10; -3x - 5y + 2z = 1. | 16. | -3x - y - 5z = 1; -4x + 3y + 5z = 16; 3x - 5y - 4z = -7. |
| 17. | 5x - 3y - 2z = -2; 2x + 5y - 2z = 29; 5x + 5y + z = 41. | 18. | -3x + 4y + z = 1; -4x - y - 5z = 33; 2x - 4y - 3z = 9. |
| 19. | 3x - 2y + 3z = -15; -3x - 3y - 4z = 5; -4x - 4y - 3z = -5. | 20. | -3x + y - 5z = 2; 4x + 5y - 5z = 7; 2x - 3y + 2z = 12. |
| 21. | -5x - y - 4z = 44; 2x + 3y - 4z = 13; -2x + 5y + 2z = 5. | 22. | 2x + 3y - 4z = -3; 5x - 5y + 5z = 40; 2x + y + 5z = 31. |
| 23. | -3x - 5y + 3z = 31; -5x + 2y + 2z = 3; -3x + 3y + 5z = -11. | 24. | -5x - 2y - 4z = -2; -5x - 4y - 3z = 1; 4x + 3y + 4z = -2. |
| 25. | 3x - 5y + z = -17; 2x - 5y + 3z = -6; 3x - 4y - 2z = -25. | 26. | 4x - y + 2z = 18; 2x - 3y + 3z = 8; -4x - y - 5z = -28. |
| 27. | 3x - 3y + 4z = 8; 2x - 3y - 3z = 33; 3x - 3y - 2z = 32. | 28. | -2x + 3y - 3z = 2; -3x - 2y + 5z = 19; 5x + 3y - 4z = -27. |
| 29. | -2x + 5y - 2z = -24; -4x - 2y + 3z = 7; 2x + y - 5z = -7. | 30. | 2x - 2y - z = 3; 3x + 4y - 5z = 1; -5x - 4y + 3z = -15. |
Задача 1.б. Дослідити СЛР на сумісність і знайти розв’язки, якщо вони існують.
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
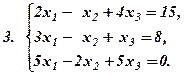
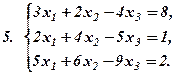
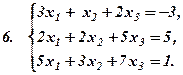
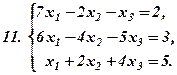
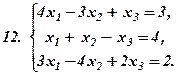
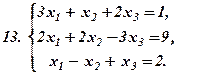
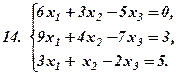
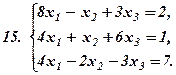
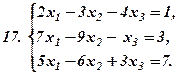
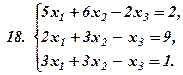
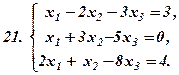
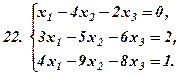
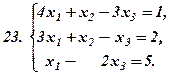
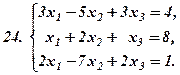
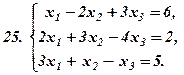
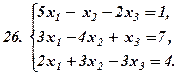
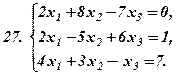
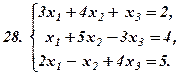
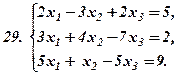
Задача 1.в. Розв’язати систему лінійних зшвнянь методом Гаусса.
| Варіант 1 3.681X1 - 4.425X2 + 7.642X3 - 3.463X4= 9.313 -4.142X1 - 2.628X2 - 4.196X3 + 5.170X4= 9.533 -2.725X1 - 6.801X2 - 2.162X3 + 4.207X4= -0.615 9.801X1 - 1.434X2 - 8.958X3 - 9.868X4= -5.260 |
| Варіант 2 -3.958X1 + 1.512X2 - 8.600X3 + 0.096X4= 3.251 -4.398X1 - 6.249X2 - 5.512X3 + 1.210X4= -0.945 -3.476X1 - 4.553X2 - 7.078X3 + 9.401X4= 5.191 -7.794X1 + 9.536X2 - 5.179X3 + 6.712X4= -7.144 |
| Варіант 3 1.917X1 + 1.231X2 - 3.034X3 + 7.783X4= -0.543 -6.542X1 - 1.236X2 - 8.218X3 - 6.194X4= -2.751 6.008X1 - 8.470X2 - 8.697X3 - 8.897X4= -8.304 6.378X1 - 4.637X2 + 4.292X3 - 7.115X4= -2.036 |
| Варіант 4 -8.201X1 - 9.515X2 + 4.378X3 - 0.351X4= -5.143 -5.534X1 - 2.996X2 - 1.726X3 - 9.871X4= 0.951 7.999X1 + 0.869X2 - 5.663X3 - 7.375X4= -0.812 3.725X1 + 8.007X2 - 2.916X3 - 6.664X4= -2.538 |
| Варіант 5 1.067X1 + 3.809X2 - 5.114X3 - 9.031X4= -7.272 -4.157X1 + 3.701X2 + 5.717X3 + 0.028X4= -3.803 -4.724X1 + 5.333X2 - 9.564X3 - 4.327X4= -5.141 8.394X1 - 1.890X2 - 3.166X3 - 9.602X4= -8.883 |
| Варіант 6 0.893X1 + 5.862X2 - 6.596X3 - 8.056X4= 3.547 -6.431X1 + 7.731X2 + 6.375X3 - 8.256X4= -5.859 0.134X1 + 3.569X2 + 6.317X3 - 8.725X4= 1.981 -6.815X1 + 6.510X2 - 7.946X3 - 1.150X4= -7.049 |
| Варіант 7 2.815X1 - 7.646X2 - 6.995X3 + 3.399X4= -5.249 -4.158X1 - 5.249X2 - 5.741X3 - 3.833X4= -5.139 -6.054X1 - 5.388X2 - 5.679X3 + 6.817X4= -5.111 -3.891X1 - 5.209X2 - 9.367X3 + 7.959X4= -9.982 |
| Варіант 8 9.984X1 - 6.794X2 - 5.896X3 + 9.862X4= -9.804 -3.220X1 - 8.652X2 + 6.060X3 - 2.786X4= -9.648 -8.168X1 + 1.292X2 + 4.412X3 - 4.068X4= -6.622 -1.509X1 + 1.498X2 - 8.996X3 - 0.677X4= 6.045 |
| Варіант 9 6.780X1 + 6.227X2 + 0.133X3 - 3.933X4= 6.629 -9.701X1 - 9.705X2 - 8.332X3 - 1.893X4= -6.501 -3.926X1 - 9.092X2 + 1.859X3 + 5.973X4= -5.174 -3.431X1 + 1.346X2 + 6.975X3 + 4.825X4= -4.748 |
| Варіант 10 0.917X1 - 3.243X2 + 7.527X3 + 9.556X4= -0.222 -6.892X1 - 8.607X2 - 2.539X3 + 4.458X4= -0.035 -4.596X1 - 9.738X2 - 3.964X3 + 4.529X4= 6.881 -9.856X1 - 6.934X2 - 9.846X3 - 8.484X4= 3.696 |
| Варіант 11 -5.253X1 - 9.071X2 - 3.960X3 + 1.717X4= -3.470 3.019X1 - 2.433X2 + 9.716X3 + 0.880X4= 2.486 3.738X1 + 2.640X2 - 6.742X3 - 8.617X4= -7.706 -6.519X1 - 8.621X2 - 1.401X3 + 6.562X4= -8.523 |
| Варіант 12 -3.849X1 - 6.298X2 + 0.456X3 - 5.146X4= -4.117 -8.976X1 + 6.111X2 - 8.514X3 - 3.188X4= -8.191 -8.605X1 - 0.822X2 - 7.741X3 - 6.778X4= -6.269 6.888X1 + 1.331X2 - 0.773X3 + 8.717X4= -4.840 |
| Варіант 13 -1.482X1 + 6.658X2 + 7.998X3 + 4.923X4= -9.898 6.737X1 - 2.874X2 - 6.432X3 - 5.811X4= -2.626 -6.219X1 - 2.772X2 - 2.434X3 - 6.877X4= 5.550 4.642X1 + 6.562X2 - 2.724X3 - 6.679X4= -1.342 |
| Варіант 14 -1.281X1 - 1.954X2 - 0.488X3 - 0.208X4= -1.808 0.903X1 + 2.833X2 + 4.167X3 - 4.456X4= 4.576 -7.571X1 - 7.427X2 + 8.728X3 + 8.896X4= -2.714 9.281X1 - 2.525X2 - 1.071X3 - 9.702X4= 6.040 |
| Варіант 15 -0.492X1 + 8.095X2 - 5.811X3 - 1.096X4= 5.478 3.365X1 - 9.676X2 + 3.101X3 + 3.128X4= -1.427 -9.944X1 + 2.277X2 + 9.601X3 - 0.851X4= 7.054 4.851X1 + 2.404X2 - 5.224X3 - 8.136X4= 5.614 |
| Варіант 16 4.359X1 - 2.271X2 + 5.041X3 - 8.600X4= -0.695 1.102X1 + 5.492X2 - 5.900X3 + 9.261X4= 7.585 -7.360X1 - 4.594X2 - 3.866X3 - 7.838X4= -6.070 -1.806X1 - 0.743X2 + 9.852X3 - 5.126X4= -7.894 |
| Варіант 17 -8.141X1 - 3.238X2 + 9.762X3 - 7.753X4= -9.037 7.099X1 - 3.721X2 + 0.251X3 - 6.981X4= -6.020 9.160X1 + 5.789X2 - 5.053X3 - 4.199X4= 9.671 1.982X1 + 7.959X2 - 7.683X3 + 6.439X4= -7.467 |
| Варіант 18 -7.245X1 - 4.746X2 - 7.518X3 + 3.840X4= -9.634 4.383X1 + 0.230X2 - 5.712X3 + 8.494X4= 2.931 6.697X1 - 8.895X2 - 8.425X3 - 8.813X4= -2.491 -6.706X1 + 2.978X2 - 5.414X3 - 8.411X4= -4.405 |
| Варіант 19 -5.490X1 + 2.072X2 - 5.387X3 - 1.754X4= -3.051 -3.202X1 + 2.506X2 + 3.695X3 + 3.596X4= 5.541 -8.164X1 - 9.165X2 - 6.115X3 + 3.521X4= -4.344 -8.026X1 - 3.997X2 - 2.761X3 - 4.021X4= -6.125 |
| Варіант 20 -1.494X1 - 1.694X2 - 1.682X3 - 8.476X4= -3.308 -1.306X1 + 6.988X2 - 0.571X3 + 7.312X4= -3.014 1.543X1 - 7.812X2 - 0.382X3 - 4.658X4= -8.800 3.068X1 - 7.369X2 - 4.622X3 - 7.091X4= -2.363 |
| Варіант 21 3.182X1 - 4.081X2 - 5.773X3 + 8.682X4= -8.010 -7.375X1 - 4.511X2 - 3.902X3 - 5.656X4= -0.500 -5.677X1 - 8.855X2 + 5.007X3 - 7.731X4= 9.878 1.512X1 + 4.616X2 - 6.371X3 - 4.611X4= -3.285 |
| Варіант 22 0.428X1 + 9.616X2 + 6.036X3 - 3.468X4= 6.609 -7.557X1 - 3.882X2 - 1.792X3 - 9.518X4= -6.300 9.471X1 - 9.109X2 + 4.793X3 - 5.208X4= 6.874 -6.201X1 + 7.569X2 - 2.278X3 - 7.187X4= -0.714 |
| Варіант 23 -5.813X1 + 7.630X2 + 5.929X3 - 2.214X4= -6.796 -5.136X1 - 3.579X2 + 5.374X3 - 6.675X4= 2.161 9.217X1 - 1.282X2 + 3.215X3 + 7.435X4= 7.311 -6.873X1 + 1.622X2 - 7.050X3 - 7.614X4= -2.487 |
| Варіант 24 -3.514X1 - 8.579X2 - 8.191X3 - 7.556X4= -9.006 -3.326X1 - 1.575X2 - 4.410X3 - 1.930X4= -6.694 -4.042X1 - 0.211X2 - 8.169X3 - 6.680X4= -8.012 -7.011X1 - 7.126X2 + 0.500X3 - 7.579X4= 9.937 |
| Варіант 25 6.311X1 - 9.332X2 + 7.164X3 - 3.499X4= 9.060 -1.190X1 - 3.289X2 - 6.024X3 - 5.371X4= -1.914 -9.479X1 - 2.213X2 - 5.868X3 + 4.301X4= -4.296 3.827X1 - 8.897X2 - 5.339X3 - 2.483X4= 8.494 |
| Варіант 26 0.733X1 - 1.591X2 - 9.246X3 + 6.641X4= 8.925 -2.679X1 - 7.656X2 - 6.556X3 - 8.759X4= -2.914 9.175X1 + 7.572X2 - 2.851X3 - 1.038X4= -7.309 -1.370X1 - 3.854X2 - 8.096X3 + 4.387X4= 1.420 |
| Варіант 27 0.308X1 + 3.431X2 - 1.460X3 + 0.531X4= -5.597 -8.806X1 - 1.331X2 - 6.545X3 - 0.041X4= 0.652 -4.705X1 + 6.137X2 - 6.115X3 + 0.436X4= 9.469 -6.751X1 - 6.781X2 - 3.157X3 - 3.094X4= 6.662 |
| Варіант 28 -6.960X1 - 3.971X2 + 8.160X3 + 3.154X4= -8.119 -2.934X1 + 1.010X2 - 8.832X3 + 5.985X4= 7.871 -3.528X1 - 6.058X2 + 1.384X3 - 5.378X4= 8.039 -9.502X1 - 4.212X2 + 9.937X3 + 5.340X4= 6.834 |
| Варіант 29 0.516X1 + 1.168X2 + 5.848X3 - 7.526X4= 2.715 -9.195X1 - 3.881X2 - 9.791X3 - 2.940X4= -8.143 -5.059X1 - 5.637X2 + 9.493X3 + 7.762X4= -6.830 4.054X1 + 6.444X2 - 3.172X3 - 2.123X4= -2.320 |
| Варіант 30 6.340X1 + 2.731X2 - 6.129X3 + 5.436X4= -6.051 -4.035X1 + 6.198X2 + 3.685X3 - 5.727X4= -8.036 -4.869X1 - 8.315X2 - 0.896X3 + 1.293X4= 6.021 5.346X1 + 7.673X2 + 6.335X3 + 4.153X4= -7.508 |
Задача 2. Відомі координати векторів 
(за варіантами 1-30) в деякому ортонормованому базисі. Необхідно:
1. обчислити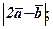 
2. знайти координати одиничних векторів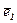 
і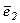 
, колінеарних
вектору 
3. обчислити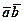 
, 
, 
;
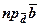4. обчислити роботу А сили 
при переміщені матеріальної
точки з точки D(5,9,-8) у точку E(4,7,-6);
5. знайти координати одного з векторів 
, ортогональних
кожному з векторів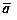 
і 
6. обчислити модуль векторного добутку 
7. знайти момент 
сили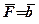 
відносно точки P(-2,3,5), якщо
сила прикладена до важеля PQ у точці Q(-1,2,8);
8. обчислити мішаний добуток векторів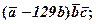 
9. обчислити площу S трикутника, побудованого на
векторах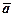 
і
10. обчислити 
, де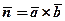 
та з’ясувати, який
геометричний зміст має величина Н;
11. обчислити об’єм V піраміди, побудованої на векторах
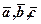(для контролю використати формулу 
);
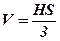12. Підібрати такі значення числового параметру t, щоб вектори
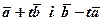, були ортогональні;
13. упевнитися, що система векторів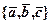 
утворює базис, та
знайти координати вектора 
у цьому базисі.
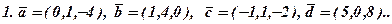
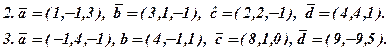
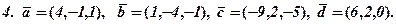
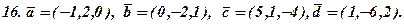
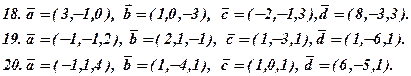
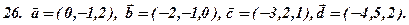
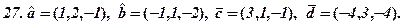
Задача 3. Відомі координати вершин трикутника ABC (за варіантами 1-30). Необхідно:
1. знайти координати нормального вектора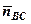 
і кутовий коєфіцієнт 
прямої ВС;
2. з’ясувати, чи є трикутник АВС прямокутним;
3. скласти рівняння прямої АА1, паралельної до прямої ВС;
4. скласти рівняння висоти АН;
5. скласти рівняння медіани ВМ;
6. обчислити координати точки перетину Е прямих АН і ВМ;
7. обчислити довжину h висоти АН двома способами: як відстань від точки А до прямої ВС і як модуль проекції вектора СА на вектор ;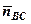
8. обчислити площу S трикутника АВС трьома способами за формулами: 
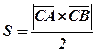(з цією метою перейти у тривимірний простір, поклавши треті координати векторів 
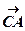і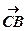 
равнимі 0); 
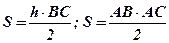(остання формула застосовується тільки при умові 
);
9. обчислити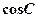 
і 
(для контролю використати тотожність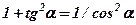 
);
10. скласти рівняння бісектриси AF внутрішнього кута А трикутника АВС (пропонуємо використати рівність відстаней від довільної точки N(х,у) бісектриси до сторін кута; для контролю обчислити кути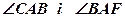 
);
11.накреслити трикутник АВС за координатами його вершин, побудувати прямі АА1, АН, ВМ і AF за їх рівняннями та перевірити відповідність координат точки Е малюнку.
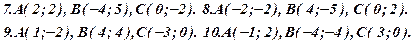
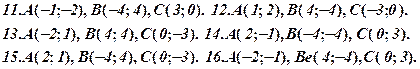
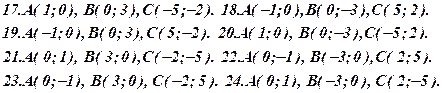
Задача 4. Відомі координати точок А, В, С, D (за варіантами 1-30). Необхідно:
1. побудувати піраміду АВСD за координатами її вершин;
2. скласти рівняння площини АВС;
3. обчислити кут між площинами АВС і хОу;
4. обчислити кут між площиною АВС і віссю Оz;
5. вказати взаємне розміщення осі Оу і площини АВС (тобто з’ясувати, чи паралельні Оу і АВС, чи Оу належить до АВС, чи Оу і АВС перетинаються в єдиній точці);
6. скласти рівняння площини (Р), що проходить через точки В і С перпендикулярно до площини хОу;
7. скласти канонічне рівняння перпендикуляра АF до площини (Р) (точка F - основа перпендикуляра);
8. обчислити координати точки F;
9. обчислити довжину АF трьома способами: як відстань між точками А і F, як модуль проєкції вектора 
на нормальний вектор 
площини (Р), а також як відстань А до площини (Р);
10. скласти рівняння площини (Q), що проходить через пряму АD паралельно до прямої ВС;
11. обчислити відстань між прямими ВС і АD;
12. скласти рівняння прямої ВС та обчислити координати точки перетину Е прямої ВС з площиною хОу;
13. скласти параметричні рівняння проекції прямої ВС на площину хОу;
14. обчислити відстань від осі Оz до прямої ВС;
15. обчислити відстань від осі Оz до площини ВОС.
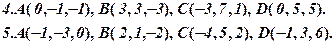
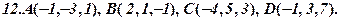
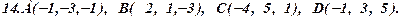
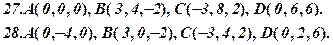
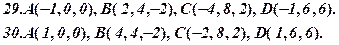
Задача 5. Дано рівняння деяких ліній. Необхідно:
- визначити типи лінії;
- побудувати лінії за їх рівнянням.
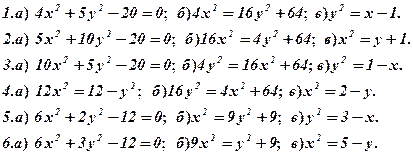
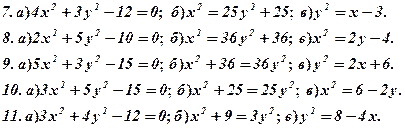
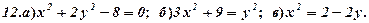
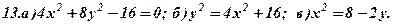
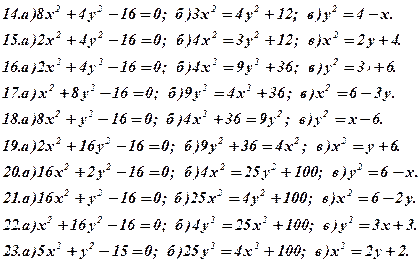
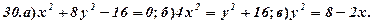
Задача 6. Визнаити типи поверхонь, поданих вказаними рівняннями (варіант 1-30). Схематично зобразити ці поверхні та їх перерізи координатними площинами.
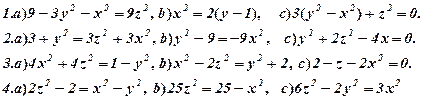
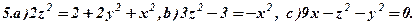
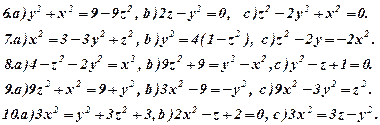
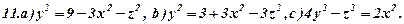
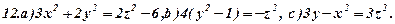
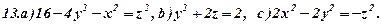
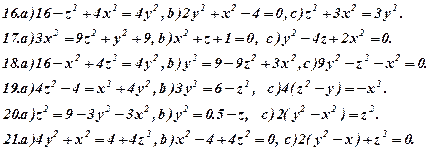
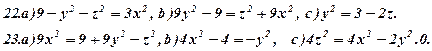
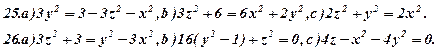
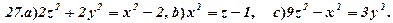
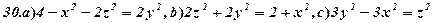
Задача 7. Зобразити кожне з тіл, обмежених даними поверхнями.
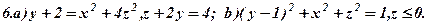
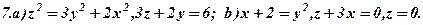
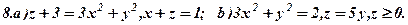
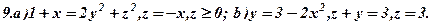
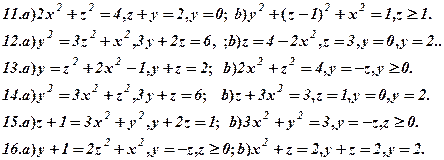
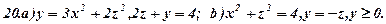
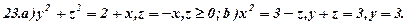
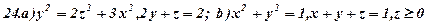
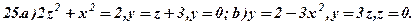
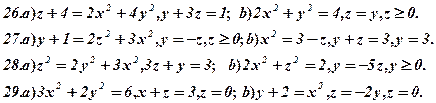
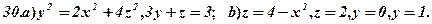
Задача 8. За варіантами 1 - 30 дано полярне рівняння лінії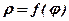 
(
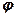-полярний кут, 
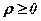- полярний радіус). Необхідно:
а) побудувати за точками задану лінію;
б) використовуючи зв’язок між полярними та прямокутними координатами, рівняння 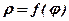перетворити в рівняння 
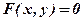у прямокутних координатах.
Вказівка. Скласти таблицю значень 
і :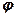
|
| 
| 
| 
| … |
| 
| 
| 
| … |
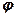
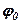
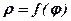
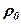
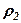
Куту 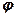надавати значень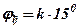 
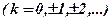або інших. Додатково обчислити 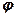, для якого = 0. Потім обрати полюс, полярну вісь, масштаб, побудувати точки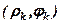 
(при умові 
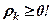) і сполучити ці точки плавною лінією. Для перевірки обчислень, рівняння 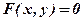шляхом виділення повних квадратів звести до вигляду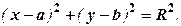 
| 1. |  .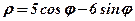
| 2. |  .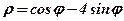
|
| 3. |  .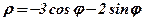
| 4. |  .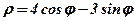
|
| 5. |  .
| 6. |  .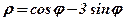
|
| 7. |  .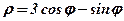
| 8. |  .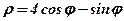
|
| 9. |  .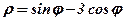
| 10. |  .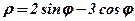
|
| 11. |  .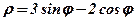
| 12. |  .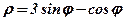
|
| 13. |  .
| 14. |  .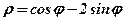
|
| 15. |  .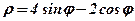
| 16. |  .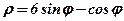
|
| 17. |  .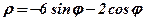
| 18. |  .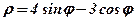
|
| 19. |  .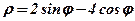
| 20. |  .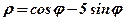
|
| 21. |  .
| 22. |  .
|
| 23. |  .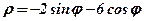
| 24. |  .
|
| 25. |  .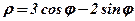
| 26. |  .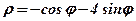
|
| 27. |  .
| 28. |  .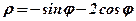
|
| 29. |  .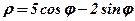
| 30. |  .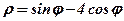
|
Задача 9. Побудувати за точками лінію, задану полярним рівнянням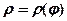 
(Для контролю визначити інтервали монотонності та симетрію значень 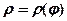відносно .)
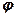| 1. |  .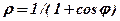
| 2. |  .
|
| 3. |  .
| 4. |  .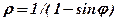
|
| 5. |  .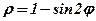
| 6. |  .
|
| 7. |  .
| 8. |  .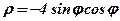
|
| 9. |  .
| 10. |  .
|
| 11. |  .
| 12. |  .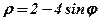
|
| 13. |  .
| 14. |  .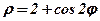
|
| 15. |  .
| 16. |  .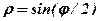
|
| 17. | .
| 18. |  .
|
| 19. |  .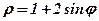
| 20. |  .
|
| 21. |  .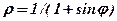
| 22. |  .
|
| 23. |  .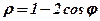
| 24. |  .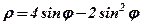
|
| 25. |  .
| 26. |  .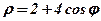
|
| 27. |  .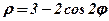
| 28. |  .
|
| 29. |  .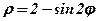
| 30. |  .
|
Задача 10. Дано комплексні числа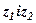 
. Обчислити вираз 
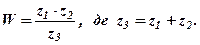Для контролю перевірити рівність 
.
| 
|
|
| ||
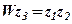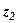
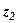
| 1. | 
| 
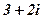
| 2. |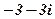 
| 
|
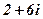
| 3. |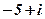 
| 
| 4. | 
| 
|
| 5. |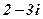 
| 
| 6. |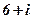 
| 
|
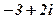
| 7. | 
| 
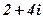
| 8. |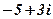 
| 
|
| 9. |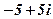 
|
| 10. |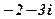 
| 
|
| 11. |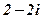 
|
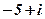
| 12. | 
| 
|
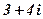
| 13. |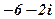 
| 
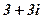
| 14. | 
|
|
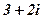
| 15. |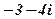 
| 
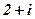
| 16. |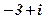 
| 
|
| 17. |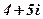 
| 
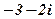
| 18. | 
| 
|
| 19. |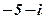 
| 
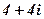
| 20. |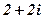 
| 
|
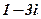
| 21. |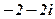 
| 
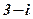
| 22. |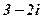 
|
|
| 23. |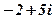 
|
| 24. |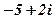 
| 
|
| 25. |
| 
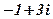
| 26. | 
|
|
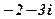
| 27. |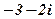
| 
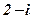
| 28. |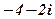 
| 
|
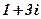
| 29. |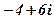 
| 
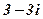
| 30. |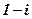 
|
|
Задача 11. Знайти корені поданого квадратного тричлена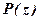 
на множині комплексних чисел; розкласти 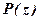в добуток лінійних множників. Перевірку виконати безпосередньою підстановкою коренів в 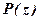та перетворенням добутку лінійних множників до .
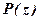| 1. | 
| 2. |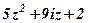 
| 3. | 
|
| 4. | 
| 5. |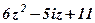 
| 6. |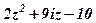 
|
| 7. |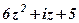 
| 8. | 
| 9. |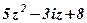 
|
| 10. | 
| 11. |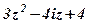 
| 12. |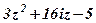 
|
| 13. |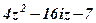 
| 14. | 
| 15. | 
|
| 16. |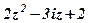 
| 17. |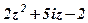 
| 18. | 
|
| 19. |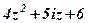 
| 20. | 
| 21. | 
|
| 22. | 
| 23. |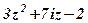 
| 24. |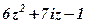 
|
| 25. |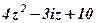 
| 26. | 
| 27. |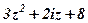 
|
| 28. | 
| 29. |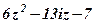 
| 30. | 
|
Задача 12. Знайти корені поданого квадратного тричлена на множині комплексних чисел. Перевірку коренів виконати за допомогою формул Вієта. Для перевірки скористатися формулами Вієта.
| 1. |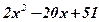 
| 2. |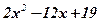 
| 3. |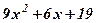 
|
| 4. | 
| 5. | 
| 6. |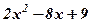 
|
| 7. |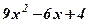 
| 8. |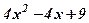 
| 9. |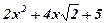 
|
| 10. | 
| 11. |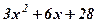 
| 12. |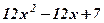 
|
| 13. |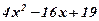 
| 14. |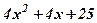 
| 15. |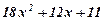 
|
| 16. | 
| 17. |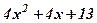 
| 18. |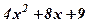 
|
| 19. |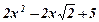 
| 20. |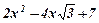 
| 21. | 
|
| 22. | 
| 23. |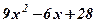 
| 24. | 
|
| 25. |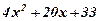 
| 26. | 
| 27. | 
|
| 28. |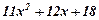 
| 29. | 
| 30. | 
|
Задача 13. Дано комплексні числа 
, 
. Необхідно:
а) використовуючи алгебраичну форму чисел , , обчислити вираз 
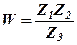, де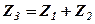 
;
б) обчислити 
іншим способом, виконуючи дії з числами , , 
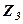в показниковій формі (для контролю відповідь за допомогою формули Ейлера записати в алгебраичному вигляді і порівнняти з результатом пункту а).
|
|
|
|
| ||
| 1. | 4-7i | -3+4i | 2. | 1-i | -7+4i |
| 3. | -5+4i | 7-4i | 4. | -6-2i | 4+I |
| 5. | 3-2i | 8+2i | 6. | 2-8i | 3+8i |
| 7. | 1+2i | 6+I | 8. | -5-4i | -1+2i |
| 9. | -6-i | -4-5i | 10. | 6+4i | -2+2i |
| 11. | 5-3i | -5-7i | 12. | -3-i | 2-4i |
| 13. | -7+i | -4-3i | 14. | -2+4i | -6-3i |
| 15. | -5-3i | -2-i | 16. | -3+5i | 4-8i |
| 17. | 9+2i | 3-7i | 18. | -5+2i | 1+3i |
| 19. | 7+4i | 4+3i | 20. | -4-5i | 3+3i |
| 21. | -6-i | 4-2i | 22. | -4-2i | 5+4i |
| 23. | -3-6i | 4+3i | 24. | -4+3i | 6-7i |
| 25. | -2-3i | -1+5i | 26. | -5+3i | 1-2i |
| 27. | -4+6i | 3-3i | 28. | 4-5i | 2+4i |
| 29. | -5-i | 4+4i | 30. | -2+5i | -4-3i |
