1. Нехай ненульові вектори 
колінеарні, 
, тобто існує таке число 
, що 
. В координатній формі:
(1)
Отже, умовою колінеарності двох векторів є пропорційність їх відповідних координат.
Приклад. Чи колінеарні вектори
?
Розв’язання. За умовою 
=(1,2,-3),
=(-3,-6,9), а за
формулою (1) маємо 
, або ще можна записати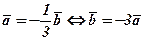 
.
2. Поділ відрізка в даному відношенні. Знайти координати точки М(х,у,z), яка ділить відрізок 
в заданому відношенні 
(рис. 14), якщо відомі координати точки 
і 
, тобто:
М
 |
Рис.14
Розглянемо вектори 
і 
. Оскільки 
і 
, то згідно з умовою (1) колінеарності векторів маємо
Зокрема, якщо точка М ділить відрізок пополам, то 
і координати середини відрізка:
Задача. Знайти координати центра мас трикутника АВС, у вершинах А(4,0,-2), В(-2,6,4), С(7,-3,4) якого зосереджені одиничні точкові маси.
Розв’язання. Побудуємо вершини трикутника за їх координатами (див. рис.) А(4,0,-2), В(-2,6,4), С(7,-3,4).
Знайдемо середину відрізка АВ, це точка М – основа медіани:
, 
M(1,3,1).
Відомо, що центр трикутника має знаходитись на перетині медіан, а медіани, перетинаючись, діляться у відношенні 2:1, починаючи від вершини, тобто
,
, 
.
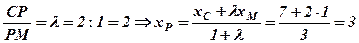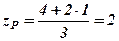Отже, Р(3,1,2)- центр мас трикутника АВС.
