Виконання вправ. Множини можуть складатися з будь-яких об'єктів різної при­роди

5 Дано: Μ == { a, b, с, d }, N = { b, d}. Знайдіть:

M\N; б) N\M; в) (Μ \ Ν) U (Ν \ Μ).

Множини можуть складатися з будь-яких об'єктів різної при­роди. Для математики особливо важливу роль відіграють мно­жини складені із «математичних об'єктів» — чисел, геометрич­них фігур тощо. Дуже часто зустрічаються числові множини, тобто множини, елементами яких є числа. Згадаємо деякі мно­жини чисел, з якими ви знайомилися в курсі математики.

1 Множина натуральних чисел тобто чисел, які виникають в процесі лічби предметів. Цю множину чисел позначають бук­вою N:

N = {1, 2, 3, 4, 5, 6,...}.

В цій множині завжди можна виконати дії додавання і мно­ження (віднімання і ділення не завжди можна виконати в мно­жині натуральних чисел тобто результат віднімання і ділення двох натуральних чисел не завжди є натуральним числом).

2 Об'єднання натуральних чисел, чисел протилежних до нату­ральних і числа 0 утворює множину цілих чисел, яку позна­чають буквою Z:

Z = {0, ±1, ±2, ±3,...}.

В цій множині завжди можна виконати дії додавання, віднімання та множення. Проте частка двох цілих чисел не завж­ди є числом цілим.

3 Множина раціональних чисел (її позначають буквою Q) — це множина чисел, які можна подати у вигляді нескоротного дробу , де т є Ζ, n є N

Q = { х: х = , m Ζ, n Ν}.

Кожне раціональне число можна подати у вигляді нескінчен­ного періодичного дробу. Наприклад = 0,333... = 0,(3). В множині раціональних чисел завжди виконуються дії додавання, віднімання, множення, ділення (крім ділення на 0). Проте, квад­ратний корінь з раціонального числа не завжди є раціональним числом. Наприклад: , і т. д.

4 Числа, які не можна подати у вигляді дробу , де т Z, n Ν (або числа, які подаються у вигляді нескінченного не­періодичного дробу, наприклад π = 3,1415926...), утворюють множину ірраціональних чисел.

Об'єднання раціональних і ірраціональних чисел утворює множину дійсних чисел, яку позначають буквою R.

У множині дійсних чисел завжди можна виконати дії: дода­вання, віднімання, множення, ділення (крім ділення на 0), до­бування квадратного кореня з невід'ємного числа.

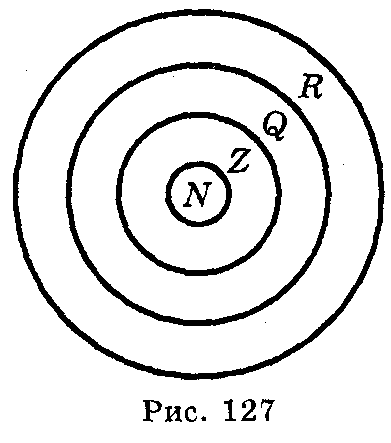
На рисунку в вигляді діаграми Ейлера подано співвідношення між числовими множинами:

N Ζ ; Q R