Пример разложения несинусоидального колебания на составляющие Пример разложения показан на рис. 74. Заметим, что исходная, несинусоидальная кривая имеет "провал" в середине каждого полупериода, а также два "горба". Вся кривая смещена по вертикали относительно горизонтальной оси графика.
Для упрощения здесь специально подобраноколебание, форма которого мало отличается от синусоиды. Поэтому в разложении данной кривой в ряд Фурье будет небольшое число составляющих.
В этом простейшем примере разложения несинусоидального колебания в ряд Фурье содержится только три составляющих: первая гармоника –u1,третьягармоника – u3, а также постоянная составляющая –U0.
Рассмотрим теперь, каким образом сумма составляющих даёт исходноенесинусоидальное колебание.
Рассмотрев первый полупериод несинусоидального колебания, можно понять, что "провал" образуется при сложении положительной амплитуды первой гармоники и отрицательной амплитуды третьей гармоники.
“Горбы” образуются от сложения положительных полупериодов первой и третьей гармоник.
Постоянная составляющая сдвигает несинусоидальное колебание выше горизонтальной оси. Она появляется в разложении том случае, если исходное колебание несимметрично относительно горизонтальной оси. Если сложить только гармоники, несинусоидальное напряжение будет симметричным относительно оси времени на графике.
Математическая запись разложения в ряд Фурьевыглядит как сумма всех составляющих: постоянной составляющей и гармоник. Для нашего примера несинусоидальное колебание запишется как сумма всех его составляющих:
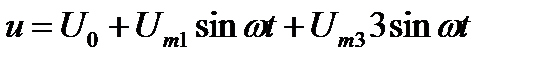
Из записи видно, что частота третьей гармоники втрое выше частоты первой гармоники.
Следует понимать, что каждая составляющая несинусоидального напряжения, приложенного к цепи, стремится вызвать в цепи соответствующую составляющую тока. Другими словами, постоянная составляющая напряжения стремится вызвать в цепи постоянную составляющую тока, первая гармоник напряжения породит первую гармонику тока и т.д. В целом, несинусоидальное напряжение, приложенное к цепи вызовет появление несинусоидального тока в цепи.
Таким образом, математическая запись тока, возникшего в цепи, для нашего примера, может выглядеть так:
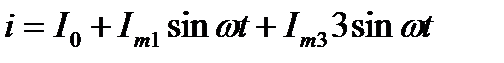
Заметим, что форма колебания для тока в цепи не обязательно будет совпадать с формой напряжения, приложенного к цепи. Это зависит от вида электрической цепи и присутствующих в ней компонентов.
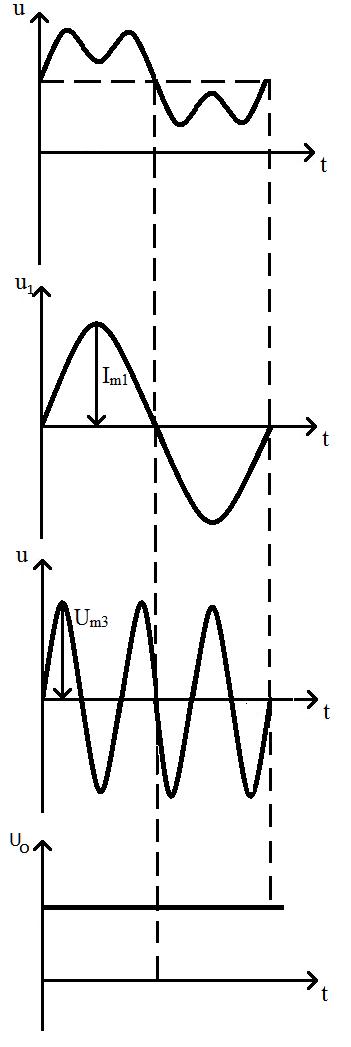
Рис. 74. Разложение несинусоидального колебания в ряд Фурье: а) u – исходное несинусоидальное колебание; б) u1– первая гармоника,
в) u3– третья гармоника;
г) Uo – постоянная составляющая.






