Провод, свёрнутый в форме спирали, называется катушкой (обмоткой). Катушка индуктивности по устройству напоминает обычную катушку ниток. Только в катушке индуктивности на сердечник (каркас) наматывают не нитки, а много витков изолированного провода.
Главным параметром катушки индуктивности является её индуктивность L. Повторите понятие "индуктивность", в разделе "Явление самоиндукции".
Термин “индуктивность”в электротехнике может означать:
1) параметр проводника (катушки), характеризующий его свойства в отношении величины наводимой в нём ЭДС самоиндукции;
2) собственно катушку, обладающую некоторой индуктивностью.
На рис. 51 показано условное графическое обозначение катушки индуктивности. К катушке приложено синусоидальное (переменное) напряжение U.
Рис. 51. Условное обозначение катушки индуктивности L. К катушке приложено переменное напряжение.
Катушкой индуктивности в электротехнике часто называют обмотку трансформатора или электродвигателя.
Через катушку индуктивности, показанную на рис. 51, проходит переменный ток I. Он создает вокруг катушки переменное магнитное поле. Это поле наводит в катушке ЭДС самоиндукцииeL. Величина ЭДС самоиндукции, наводимой в катушке, зависит от индуктивности катушки Lи скорости изменения токав цепи 
I/ 
t.
В соответствии с правилом Ленца, ЭДС самоиндукции препятствует протеканию тока в цепи. Препятствие протеканию тока означает, что катушка индуктивности обладает сопротивлением, которое называется индуктивным.
Индуктивное сопротивление XL можно вычислить по формуле:
(Ом), где:
f - частота приложенного напряжения;
L - индуктивность катушки (Генри).
Из формулы следует, что индуктивное сопротивление зависит от частоты f приложенного напряжения. С увеличением частоты индуктивное сопротивление катушки увеличивается.
Ток в цепи катушки индуктивности можно определить по закону Ома:
При повышении частоты приложенного напряжения Uиндуктивное сопротивление растёт, а ток в цепи уменьшается.
Катушка индуктивности относится к классу реактивных элементов. К реактивным относятся элементы, в которых происходит обратимое преобразование энергии. В катушке периодически повторяются процессы накопления энергии в магнитном поле катушки и возвращении накопленной энергии генератору.
Мощность, выделяющаяся в катушке, называется реактивной и определяется по формуле:
,
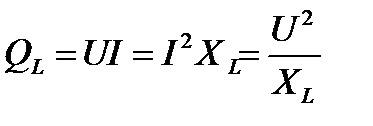
где "вар" – вольт-ампер реактивный.
Ток в катушке не совпадает по фазе с напряжением, приложенным к ней. Ток отстает от напряжения по фазе на угол π/2 рад (90 градусов).
Рис. 52. Ток в катушке индуктивности отстаёт по фазе от напряжения
Пример 11. Идеальная индуктивность в цепи синусоидального тока
В сеть с действующим значением напряжения 120В частотой f = 50 Гц включена катушка с индуктивностью L= 127 мГн. Определить ток, протекающий через катушку и выделяющуюся в ней реактивную мощность.
Решение.
Идеальная катушка индуктивности обладает только одним параметром – индуктивностью L. Активное сопротивление провода, которым она намотана, не учитывается.
Индуктивность катушки приведена в условии задачи в миллигенри (мГн). В расчётных формулах следует все величины выражать в основной размерности. Поэтому, переведём индуктивность из миллигенри в генри. Приставка "милли" означает одну тысячную долю
127 мГн = 127/1000 Гн = 0,127 Гн.
Индуктивное сопротивление катушки:
ХL=2pfL= 2p · 50 · 0,127 = 40 Ом.
Ток в катушке, по закону Ома:
I= U/XL = 120 /40 = 3 А.
В катушке выделяется реактивная мощность
Q=U · I =120 · 3 = 360 вар.
29. Свойства ёмкости в цепи синусоидального тока. Волновая и векторная диаграммы. Зависимость сопротивления конденсатора от частоты. Понятие реактивного сопротивления.
Конденсатор представляет собой две металлические пластины (обкладки), разделённые диэлектриком. Если приложить к конденсатору постоянное напряжение, на его обкладки поступит электрический заряд, как показано на рис. 53. Полученный заряд может сохраняться на обкладках долгое время. Заряды со знаком "плюс" и "минус" притягиваются друг к другу и не могут уйти с обкладок. В то же время они не могут и соединиться, нейтрализовав друг друга, т.к. этому препятствует диэлектрик (изоляция) между обкладками. Таким образом, конденсатор это устройство, предназначенное для накопления и хранения электрического заряда. (Поскольку изоляция между обкладками неидеальна, рано или поздно конденсатор разрядится – потеряет заряд)
Рис. 53. Конденсатор хранит заряд на своих обкладках
Постоянный ток не может проходить через конденсатор. Этому препятствует диэлектрик между обкладками.
Рис. 54. В цепи переменного напряжения через конденсатор протекает ток.
Как ни странно, переменный ток может проходить в цепи с конденсатором, несмотря на наличие изоляции между обкладками.
При переменном напряжении конденсатор, при смене полупериода, вынужден постоянно перезаряжаться. При этом меняется полярность и величина заряда на обкладках конденсатора (см. рис. 54).
В положительный полупериод синусоиды на верхнюю обкладку конденсатора поступает положительный заряд, а на нижнюю – отрицательный.
В отрицательный полупериод (его полярность показана в скобках) заряд на обкладках меняется на противоположный.
При работе в цепях синусоидального тока конденсатор постоянно перезаряжается. В проводниках, подводящих напряжение к конденсатору, происходит перемещение заряда. Это означает, что в цепи протекает ток.
Вместо термина "конденсатор" часто используется термин "емкость". Это слово имеет в электротехнике два значения:
- параметр конденсатора, характеризующий его величину заряда, который он способен накапливать;
- собственно конденсатор.
Конденсатор оказывает сопротивление проходящему току. Это сопротивление называется ёмкостным, обозначается XCи определяется по формуле:
, где:
f - частота приложенного напряжения;
С - ёмкость конденсатора (Фарад).
Ёмкостное сопротивление зависит от частоты. С ее увеличением емкостное сопротивление уменьшается. Соответственно, ток в цепи с конденсатором увеличивается:
В конденсаторе ток опережает напряжение на угол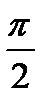 
радиан (90 градусов).
Рис. 55. В конденсаторе ток опережает по фазе приложенное напряжение
Конденсатор, как и катушка индуктивности, относится к реактивным элементам. В реактивных элементах происходит обратимое преобразование энергии. Конденсатор сначала забирает энергию от источника напряжения, накапливает энергию в своём электрическом поле, а затем отдает ее генератору. Затем процесс повторяется.
В конденсаторе выделяется реактивная мощность:
,
Пример 12. Идеальный конденсатор в цепи синусоидального тока.
К конденсатору емкостью С = 63,7 мкФ приложено напряжение u=141sin314t, В. Определить действующее значение тока и реактивную мощность конденсатора.
Решение.
Идеальный конденсатор обладает только одним параметром – ёмкостью. Влияние сопротивления изоляции между обкладками не учитывается.
В условии задачи приведено уравнение напряжения, действующего на входе цепи, имеющее вид: u = Umsinwt. Из этого уравнения можно узнать амплитуду приложенного напряжения Um =141В и угловую частоту w = 314рад/сек.
Зная амплитуду Um, приложенного напряжения, находим действующее значение напряжения U=Um/1,41=141/1,41=100B.
Зная, что угловая частота w = 2pf, находим частоту приложенного к конденсатору напряжения f = w/2p =314/6,28=50Гц.
Емкостное сопротивление конденсатора
Xc=1/2pfC=1 / 6,28·50·63,7·10-6=50 Ом.
В этой формуле ёмкость конденсатора выражена в фарадах, для чего, предварительно, был сделан перевод ёмкости конденсатора из микрофарад, приведённых в условии задачи, в фарады. Приставка "микро" обозначает одну миллионную долю, следовательно:
63,7мкФ = 63,7/1000000 Ф = 63,7·10-6 Ф.
Ток в цепи, по закону Ома
I = U /Xс = 100/50 = 2 А.
Реактивная мощность
Qc = UI = 100 • 2 = 200 вар.
30. Проведите сравнение свойств конденсатора и индуктивности в цепи переменного тока. Поясните, в чём эти элементы схожи и в чём различны. Приведите необходимые формулы и векторные диаграммы.
31. Понятие об идеальных и реальных компонентах электрической цепи. Последовательное соединение элементов RL и элементов RC. Векторные диаграммы, расчётные формулы, свойства.
Последовательное соединение резистора и индуктивности
(цепочка RL)
Ранее была рассмотрена идеальная катушка индуктивности, где мы учитывали только один параметр – индуктивность катушки. Для реальной катушки индуктивности приходится учитывать не только её индуктивность L, но и сопротивление R–провода, которыми она намотана. К реальным катушкам индуктивности относятся, например, обмотки трансформаторов и электродвигателей.
На схеме реальная катушка индуктивности изображается последовательным соединением элементов R и L (рис. 57). На каждом из этих элементов действует напряжение, обозначенное на рис. 57 стрелкой. На сопротивлении действует активное напряжение Ua, а на индуктивности – индуктивное напряжение UL.
Рис. 57. Последовательное соединение элементов R иL
Известно, что при последовательном соединенииэлементов цепи общее напряжение равно сумме напряжений на этих элементах.
Сумма эта векторная, арифметически суммировать напряжения в цепях переменного тока нельзя. Складывать векторы можно только по рассмотренным выше правилам сложения векторов.
Для понимания работы электрической цепи переменного тока, прежде всего, необходимо построить векторную диаграмму. Для рассматриваемой цепи векторная диаграмма будет иметь вид, показанный на рис. 58.
В последовательных цепях построение диаграмм начинается с вектора тока, так как он одинаков во всех элементах цепи.
Рис. 58. Векторная диаграмма для цепи с последовательным соединением
элементов R и L
Затем проводим вектор напряжения на активном сопротивлении. Он совпадает по фазе с током в цепи.
К концу вектора Uaпристраиваем вектор напряжения ULна индуктивности. Он направлен вверх, поскольку напряжение на индуктивности опережает ток на 90 градусов.
Общее напряжение, приложенное к цепи является суммой этих двух векторов. Суммируя напряжения Uaи UL, проведём вектор суммарного напряжения Uоб из начала вектора Ua к концу вектора UL.
Из диаграммы следует, что ток в цепи отстаёт по фазе от приложенного к цепи напряжения Uоб на угол φ меньше 90 градусов.
Три напряжения на векторной диаграмме образуют треугольник напряжений. В этом прямоугольном треугольнике гипотенузой является напряжение Uоб,а катетами – напряжения Uaи UL.
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
(Здесь и далее, в формулах, стрелка 
заменяет слово "следовательно") По закону Ома, ток равен напряжению, делённому на сопротивление цепи:
,где
Z– полное сопротивление в цепи, которое учитывает совместное действие активного Rи индуктивногоXLсопротивлений.
Цепь содержит активный и реактивный компоненты. В резисторе выделяется активная мощность 
. В катушке выделяется реактивная мощность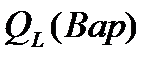 
. Во всей цепи выделяется полная мощность S, измеряемая в вольт-амперах (ВА).
(ВА)
Пример13. Реальная катушка в цепи синусоидального тока.
В сеть с напряжением 50 В и частотой 50 Гц включена реальная катушка с индуктивностью L = 0,0127 Гн. и активным сопротивлением R = 3 Ом. Определить ток, напряжения на элементах цепи, активную, реактивную и полную мощности катушки.
Решение
Реальная катушка индуктивности помимо индуктивности L обладает, также, сопротивлением провода R, которым она намотана. На схеме реальная катушка изображается последовательным соединением сопротивления R и индуктивности L.
Индуктивное сопротивление катушки
XL=2πfL = 2 · 3,14 · 50 · 0,0127 = 4Ом.
Полное сопротивление цепи
Ток определяется напряжением, приложенным к цепи, и её полным сопротивлением
I = Uоб /Z = 50/5 = 10 А.
Напряжения на активном и индуктивном сопротивлениях, входящих в цепь, определим по закону Ома:
напряжение на активном сопротивлении:Ua= I·R== 10 · 3 = 30 В;
напряжение на индуктивном сопротивлении:UL=I · XL = 10 · 4 = 40 В.
Активная, реактивная и полная мощности, выделяющиеся в элементах цепи:
Р = Uа · I = 30 · 10 = 300 Вт;
QL = UL · I= 40 · 10 = 400 вар:
S = Uоб·I = 50 · 10 = 500 BА.
