В электрической цепи, помимо активного сопротивления, могут быть включены одновременно два реактивных элемента: индуктивность Lи ёмкость С. Работа цепи в этом случае будет зависеть от того, какой из реактивных элементов преобладает.
Как известно, элементы Lи С обладают противоположными свойствами. В зависимости от того, какой из двух реактивных элементов преобладает, цепь будет вести себя как активно-индуктивная (действие индуктивности сильнее) или активно-ёмкостная (сильнее действие ёмкости). Действие более "слабого" реактивного элемента буден нейтрализовано действием более "сильного" элемента.

Рис. 61. Последовательное соединение элементов RLC
Чтобы понять процессы, происходящие в такой цепи, рассмотрим векторную диаграмму для случая преобладания индуктивности(рис. 62). Преобладание индуктивности возникает, если индуктивное сопротивление XL больше ёмкостногосопротивления XC.

Рис. 62. Векторная диаграмма для цепи с последовательным соединением
элементов RLC. Индуктивность в цепи преобладает
В последовательной цепи переменного тока, общее напряжение, приложенное к цепи, равно векторной сумме напряжений на элементах, входящих в цепь.
Прежде всего, проводится вектор тока I, одинаковый во всех элементахпоследовательной цепи. Затем, последовательно строятся векторы напряжений на элементах цепи: Uа,UL, иUC. При построении векторов напряжений учитываем их сдвиг по фазе относительно тока.
На диаграмма можно выделить прямоугольный треугольник напряжений, в котором гипотенузой является напряжение Uоб, а катетами являются напряжение Uа и разность напряжений (UL-UC).
По теореме Пифагора, для прямоугольного треугольника:

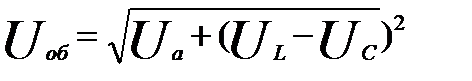
От треугольника напряжений можно перейти к треугольнику сопротивлений и к треугольнику мощностей. Если стороны треугольника напряжений, в масштабе, поделить на ток, то получится треугольник сопротивлений. Если же стороны треугольника напряжений умножить на ток, получим треугольник мощностей.
Используя теорему Пифагора, из треугольника сопротивлений и треугольника мощностей можно записать формулы для сопротивлений и мощностей:
полное сопротивление цепи  (Ом);
(Ом);
полная мощность 
 (ВА).
(ВА).
Все рассмотренные формулы записаны для случая, когда в цепи преобладает индуктивность. Однако, они будут справедливы и в случае, когда преобладает ёмкость. При этом, в скобке, входящей в формулу, будет получаться отрицательное значение. Этот факт не имеет значения и не влияет на результат вычисления.
Векторная диаграмма цепи, в которой преобладает ёмкость показана на рис. преобладает емкость, то диаграмма примет вид, показанный на рис. 63.Преобладание ёмкости возникает в случае, когда ёмкостноесопротивление XC больше индуктивного сопротивления XL.

Рис. 63. Векторная диаграмма для цепи с последовательным соединением
элементов RLC. В цепи преобладает ёмкость
Пример 15. Последовательное соединение элементов RLC в цепи синусоидального тока.
В цепи последовательно соединены элементы: активное сопротивление R = 12 Ом, индуктивное сопротивление ХL = 32 Ом и емкостное ХС = 16 Ом.Общее напряжение, приложенное к цепиUоб=120 В.
Определить ток в цепи, напряжение на каждом элементе, а также активную, реактивную и полную мощность.
Решение
Полное сопротивление цепи
 .
.
По закону Ома находим ток в цепи:

Напряжения на элементах цепи:
на резисторе
Uа= I*R;
на индуктивности
UL=I*XL;
наёмкости
UC=I*XC.
Мощности, выделяющиеся в цепи:
активная,выделяющаяся в сопротивлении,
Р = I2 · R=36 · 12 = 432 Вт;
реактивная, выделяющаяся в реактивных элементах,
Q= I2 · ( XL-XC) = 62 · 16 = 576 Вар;
полная, выделяющаяся в цепи в целом
S =UI = 120 · 6 = 720 ВА.
Резонанс напряжений. Определение. Условие получения. Векторная диаграмма для режима резонанса. Свойства цепи при резонансе. Влияние потерь в колебательном контуре. Резонансные кривые. Применение резонанса в технике.
Резонанс возникает в электрической цепи, содержащей реактивные элементы L и С. Как известно, эти элементы обладают противоположными свойствами. Ранее мы рассмотрели случаи, когда один из реактивных элементов преобладает над другим. Однако, самое интересное происходит, когда действие одного реактивного элемента полностью уравновешивает действие другого. При этом в цепи возникает режим электрического резонанса.
Резонансом называется режим, когда цепь содержит реактивные элементы, но ведет себя как активное сопротивление. При этом напряжение, приложенное к цепи, совпадает по фазе с током.
Физический смысл резонанса состоит в том, что индуктивность и ёмкость обмениваются между собой энергией. Процесс обмена энергией между индуктивностью и ёмкостью рассматривался вами при изучении курса физики (колебательный контур).
Различают резонанс двух видов: резонанс напряжений и резонанс токов.
Запомните главное: при резонансе свойства цепи резко изменяются в сравнении со случаем отсутствия резонанса.
Резонанс напряжений
Резонанс напряжений возникает в цепи с последовательным соединением реактивных элементов L и С. Вид схемы показан на рис. 64.

Рис. 64. Схема цепи, в которой может возникать резонанс напряжений
Резонанс возникает при выполнении условия возникновения резонанса:
 , или, в другой форме записи,
, или, в другой форме записи,


Таким образом, для возникновения резонанса требуется, чтобы реактивное сопротивление индуктивности было равно реактивному сопротивлению ёмкости.
Смысл этого условия можно понять, анализируя векторную диаграмму цепи, находящейся в режиме резонанса (рис. 65). Принцип построения векторной диаграммы для последовательной цепи рассмотрен ранее.

Рис. 65. Векторная диаграмма цепи, находящейся в режиме резонанса напряжений
Из диаграммы следует, что напряжения на реактивных элементах становятся равными, т.е. напряжение UL= I* XL равно напряжению UC=I*XС. При этом эти напряжения взаимно компенсируют друг друга. В результате, общее напряжение Uоб, приложенное к цепи совпадает по фазе с током, что и является проявлением резонанса.
В случае возникновения резонанса напряжений цепь приобретает очень интересные свойства:
1) угол φ сдвига по фазе между приложенным к цепи напряжением и протекающим в цепи током становится равен нулю градусов, соответственно, косинус угла φ становится равным единице:
 ;
;
2) полное сопротивление цепи  принимает минимально возможное значение и становится равным активному сопротивлению, входящему в цепь;
принимает минимально возможное значение и становится равным активному сопротивлению, входящему в цепь;
3) соответственно, ток в цепи принимает наибольшее значение
 .
.
Резкое возрастание тока в цепи при резонансе может вывести её из строя, если возможность резонанса не была предусмотрена заранее.
Частота, на которой наступает резонанс, может быть определена из формулы:

Анализируя условие возникновения резонанса можно понять, что добиться возникновения резонанса можно тремя путями:
1) меняя величину индуктивности L, что достигается перемещением ферромагнитного сердечника внутри катушки индуктивности;
2) меняя величину ёмкости С, путем подбора конденсатора;
3) меняя частоту приложенного к цепи напряжения Uоб.
Раздел 4. Трёхфазные цепи
35. Понятие трёхфазной системы ЭДС. Область применения трёхфазного тока. Достоинства трехфазного тока. Получение трёхфазной системы ЭДС.
Трехфазный ток
Основные понятия
В промышленности широко используется трехфазный синусоидальный ток. Однофазный ток, применяемый в быту, является частью трехфазной системы.
Значительный вклад в развитие трёхфазных систем внёс наш соотечественник, русский инженер, М. О. Доливо-Добровольский, который впервые предложил связанную(трёх- и четырёхпроводную) систему трёхфазного тока.
Широкое применение трёхфазного тока объясняется достоинствами трехфазной системы:
1) упрощается передача и распределение энергии от электростанции к потребителям;
2) на базе трехфазного тока создан простой, дешевый и надежный электродвигатель; это очень важное достоинство, т.к. для производства любой продукции необходим электродвигатель.
Трехфазной называется система трех одинаковых по амплитуде и частоте синусоидальных величин, смещённых по фазе на 120 градусов относительно друг друга.
Три синусоиды обозначаются буквами A, B иC и, соответственно, называются фазами A,B или С. Эти синусоиды могут изображать напряжение, ток или ЭДС.
График трехфазного напряжения показан на рис. 76. На графике изображены синусоиды трёх напряжений: uА, uBиuC.
По горизонтальной оси графика отложен фазовый угол ωt – угол поворота рамки генератора, в которой индуктируется синусоидальная ЭДС. (Повторите принцип работы и устройство генератора однофазного переменного тока.)

Рис. 76. График трехфазной системы напряжений на волновой диаграмме
Графики трёхфазной системы токов или трехфазной системы ЭДСбудутвыглядеть аналогично.
Напомним, что каждая синусоида формируется за один полный оборот рамки генератора, который составляет 360 градусов или 2π радиан.
Построение графика трёхфазного тока начинается с построения осей координат, а затем – синусоиды фазы А. Её синусоида начинается из начала координат (в точке 0).
Чтобы удобнее было строить синусоиды фазы Bи фазы С, каждый полупериод синусоиды фазы А разбит на три равные части. Полупериод синусоиды соответствует 180 градусам, следовательно в каждом отрезке будет 60 градусов.
После построения синусоиды фазы А строятся две другие синусоиды.
Положительный полупериод синусоиды фазы В начинается на 120 градусов правее начала положительного полупериода синусоиды фазы А. Это означает, что синусоида В отстаёт по фазе от синусоиды фазы А на 120 градусов.
Синусоида фазы С начинается на 120 градусов правее начала положительного полупериода синусоиды фазы В, т.е. отстаёт от синусоиды фазы В на 120 градусов. Можно также сказать, что синусоида фазы С отстаёт по фазе от синусоиды фазы А на 240 градусов.
Математически три синусоиды трёхфазной системы можно записать в виде:



На рис. 77 синусоидальные величины трёхфазной системы показаны на векторной диаграмме

Рис. 77. Изображение трехфазной системы напряжений
на векторной диаграмме
На векторной диаграмме трехфазная система напряжений, токов или ЭДС изображается в виде трех векторов, под углом 120 градусов друг к другу.
36. Конструкция генератора трёхфазного тока, отличия от конструкции генератора однофазного тока. Принцип работы генератора.






