Три одинаковых лампы накаливания включены треугольником. Сопротивление каждой лампы 484 Ом. Вольтметр показывает напряжение 220 вольт. Определить фазные и линейные токи в схеме. Найти мощность, потребляемую всей схемой.

Рис. 88. Схема к примеру 20.
Соединение ламп накаливания в треугольник
Решение
Вольтметр подключён между линейными проводами и показывает линейное напряжение. Оно в треугольнике равно фазному и равно 220В.
Сопротивление каждой фазы потребителя Rф равно сопротивлению лампы Rл. Фазные токи можно найти по закону Ома:
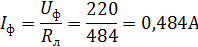
Линейный ток в каждой фазе найдём по формуле:
Iл=  Iф=1,73*0,484=1,15А.
Iф=1,73*0,484=1,15А.
Общая мощность, потребляемая схемой, равна утроенной мощности одной фазы, т.к. нагрузка равномерная:
Pоб=3Pф=3*100=300вт.
42. Формулы для определения активной мощности трёхфазной системы при равномерной и неравномерной нагрузке.
Мощность в трёхфазной системе
Активную мощность, потребляемую одной фазой трёхфазного потребителя, можно найти по формуле, рассмотренной при изучении темы "однофазный переменный ток"
Pф=Uф*Iф*cosφф
В случае равномерной нагрузки мощность всех фаз одинакова, поэтому общая мощность можно найти, утроив мощность одной фазы
Pф=3*Uф*Iф*cosφф
Если же нагрузка неравномерная, придётся вычислить мощность каждой фазы отдельно и, затем, найти сумму мощностей всех фаз
Pобщ = Pa+Pb+Pc
Для случая активной нагрузки (рис. 80), коэффициент мощности (cosφ) равен единице. Если же в фазе потребителя включена цепочка RLили RC, то коэффициент мощности можно найти по формуле
cosφ=R/Z, гдеZ = 
Пример 18. Расчёт мощности потребителя при соединении звездой
По данным примера17 определить мощность, потребляемую всеми тремя лампами
Решение:
В любой электрической схеме, в том числе в трехфазной системе, общая мощность равна сумме мощностей, потребляемых элементами схемы. Поскольку мощность каждой из ламп известна, общая мощность трёхфазной системы
Pобщ = Pa+Pb+Pc = 60+100+100 = 360Вт.
Пример 19. Расчёт тока, потребляемого трёхфазным электродвигателем, по его параметрам
Трёхфазный электродвигатель, обмотки которого соединены звездой, подключён к стандартной трёхфазной сети с линейным напряжением Uл =380 В. Частота тока в сети - 50 Гц.
Известны паспортные данные двигателя: механическая мощность двигателя 4,2 КВт, КПД=h=0,72 (72%), коэффициент мощности – cosj =0,85.
Определить: а) фазные токи, потребляемые двигателем; б) параметры обмотки двигателя.
Решение.
А) Найдем ток, потребляемый каждой обмоткой двигателя.
На статоре трёхфазного двигателя уложено три обмотки. Каждая обмотка представляет собой реальную катушку индуктивности и изображена на схеме в виде цепочки RL, т.е. как последовательное соединение активного сопротивления и индуктивности.

Рис. 86. Схема включения обмоток двигателя к примеру 19.
В паспортных данных двигателя указана механическая мощность P2 (мощность на валу двигателя). Для расчёта электрических параметров двигателя необходимо знать электрическую мощность P1, потребляемую двигателем от трёхфазной питающей сети.
Механическая (полезная) мощность P2 всегда меньше, чем электрическая мощность P1, потребляемая от сети. По формуле КПД найдем электрическую мощность, потребляемую двигателем.
КПД=h= Pмех/Pэл=P2/P1, откуда:
Рэл= Рмех /h =4200 / 0,72 = 5833 Вт.
По формуле мощности трёхфазной системы найдём ток, потребляемый одной фазой двигателя:
Iф= Iл = Рэл/ 3Uф сosj = 5833 / 3 * 220 * 0,85 = 10,4 А.
Фазное напряжение Uф, необходимое для расчётанайдено, зная соотношение между линейным и фазным напряжением, по формуле:
Uф = Uл /  =220 В.
=220 В.
Б) Находим параметры обмотки двигателя: её активное сопротивление и индуктивность.
Полное сопротивление фазы двигателя, т.е. полное сопротивление такой катушки можно найти из закона Ома для реальной катушки, зная напряжение на фазе и ток фазы:
Zф = Uф / Iф =220 / 10,4 = 21,15 Ом.
Зная соотношения для реальной катушкииндуктивности, найдём активную и реактивную составляющие полного сопротивления фазы двигателя:
Rф = Zф* cosj =21,15 * 0,85 = 18 Ом.
XL = 
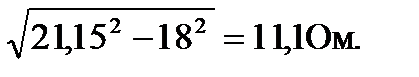
Из формулы индуктивного сопротивления катушки найдём индуктивность фазы двигателя:
L = XL/ 2pf = 11,1 / 2*3.14*50 = 0,035 Гн.






