В 1827г. английский ботаник Роберт Броун, исследуя споры папоротника в воде обратил внимание на их хаотические движения, которые зависели от их размера и температуры. Только в конце 19 в. Гуи и Экснер связали это с тепловым движением молекул. Фактически это открытие доказывало существование атомов и молекул.
Экснер попытался количественно описать эти движения, используя уравнения кинетической энергии частиц
, где k – const Больцмана.
Однако вычисления давали значения перемещений в 1000 раз превышающие экспериментальные (4000 мкм/с вместо 4мкм/с).
Это можно объяснить, используя только законы статической физики. В 1 сек. частицы испытывают до 1020 толчков и перемещение частиц является итогом их результирующего воздействия.
Теоретически броуновское движение обосновали А.Эйнштейн (1905 г.) и М.Смолуховский (1906 г.) – независимо друг от друга. Оба они приняли представление о среднем сдвиге частицы в двух координатах «x» и «y» как их проекции движения на плоскости.
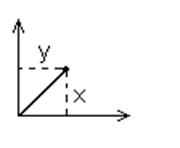
Учитывая равновероятность отклонения от осей «x» и «y» (∟45˚), имеем
, 
или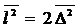 
;
Они установили также количественную связь между квадратом среднего сдвига частиц 
и коэффициентом диффузии Д.
Если представить условную плоскость, разделяющую систему на две части и при этом между ними есть некоторое концентрационное неравенство: т.е. c1 < c2, то хаотичность броуновского движения приводит к равной вероятности перехода частиц через плоскость. Половина частиц за какое-то время переместится вправо, половина влево. Соответствующие потоки могут быть рассчитаны:
,
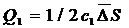Суммарный поток будет равен:
Градиент концентраций (с1 - с2) может быть выражен:
.
Подставив в выражение для суммарного потока, получим:
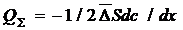
Из первого закона Фика поток частиц при диффузии равен:
Приравняв тот и другой потоки, получим уравнение Эйнштейна для диффузии:
.
В свою очередь: 
, где В – коэффициент трения.
- закон Стокса.
- закон Эйнштейна-Смолуховского.
В соответствие с законом, частицы перемещаются тем интенсивнее чем выше температура Т, время τ и меньше вязкость среды η и их радиус r.
Экспериментально это уравнение было подтверждено Сведбергом (1909), Перреном (1910), Бойлем (1909), Милликеном (1910).
Сведберг – измерял сдвиг частиц коллоидного золота от τ и η. Полученные результаты подтвердили справедливость закона.
Перрен - экспериментально, используя систему гуммигут - H2O, с высокой точностью определил число Авогардо NA.
Бойль, используя закон Эйнштейна-Смолуховского, определил заряд частиц аэрозоля табачного дыма.
Милликен, используя систему масляного тумана, экспериментально очень точно определил заряд электрона.
ВЫВОДЫ:
Доказательство справедливости закона Эйнштейна-Смолуховского для коллоидных систем привела к фундаментальным выводам о применимости к истинным коллоидным системам законов молекулярно-кинетической теории, законов связанных с энтропией, т.е. коллоидные системы обладают свойствами гетерогенно-дисперсных систем и истинных растворов.
Поверхностное натяжение
Почему по водной поверхности бегают пауки-шагомеры? Почему металлическая игла удерживается на водной поверхности?
Почему англичане в XVII – XVIII вв. выливали в бушующее море тюлений или китовый жир для того, чтобы избежать кораблекрушения? Как норвежские рыбаки определяли место косяка сельди? Ответы на эти вопросы могут быть даны, если понять, что такое поверхностное натяжение.
Еще раз посмотрим на энергетическое положение атома в объеме тела и на его поверхности.
А. В объеме тела связи атомов уравновешены и 
| Б. На поверхности атом не имеет «соседей» с одной стороны. В результате результирующая сила  и направлена внутрь тела
|
| 
|
Втягивая поверхностные атомы внутрь, тело как бы стремится уменьшить свою поверхность. На поверхности возникает напряжение, характеризующееся наличием избыточной энергии из-за нескомпенсированности взаимодействия поверхностных атомов.
1.Избыточная поверхностная энергия приходящаяся на единицу площади поверхности получила название поверхностного натяжения (σ) 
.
Физическая природа σ в нескомпенсированности поля межмолекулярных сил на межфазной поверхности.
2. Поверхностное натяжение можно также трактовать как силу, действующую тангенциально поверхности (вдоль нее) и препятствующую увеличению поверхности.
3. σ – можно также рассматривать как работу, затраченную на разрыв межатомных или межмолекулярных связей, т.е. это работа образования единицы поверхности. На σ влияют T, q (заряд поверхности), добавки ПАВ.
[σ]=Дж/м2; Нм/м2=Н/м. В СГС: дин/см; 1 Н/м=1000 дин/см
Чем сильнее межмолекулярные связи в веществе, тем больше σ на его межфазной поверхности.
Для H2O σ = 0,0721 Дж/м2
для C2H5OH 0,0221 Дж/м2
для Hg 0,473 Дж/м2
для Fe 4,0 Дж/м2
для W 6,8 Дж/м2
для алмаза 11,4 (максимальное значение для известных веществ).
Для твердых тел обычно говорят об удельной поверхностной энергии.
