Вопрос об оптимальных весовых коэффициентах при определении вклада каждого задания в итоговый балл ученика решается по-разному. Большинство специалистов склоняются к выводу о преимуществе дихотомической оценки по результатам выполнения каждого задания теста. При этом ученик получает 1 за правильное выполнение задания и 0 за пропуск либо неверный ответ. Сторонники дихотомической оценки руководствуются весьма простым соображением, подкрепленным соответствующими математическими выкладками [45]. Проигрыш в точности измерений будет существенно меньше, если ограничиться дихотомической оценкой, а весовыми коэффициентами, выбранными на основе субъективных суждений экспертов либо субъективных представлениях автора.
Распространенный в нашей стране подход к выбору весовых коэффициентов основан на подсчете числа шагов, необходимых для выполнения задания теста. Логика сторонников этого подхода примерно такова: чем больше шагов требуется для выполнения задания, тем больше должен быть вклад задания в общую оценку по тесту.
Вполне понятны основания для критики, поскольку налицо явный формализм в оценке вклада в итоговый балл каждого задания теста. При такой постановке вопроса сумма большого количества простых шагов при выполнении задания, требующего репродуктивного уровня деятельности, может давать больший вклад, чем один довольно трудный шаг, предполагающий элементы творческой деятельности при выполнении задания теста.
Еще один тупиковый путь основан на выборе весовых коэффициентов, пропорциональных определенной статистическим путем трудности заданий теста. Эти весовые коэффициенты ничего не дают для повышения эффективности тестовых оценок сильных учеников, но могут привести к значительному росту ошибки измерения при оценке наиболее слабых учеников в тестируемой группе. Слабый ученик, угадавший правильный ответ к нескольким наиболее трудным заданиям, может по результатам тестирования выглядеть значительно лучше, чем другие, более сильные, не использующие угадывания при выполнении заданий теста. В этой связи в исследованиях Ф. Лорда предполагается присваивать нулевые или близкие к нулевым весовые коэффициенты для наиболее трудных заданий при подсчете баллов слабых учеников по результатам выполнения теста.
В результате многолетней работы ряда зарубежных исследователей удалось в рамках IRT создать специальное обоснование проблемы выбора оптимальных весовых коэффициентов к заданиям теста. Достаточно подробно это обоснование изложено в [46].
Обоснование построено на определении весовых коэффициентов из условия максимизации значений информационной функции теста (см. разд. 5.3). В результате сложных выкладок Р.К. Хэмблтон приходит к интересному результату. Оптимальные весовые коэффициенты должны находиться по формуле

где со—весовой коэффициент j-го задания; Pi — производная по переменной 9 от функции Р., задающей вероятность правильного ответа на j-е задание теста; Q,= 1 — Р.— вероятность неправильного ответа на j-е задание теста.
В зависимости от выбранной математической модели, аппроксимирующей Р j и Qj, весовые коэффициенты имеют вид, представленный в табл. 5.26.
Таким образом, исходя из результатов табл. 5.26, можно сделать вывод, что при использовании однопараметрической модели и описанных в разд. 5.3 алгоритмов для оценки значений Qi (i= 1,2,..., N) лучше всего применять не взвешенные оценки и считать сырой балл каждого ученика по формуле
Таблица 5.26. Оптимальные весовые коэффициенты для логических моделей IRT
| Модель | 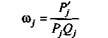
| Комментарий |
| Однопараметрическая модель Г. Раша | 
| со, не зависит от 9 |
| Двухпараметрическая модель А. Бирнбаума | 
| Юу не зависит от 9 |
| Трехпараметрическая модель А. Бирнбаума | 
| со, является функцией от переменной 9, так как
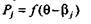
|

а затем вычислять Qi, по описанным в разд. 5.3 алгоритмам.
Для двухпараметрической модели вклад каждого задания в сырой итоговый балл должен быть пропорционален а j:
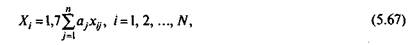
где параметр u j — дифференцирующая способность j-го задания теста.
Для трехпараметрической модели оптимальные весовые коэффициенты должны зависеть не только от параметров заданий, но и от уровня подготовки оцениваемого ученика. В соответствии с рекомендациями Ф. Лорда [50] для сильных учеников весовые коэффициенты стремятся к aj Этот вывод легко получить из последней формулы для весовых коэффициентов в табл. 5.26:

Однако для сильного ученика вероятность правильного ответа на j-е задание стремится к единице (Pj -> 1), поэтому формулу (5.68) можно переписать в виде

Для слабого ученика, наоборот, при выполнении трудных заданий Р.—> с,, поэтому wj -> 0, так как

Идеи Лорда были развиты А. Бирнбаумом, который построил специальные кривые для выбора оптимальных весовых коэффициентов (рис. 5.38).
На рис. 5.38 по горизонтальной оси откладываются значения 6, по вертикальной — значения wj. Кривая 1 соответствует заданию с низким значением параметра дифференцирующей способности (a1 < 0,5). Поэтому вклад этого задания в общую оценку невелик как для сильных, так и для слабых учеников. Кривые 2 и 4 соответствуют довольно трудным заданиям (а4 > а2), поэтому при низких значениях 0 вклад заданий 2 и 4 в итоговый балл слабых учеников близок к нулю. По мере роста значений 0 на первый план выходит величина а,. Задание 4 с большим значением о4 при подсчете баллов сильных учеников будет иметь больший весовой коэффициент. И наконец, заданию 3 соответствует умеренно пологая кривая (а3~ 1), но оно имеет небольшую трудность, поэтому весовые коэффициенты для этого задания отличны от нуля даже для самых слабых учеников.
Таким образом, вопрос выбора оптимальных весовых коэффициентов достаточно сложен. Для его научного решения необходимо использование математического аппарата IRT и специальных математических теорий. При больших значениях 0 оптимальные весовые коэффициенты пропорциональны дифференцирующей способности заданий. Для малых Q и больших b оптимальные весовые коэффициенты близки к нулю.
В заключение уместно привести некоторые рекомендации по отбору заданий в тест. Конечно, такие рекомендации могут носить самый общий характер, поскольку при отборе заданий есть довольно много разнообразных факторов, а при окончательном решении их следует разумно уравновесить. Несомненно, наиболее эффективны задания со значениями параметра трудности bв интервале (0,20; 0,80), поэтому именно их в первую очередь следует включать в тест. Однако, если в этот интервал попадают задания с низкой дискриминативностью, а другие, с высокой дискриминативной способностью, имеют трудность 0,18, то именно последним заданиям следует отдать предпочтение при отборе заданий в тест.

Рис. 5.38. Кривые оптимальных весовых коэффициентов






