| i | Оценка Qi |
| 3 | -3,60457 |
| 2 | -2,29834 |
| 5 | -0,71843 |
| 6 | -0,71843 |
| 8 | -0,71843 |
| 7 | -0,06531 |
| 1 | 0,58781 |
| 10 | 0,58781 |
| 9 | 3,47395 |
| 4 | 3,47395 |
Если Qi и bi выбраны неудачно, довольно далеко от оценок наибольшего правдоподобия, то число итераций увеличится. Соответственно возрастут и затраты машинного времени.
Кроме других, менее очевидных условий, на удачный выбор начального приближения для 0 оказывает решающее влияние наличие банка тестовых заданий, шкалированных по нарастанию трудности, с известными устойчивыми значениями р. Такой банк дает возможность преподавателю предложить i-му ученику оптимальные по трудности задания, обеспечивающие оценку 0(. с минимальной стандартной ошибкой измерения.
На идее минимизации ошибки измерения строится понятие информационной функции, введенное А. Бирнбаумом в 1968 г. для оценки эффективности каждого задания и всего теста при измерении значений переменной 0.
Информационные функции. Наиболее сильный аргумент в пользу современной теории создания тестов (IRT) связан с введением информационной функции, которая используется для оценки эффективности теста. В отличие от классической теории, не позволяющей повысить эффективность тестовых измерений, в IRT можно ставить вопрос о дифференцированной оценке эффективности j-го задания теста для оценки каждого значения 0. Это преимущество связано с возможностями математического аппарата IRT, позволяющего вычислить дифференцированную стандартную ошибку измерения.
Процесс повышения эффективности теста связан с подбором наиболее пригодных заданий, обеспечивающих минимальное отклонение начальной оценки Qi0 от истинного значения Qi. Степень пригодности принято характеризовать с помощью относительной величины, называемой информацией. По одному из определений, предложенных А. Бирнбаумом [50], количество информации, обеспеченное j заданием теста в данной точке Qi, — это величина, обратно пропорциональная стандартной ошибке измерения данного значения Qi с помощью задания j.
Так как каждому значению Qi ставится в соответствие некоторое количество информации, получаемой при оценивании параметра с помощью задания j то можно ввести в рассмотрение специальную функцию. Значения этой функции являются своеобразной характеристикой j-го задания в каждой точке оси латентной переменной 0. Чем больше количество информации, тем лучше, образно говоря, работает задание на рассматриваемом интервале оси Q.
На введенном определении основан вывод формулы для подсчета значений информационной функции j -го задания при различных значениях независимой переменной 0. Вне зависимости от используемой модели информационную функцию j-го задания теста I(Q) можно записать как в [31,46].
где все обозначения прежние, а функции Р i и Qj зависят от переменной 0.
Для однопараметрической модели (5.14) Prj=1.7PJQj(см. вывод в приложении 5.7), и поэтому
где Qj = 1 - Pj является вероятностью неправильного ответа учеников на j-е задание теста.
Для двухпараметрической модели (5.16)
где а, — дифференцирующая способность j - ro задания теста и
Qj=l-Pj
Вывод формулы (5.49) аналогичен приведенному в приложении 5.7.
Для трехпараметрической модели информационная функция j-го задания имеет вид
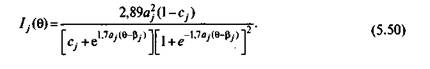
Вывод этой формулы в силу сложности в работе не приводится.
Можно отметить ряд свойств информационной функции j- го задания теста, основанных на формуле (5.47). Прежде всего следует обратить внимание на производную в числителе дроби, где дифференцирование ведется по переменной Q. Очевидно, что при увеличении числителя значение дроби увеличивается. Максимальное значение производной Pj(Q ) достигается в точке перегиба характеристической кривой j-го задания теста, там, где касательная образует с осью Q наибольший угол. Так как точке перегиба графика функции Pj(Q ) соответствует значение Q = (bj) то первое наиболее важное свойство можно сформулировать так: для измерения данного значения латентной переменной Qi наиболее информативны задания с трудностью
Существенно, что применяемый в этом случае математический аппарат позволяет определить, насколько информативно задание, какова мера его эффективности при измерении данного 0 по сравнению со стопроцентным уровнем, достигаемым при Q = b.
Геометрическая интерпретация позволяет выделить в качестве наиболее эффективных задания со значениями b в окрестности точки Qi оси Q. Удобнее всего рассмотреть разность Qi— b. Чем ближе значение разности к нулю, чем меньше расстояние, на котором находятся задания от значения Qi, тем эффективнее подобрано задание, тем меньше стандартная ошибка измерения данного значения Qi.
Второе свойство связано с особенностями введенного понятия информации, позволяющего в отличие от классической теории тестов оценивать независимые вклады каждого задания в общую оценку 0. Благодаря свойству независимости можно сделать вывод, что для оценки тестируемого порядок расположения заданий в тесте не играет роли. Но это вовсе не означает, что задания могут предлагаться тестируемому в случайном порядке и принцип нарастания трудности не должен соблюдаться. Разумеется, это свойство имеет более теоретическое, чем практическое значение. Как правило, тесты с различным порядком предъявления заданий дают различные эмпирические результаты.
Значение параметра b — не единственный критерий, учитываемый при выборе оптимальных заданий для тестирования каждого испытуемого. Следующее важное свойство связано со вторым параметром j-го задания — параметром af Так как значение af прямо
пропорционально Pj, то третье свойство вносит дополнительную информацию в критерий отбора оптимальных заданий для эффективного измерения данного значения Qi.
Основываясь на третьем свойстве, можно предположить, что наиболее информативны задания с более крутыми характеристическими кривыми. Чем круче кривая, тем больше вклад задания в измерение данного значения Qi. Однако, стремясь включить в тест задания с наиболее крутыми характеристическими кривыми, можно совершить ошибку и прийти к снижению эффективности измерения в отдельных точках оси Q за счет неоправданного ее увеличения в других точках этой же оси.
Дело в том, что рост крутизны характеристической кривой помимо положительных эффектов сопровождается и отрицательными. Последние связаны с уменьшением длины интервала оси 0, обеспечивающей хорошую дифференциацию индивидуальных различий испытуемых. Этот отрицательный эффект характерен для значений Q, лежащих по одну сторону от точки перегиба кривой. Чем круче кривая задания, тем меньше различаются значения вероятностей правильного выполнения задания в таких точках. Поэтому при отборе заданий для теста нужен дополнительный анализ, учитывающий характер распределения значений латентной переменной в и вклад всех заданий в суммарную информацию для каждой точки оси 0.
Благодаря свойству аддитивности информация, полученная при измерении данного 0 с помощью всего теста, складывается из отдельных составляющих Ii(Qi) (i=1, 2,..., n). Тогда для всего теста
где I(Q) — информационная функция теста, состоящего из п заданий. С учетом формулы (5.47) можно записать
Знак производной в числителе дроби подразумевает наличие предельного перехода, поэтому число заданий в тесте должно быть достаточно большим. Количество заданий влияет и на форму графика функции I(Q). Если количество заданий меньше 25 [50], то график информационной функции теста не имеет одного четко выраженного максимума. В этом случае можно говорить о снижении эффективности всего теста в целом. Например, наличие двух точек максимума указывает на необходимость дальнейшей работы с тестом.
На рис. 5.29 приведен график функции I(Q), имеющей две точки максимума (кривая I). Анализ формы информационной кривой указывает по меньшей мере на два возможных направления дальнейшей работы с тестом. Если число заданий невелико, то необходимо добавлять задания со значениями параметра трудности в интервале Q1 < b < Q2, изменяя форму кривой в сторону увеличения ее выпуклости с четко выраженным максимумом в одной из точек оси 0.
Если число заданий достаточно велико (n > 100), то исходный тест лучше разбить на два, один из которых будет эффективен для выборки со средним значением Q вблизи точки Q1, а другой — для выборки испытуемых с Q ~ Q2.
При выборе заданий определенной трудности из банка следует ориентироваться на среднее значение 0, вокруг которого распределятся наибольшее число значений латентного параметра тестируемых учеников; формирование четко выраженного максимума на информационной кривой должно идти в основном за счет добавления заданий со значениями параметра в окрестности точки
0. Это повысит эффективность вновь созданного теста на выбранном интервале оси латентной переменной.
Кривая 2 на том же рисунке принадлежит менее информативному тесту, проигрывающему по сравнению с первым при оценке выборки учеников, расположенных вблизи точки Q2. Однако у второй кривой есть и явное преимущество. Она имеет один четко выраженный максимум, что и позволяет отдать ей предпочтение при сравнительном анализе качества первого и второго тестов. Третья пологая кривая принадлежит явно неудачному тесту, который является малоинформативным на всем протяжении оси Q.
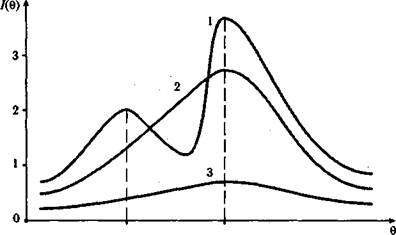
Рис. 5.29. Информационные кривые трех тестов
Для однопараметрической модели построение информационной функции
j -го задания осуществляется путем подсчета значений функции Ij(0) по формуле (5.48), которую следует переписать в более удобном для вычислений виде:
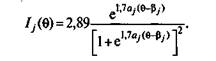
Меняя различные значения независимой переменной 9, можно получить различные точки графика /.(0).
Графики информационных функции 10 заданий рассматриваемого примера матрицы из табл. 5.3 приведены на рис. 5.30.
После суммирования отдельных ординат кривых получится график, изображенный на рис. 5.31.
Для двухпараметрической модели функция теста имеет вид [46]
Информационные функции заданий в случае, когда Р j (Q) имеет только один или два параметра (выражения (5.14) и (5.16)), имеют максимум при Q = b.
Несложный анализ формулы для подсчета значения Qmax, соответствующего точке максимума информационной функции в случае трехпараметрической модели (5.18), помогает убедительно обосновать практические преимущества тестовых заданий в открытой форме. Согласно этой формуле [46]
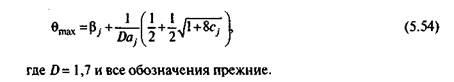
| 10 |
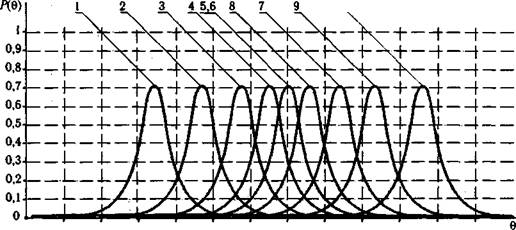Рис. 5.30. Графики информационных функций десяти заданий теста
Рис. 5.31. График информационной функции теста
Вычисление значений I(Qmax) для различных с указывает на рост количества информации при убывании с j: максимального значения IQmax) достигает при с = 0. Таким образом, включение в тест заданий в открытой форме повышает информативность теста в каждой точке оси латентной переменной Q. Закрытые задания с двумя ответами (Cj = 0,5), наоборот, сильно снижают эффективность тестовых оценок.
Конечно, аппарат IRT довольно сложен, и поэтому начинать разработку теста следует, основываясь на классической теории, несмотря на ее низкую эффективность и существенные недостатки.
Если же при разработке теста намечается провести более точное и эффективное измерение значений в, требующее предварительного создания банка тестовых заданий с известными устойчивыми значениями параметра трудности, то привлекается специальный математический аппарат, рассмотренный в следующем разделе. В этом случае тест моделируется для эффективного оценивания каждого значения Q. Одно и то же задание может оказаться как эффективным, так и неэффективным при измерении различных значений Q. Поэтому не существует единой оптимальной модели при отборе заданий в тест. Предлагаемое моделирование позволяет целенаправленным подбором заданий для оценивания данного Qi. лишь минимизировать стандартную ошибку измерения его значения.
Конструирование тестов на продвинутом этапе. Продвинутый этап разработки тестов в отличие от начального предполагает наличие банка тестовых заданий с известными значениями параметра b.
Предварительно разработчик, ориентируясь на свойства выборки испытуемых, задается желательной формой информационной кривой вновь создаваемого теста. Дальнейший процесс формирования теста можно разбить на ряд шагов:
• построение гипотетической информационной кривой теста, обеспечивающей заданную стандартную ошибку измерения в нужном интервале оси 6;
• построение графиков информационных кривых заданий из банка тестовых заданий, имеющегося в распоряжении разработчика;
• выбор заданий с информационными кривыми, удовлетворительно заполняющими пространство под планируемой информационной кривой теста;
• сложение ординат кривых тестовых заданий в каждой точке оси латентной переменной 0;
• продолжение процесса выбора заданий до тех пор, пока площадь под гипотетической кривой не будет заполнена с заданной степенью точности;
• проверка абсолютного значения разности между максимальной суммой ординат кривых заданий и планируемым максимумом на гипотетической кривой в точке Qmax.
Если в результате выполнения всех этапов заданная степень точности не достигнута, следует добавить задания из банка и повторно оценить достигнутую степень точности для точки максимума на гипотетической кривой.
Вычислив значения информационных функций, можно сравнить эффективность различных вновь созданных тестов с исходным без предварительного сбора эмпирических данных. Предположим, что два теста Х и Y оценивают одно и то же скрытое качество — латентную переменную 6. Сравнительную эффективность теста У по отношению к тесту X можно охарактеризовать специальной функцией Е(Y, X), значения которой равны отношению значений информационных функций тестов У и Х в соответствующих точках оси Q [31,47]:
Функция Е (Y, X) получила название функции сравнительной эффективности. Особый интерес представляет свойство инвариантности функции Е (Y, X) относительно метрики, выбранной для измерения 0 в первом и втором тестах.
Вычисление значений E (Y, X) позволяет оценить эффект при удалении из теста заданий определенной трудности, при замене заданий средней трудности на легкие или более трудные, а также решить ряд других вопросов, возникающих у опытного создателя тестов.
Практическое применение функции сравнительной эффективности иллюстрирует рис 5.32, на котором представлены три функции Е1,Е2, Е3 для трех различных тестов, два из которых (кривые 1 и 2) образованы из начального теста (50 заданий), а третий получен путем добавления дополнительных заданий из банка (кривая 3). По горизонтальной оси откладываются индивидуальные баллы испытуемых группы, по вертикальной — значения функции сравнительной эффективности для данного теста и трех вновь созданных. Горизонтальная прямая Е = 1 соответствует начальному тесту из 50 заданий.
В первый тест войти 25 наиболее трудных заданий из 50, данных вначале. Кривая 1 функции Е1 расположена всюду ниже горизонтальной прямой, соответствующей начальному тесту. Следовательно, первый тест половинной длины из наиболее трудных заданий оказался менее эффективным, чем начальный для всех испытуемых со значениями латентного параметра в любой точке оси 6.
Кривая 2, соответствующая функции Е2, позволяет сравнить эффективность второго теста, составленного из 25 наиболее легких заданий, с эффективностью данного из 50 заданий. Анализ формы кривой 2 выявляет снижение эффективности при тестировании хорошо подготовленных испытуемых в группе по сравнению с начальным полным набором заданий. Наоборот, для испытуемых с низкими индивидуальными баллами второй тест более эффективен. Этого, вообще говоря, следовало ожидать, так как эффект угадывания ответов на наиболее трудные задания снижает информативность второго теста.
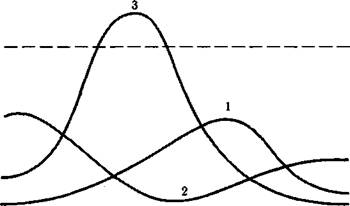
Рис. 5.32. Графики функций сравнительной эффективности
Кривая 3 соответствует тесту, составленному из 50 заданий, но не данных, а дополнительно привлеченных из банка, большая часть которых имеет приблизительно среднюю трудность. Этот тест гораздо эффективнее, чем данный, для испытуемых со средними значениями индивидуальных баллов.
При моделировании теста обычно задаются гипотетической желаемой областью, обеспечивающей высокую информативность оценок Q на том участке, где расположена тестируемая выборка учеников, как, например, на рис. 5.33. Затем начинают подбирать задания из банка, используя функцию из формулы (5.55) для оценки сравнительной эффективности моделируемого теста.
Таким образом, рассмотренная функция сравнительной эффективности позволяет моделировать тест без сбора дополнительной эмпирической информации. Предоставленный аппарат для конструирования эффективных тестов призван помочь преподавателям в их практической работе и научиться оценивать эффективно знания учеников любой выборки.
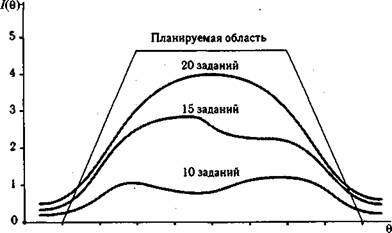
Рис. 5.33. Информационные кривые моделируемых тестов
