После обработки тестовых данных и интерпретации результатов обработки предтестовые задания обретают статус тестовых. Правда, в категорию тестовых попадают не все, а только те, которые обладают хорошими статистическими характеристиками. Процедура выявления характеристик получила название анализа заданий (Item Analysis) [59]. В общем случае она включает оценку трудности задания, его корреляции с другими заданиями и общим показателем по тесту, факторный анализ, шкалирование заданий с помощью аппарата IRT и определение некоторых других характеристик.
Первая, наиболее важная характеристика — это трудность заданий теста.
Трудность тестовых заданий. Оценка трудности тестовых заданий проводится по-разному в зависимости от выбранной теории методов обработки эмпирических результатов выполнения теста. В классической теории оценка трудности j-го задания получается по формуле

где pj — доля правильных ответов на j-е задание; R. — количество учеников, выполнивших j - e задание верно; N — число учеников в тестируемой группе; j— номер задания теста.
В тесте из п заданий у принимает значения j = 1, 2,..., п. Трудность задания нередко выражают в процентах, тогда формула для оценки трудности имеет вид

где Р j — трудность в процентах.
Без сомнения, долю правильных ответов на задание р. естественно интерпретировать как легкость задания. В то время как трудность скорее ассоциируется с долей неправильных ответов qj, которая находится путем вычитания pj из единицы:

Однако по сложившейся традиции в рамках классической теории тестов за трудность задания принимается именно доля р..
Для примера матрицы из табл. 5.3 доля правильных ответов на первое задание
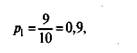
а доля неправильных ответов ql = 1-0,9 = 0,1 и т. д.

После перевода доли b j в проценты 0,9 • 100% = 90% первое задание следует отнести к категории крайне легких: его выполнили примерно 90% тестируемой выборки учеников.
В рамках IRT трудность задания р. выражают в виде натурального логарифма дроби

(подробнее см. в разд. 5.3).
Представление о трудности заданий теста легко получить путем анализа гистограммы, такой, как, например, на рис. 5.34.
В рассматриваемом примере (не относящемся к матрице из табл. 5.3) гистограммы явно просматриваются недостатки в подборе по трудности заданий теста. Первый недостаток связан с тем, что задания не ранжированы по нарастанию трудности так, как обычно рекомендуется располагать задания в итоговых тестах. Тест начинается с трудного первого задания, которое смогли выполнить всего 10% учеников. Затем идет второе, тоже довольно трудное задание (р2= 20%). Третье задание — слишком легкое: с ним справились все без исключения, и четвертое — тоже довольно легкое: его выполнили верно 90% учеников и т.д. Второй недостаток—отсутствие заданий средней трудности ср- 0,5. Конечно, при отборе предтестовых заданий в процессе формирования теста разработчик вовсе не планировал такую гистограмму, как на рис. 5.34. Он думал, что располагает задания по нарастанию трудности, которая для большинства заданий, по его мнению, была близка к 50%. Тем не менее наделе, как этого и следовало ожидать, предполагаемые начальные оценки трудности заданий, основанные на субъективных суждениях автора теста, оказались далеки от статистических, полученных на выборке учеников.
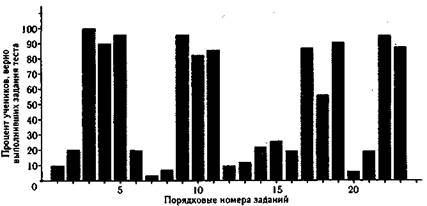
Рис. 5.34. Гистограмма трудности заданий теста
Конечно, рассматриваемый пример носит чисто гипотетический характер, однако все положения, развиваемые на нем, применимы к реальной ситуации разработки теста. Такая ситуация, как на рис. 5.34, в практике создания тестов наблюдается довольно редко. Обычно после первой эмпирической проверки автор получает распределение заданий по трудности, подобное приведенному на рис. 5.35, где встречаются задания самой разной трудности, в том числе и ср = 0,5.
Хорошо сбалансированный по трудности тест показан на рис. 5.36.
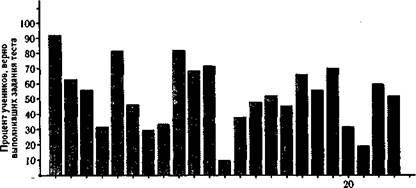
Рис. 5.35. Типичная гистограмма трудности заданий теста в начале работы

Рис. 5.36. Гистограмма хорошо сбалансированного по трудности теста
Таким образом, правильно сконструированный тест не может состоять только из легких или только из трудных заданий. Он включает всякие, самые различные по трудности задания. Хотя это правило нужно учитывать уже на начальном этапе создания теста, полагаться следует только на эмпирические оценки, а не на свое видение трудности заданий теста.
В хорошо сбалансированном по трудности тесте есть несколько самых трудных заданий со значениями р -» 0. Есть несколько самых легких с р -» 1. Остальные задания по значениям р занимают промежуточное положение между этими крайними ситуациями и имеют в основном трудность 60-70%. Таким образом, основная масса заданий по трудности приближается к середине распределения, как на рис. 5.37, отражающем нормальный закон.
Еще один аргумент в пользу преимущественного включения заданий средней трудности с р = 0,5 связан с подсчетом дисперсии по каждому заданию теста

Так как произведение pjqj д. достигает максимального значения (0,5 • 0,5 = 0,25) при р.- 0,5 = q,, то в рамках нормативно-ориентированного подхода наиболее удачными считаются задания средней трудности р = q = 0,5, обеспечивающие максимальный вклад в общую дисперсию теста.
И наконец, в пользу преимущественного выбора заданий средней трудности свидетельствует подсчет ошибки измерения, которая уменьшается по мере продвижения к центру распределения, где расположены задания средней трудности, и увеличивается на концах.

Рис. 5.37. Типичное распределение по трудности заданий теста
Правдоподобность дистракторов (для закрытых заданий). Оценка правдоподобности дистракторов основана на подсчете долей испытуемых, выбравших каждый неправильный ответ. Например, если группа из 100 испытуемых выполняла j-е задание теста с пятью ответами, из которых один верный, и 60 испытуемых выполнили задание верно, то р.= 0,6. Оставшиеся 40 испытуемых должны были равномерно распределиться между четырьмя дистракторами. Тогда распределение долей ответов на задание должно выглядеть следующим образом (табл. 5.22) (звездочкой отмечен верный ответ).
Таблица 5.22. Распределение долей испытуемых между ответами на задание теста
| Номер задания | 1-й ответ | 2-й ответ | 3-й ответ* | 4-й ответ | 5-й ответ |
| j | 0,1 | 0,1 | 0,6 | 0,1 | 0,1 |
Конечно, реальные результаты на практике редко совпадают с описанной гипотетической, идеализированной ситуацией. Даже у опытных авторов в заданиях сплошь и рядом встречаются неправдоподобные дистракторы, которые по результатам эмпирической проверки приходится менять. Анализ правдоподобности дистракторов, проведенный в реальной ситуации по результатам выполнения 42 заданий теста выборкой из 100 испытуемых, показан в табл. 5.23. В первом столбце табл. 5.23 помещены номера заданий
Таблица 5.23. Анализ правдоподобности дистракторов
| Номер задания | Всего | Распределение ответов тестируемых | |||||||
| 1-й ответ | 2-й ответ | 3-й ответ | 4-й ответ | ||||||
| тест. | % | тест. | % | тест. | % | тест. | % | ||
| 1 | 96 | 8 | 8,2 | 1 | 1,0 | 65 | 67,0* | 22 | 23,0 |
| 2 | 96 | 4 | 4,1 | 20 | 21,0 | 2 | 2,1 | 70 | 72,0* |
| 3 | 97 | 13 | 13,0 | 73 | 75,0* | 6 | 6,2 | 5 | 5,2 |
| 4 | 97 | 19 | 20,0 | 29 | 30,0 | 24 | 25,0* | 25 | 26,0 |
| 5 | 95 | 20 | 21,0* | 42 | 43,0 | 22 | 23,0 | И | 11,0 |
| 6 | 97 | 0 | 0,0 | 6 | 6,2 | 91 | 94,0* | 0 | 0,0 |
| 7 | 97 | 5 | 5,2 | 80 | 82,0* | 4 | 4,1 | 8 | 8,2 |
| 8 | 95 | 16 | 16,0 | 28 | 29,0 | 25 | 26,0 | 26 | 27,0* |
| 9 | 97 | 18 | 19,0 | 2 | 2,1 | 71 | 73,0* | 6 | 6,2 |
| 10 | 96 | 13 | 13,0 | 12 | 12,0 | 64 | 66,0* | 7 | 7,2 |
| 11 | 97 | 3 | 3,1 | 62 | 64,0* | 17 | 18,0 | 15 | 15,0 |
| 12 | 93 | 18 | 19,0 | 10 | 10,0 | 59 | 61,0* | 6 | 6,2 |
| 13 | 96 | 47 | 48,0 | 33 | 34,0* | 9 | 9,3 | 7 | 7,2 |
| 14 | 95 | 41 | 42,0 | 37 | 38,0* | 10 | 10,0 | 7 | 7,2 |
| 15 | 94 | 9 | 9,3 | 3 | 3,1 | 25 | 26,0 | 57 | 59,0* |
| 16 | 97 | 2 | 2,1 | 2 | 2,1 | И | 11,0 | 82 | 85,0* |
| 17 | 96 | 32 | 33,0 | 59 | 61,0* | 2 | 2,1 | 3 | .3,1 |
| 18 | 95 | 17 | 18,0 | 11 | 11,0 | 20 | 21,0 | 47 | 48,0* |
| 19 | 95 | 2 | 2,1 | 4 | 4,1 | 85 | 88,0* | 4 | 4,1 |
| 20 | 95 | 26 | 27,0* | 12 | 12,0 | 43 | 44,0 | 14 | 14,0 |
| 21 | 92 | 11 | 11,0 | 11 | 11,0 | 49 | 51,0* | 21 | 22,0 |
| 22 | 89 | 18 | 19,0 | 22 | 23,0 | 15 | 15,0 | 34 | 35,0* |
| 23 | 90 | 60 | 62,0* | 9 | 9,3 | 15 | 15,0 | 6 | 6,2 |
| 24 | 85 | 26 | 27,0 | 19 | 20,0* | 13 | 13,0 | 27 | 28,0 |
| 25 | 90 | 19 | 20,0 | 24 | 25,0 | 40 | 41,0* | 7 | 7,2 |
| 26 | 97 | 35 | 36,0 | 23 | 24,0 | 39 | 40,0* | 0 | 0,0 |
| 27 | 93 | 3 | 3,1 | 11 | 11,0 | 2 | 2,1 | 77 | 79,0* |
| 28 | 97 | 36 | 37,0 | 18 | 19,0 | 36 | 37,0* | 7 | 7,2 |
| 29 | 89 | 4 | 4,1 | 21 | 22,0* | 61 | 63,0 | 3 | 3,1 |
| 30 | 91 | 68 | 70,0* | 7 | 7,2 | 5 | 5,2 | 11 | 11,0 |
| 31 | 90 | 3 | 3,1 | 3 | 3,1 | 25 | 26,0* | 59 | 61,0 |
| 32 | 90 | 12 | 12,0 | 17 | 18,0 | 20 | 21,0 | 41 | 42,0* |
| 33 | 91 | 8 | 8,2 | 63 | 65,0* | 6 | 6,2 | 14 | 14,0 |
| 34 | 87 | 29 | 30,0* | 24 | 25,0 | 23 | 24,0 | 11 | 11,0 |
| 35 | 93 | 8 | 8,2 | 11 | 11,0* | 50 | 52,0 | 24 | 25,0 |
| 36 | 90 | 13 | 13,0 | 68 | 70,0* | 6 | 6,2 | 3 | 3,1 |
| 37 | 92 | 35 | 36,0 | 38 | 39,0 | 7 | 7,2 | 12 | 12,0* |
| 38 | 86 | 31 | 32,0 | 1 | 1,0 | 22 | 23,0 | 32 | 33,0* |
| 39 | 92 | 71 | 73,0* | 5 | 5,2 | 8 | 8,2 | 8 | 8,2 |
| 40 | 92 | 32 | 33,0 | 45 | 46,0* | 9 | 9,3 | 6 | 6,2 |
| 41 | 86 | 39 | 40,0* | 35 | 36,0 | 5 | 5,2 | 7 | 7,2 |
| 42 | 88 | 3 | 3,1 | 9 | 9,3 | 27 | 28,0 | 49 | 51,0* |
Таблица 5.24. Значения коэффициента точечно-бисериальной корреляции
| Задание | 1-й ответ | 2-й ответ | 3-й ответ | 4-й ответ |
| 1 | -0.1 | -0,2 | 0,3* | -0,2 |
| 2 | -0,2 | -0,3 | -0,2 | 0,4* |
| 3 | -0,3 | 0,4* | -0,3 | -0,1 |
| 4 | -0,2 | 0,3 | ОД* | -0,2 |
| 5 | 0,3* | 0,0 | -0,1 | -0,2 |
| 6 | -0,1 | 0,1* | ||
| 7 | -0,2 | 0,2* | 0,1 | -0,2 |
| 8 | -0,1 | 0,2 | -0,1 | 0,0* |
| 9 | -0,2 | 0,0 | 0,3* | -0,2 |
| 10 | -0,1 | -0,3 | 0,3* | -0,1 |
| 11 | 0,0 | 0,4* | -0,3 | -0,2 |
| 12 | -0,2 | 0,0 | 0,3* | 0,0 |
| 13 | -0,3 | 0,2* | 0,0 | 0,3 |
| 14 | -0,4 | 0,5* | 0,0 | 0,0 |
| 15 | 0,1 | -0,2 | 0,1 | 0,0* |
| 16 | -од | -0,2 | -0,3 | 0,4* |
| 17 | 0,1 | -0,1* | 0,0 | од |
| 18 | -0,3 | 0,0 | -0,0 | 0,2* |
| 19 | -0,1 | -0,2 | 0,4* | -0,2 |
| 20 | 0,1* | -0,1 | 0,1 | -0,2 |
| 21 | -0,3 | -0,2 | 0,4* | 0,0 |
| 22 | 0,2 | -од | 0,0 | 0,2* |
| 23 | 0,6* | -0,2 | -0,2 | -0,1 |
| 24 | 0,0 | 0,3* | -0,1 | 0,1 |
| 25 | -0,2 | ОД | 0,2* | 0,1 |
| 26 | -0,4 | 0,0 | 0,3* | |
| 27 | -0,1 | -0,3 | -0,1 | 0,5* |
| 28 | -0,4 | -0,1 | 0,5* | -0,2 |
| 29 | -0,2 | 0,2* | 0,2 | 0,0 |
| 30 | 0,6* | -0,2 | -0,3 | -0,2 |
| 31 | 0,0 | 0,0 | -0,1* | 0,3 |
| 32 | -0,1 | -0,1 | -0,1 | 0,4* |
| 33 | -0,3 | 0,6* | -0,1 | -0,2 |
| 34 | 0,3* | 0,0 | 0,0 | -0,1 |
| 35 | -0,2 | -0,1* | 0,1 | 0,3 |
| 36 | -0,1 | 0,5* | -0,2 | -0,1 |
| 37 | 0,2 | -0,2 | 0,0 | 0,2* |
| 38 | 0,1 | -0,1 | -0,1 | 0,3* |
| 39 | 0,5* | -0,3 | 0,0 | -0,3 |
Окончание табл. 5.24
| Задание | 1-й ответ | 2-й ответ | 3-й ответ | 4-й ответ |
| 40 | 0,2 | 0,2* | -0,4 | -0,2 |
| 41 | 0,3* | 0,0. | 0,1 | -0,1 |
| 42 | 0,1 | -0,1 | -0,1 | 0,4* |
теста. Второй столбец указывает на число испытуемых, выполнявших каждое из заданий первого столбца, все последующие столбцы содержат число и процент испытуемых, выбравших каждый из ответов к заданиям теста. Звездочкой отмечен процент, соответствующий правильному ответу к заданиям.
Анализ первой строки позволяет собрать полезную информацию о качестве задания 1 теста. В нем правильным является 3-й ответ, и поэтому число Р1 = 67% в столбце, соответствующем 3-му ответу, указывает на трудность задания 1 теста. Из 96 испытуемых, выполнивших задание, 65 справились с ним успешно, а остальные (96 - 65= 31) распределились между дистракторами к заданию 1 теста. Среди неправильно выполнивших это задание 8 тестируемых выбрали 1-й дистрактор, один тестируемый выбрал 2-й дистрактор и 22 испытуемых остановились при выполнении задания на 4-м, неправильном ответе.
Проведенный анализ позволяет сделать выводы о качестве разработанных дистракторов к заданию 1 с точки зрения их привлекательности для незнающих учеников.
Очень похож на правильный 4-й ответ: его выбрали 22 из 31 ученика. Второй ответ, выполняющий функцию дистрактора, явно непривлекательный: его выбрал всего один ученик, и потому этот ответ как неработающий дистрактор подлежит изменению либо удалению из теста.
Несомненно, нуждаются в переработке 1-й и 4-й ответы из задания 6, поскольку их не выбрал ни один человек из шести (97 — 91 = = 6), неправильно выполнивших это задание теста. Оба дистрактора ничего не дают для задания. Они просто создают иллюзию существования задания с четырьмя ответами. Необходимо также изменить 4-й ответ в задании 26, 2-й ответ в 38 и т.д.
Таким образом, в хороших заданиях с выбором ответов неверно ответившие ученики должны распределяться почти равномерно между всеми предложенными дистракторами. Дистракторы, которые выбирают менее 5% неверно ответивших испытуемых, должны быть удалены из теста.
Углубленный вариант дистракторного анализа построен на подсчете значения точечно-бисериального коэффициента корреляции для каждого дистрактора в заданиях теста. Формула для подсчета значений коэффициента и методика расчета приведены в разд. 5.2 (5.10). Отрицательные значения коэффициента корреляции указывают на ситуацию, когда хорошо выполнившие тест испытуемые не будут выбирать данный дистрактор в качестве правильного ответа.
Значения коэффициента точечно-бисериальной корреляции для примера из табл. 5.23 приводятся в табл. 5.24 (звездочка соответствует правильному ответу).
Выделенные положительные значения коэффициента точечно-бисериальной корреляции для дистракторов (например 2-й ответ в задании 4, 2-й ответ в задании 8, 4-й в 13 и т. д.) указывают на то, что эти неверные ответы выбирают в качестве правильных сильные ученики, что явно противоречит представлению преподавателя о хороших заданиях теста. Поэтому подобные задания, несомненно, следует проанализировать, и, если просчет в содержании не поддается коррекции, то просто удалить из теста. При правильном положении вещей значения коэффициента точечно-бисериальной корреляции для дистракторов должны быть отрицательными и превышающими по модулю 0,2. Положительные или близкие к нулю значения коэффициента для дистракторов говорят о необходимости их исключения либо переделки неправильных ответов.
В отличие от дистракторов в хороших заданиях правильные ответы выбираются сильными учениками. Поэтому значения коэффициента точечно-бисериальной корреляции на месте ответов со звездочкой не могут быть отрицательными. Правильным ответам должны соответствовать значения коэффициента корреляции, превышающие 0,5. Для случая, когда правильный ответ не выбирают сильные ученики (например в задании 31 или в заданиях 17, 35 из табл. 5.24), коэффициент корреляции бывает близким к нулю или даже меньше нуля. Отрицательная или нулевая корреляция для верного ответа может отражать случайный характер ответов учеников, наличие систематических проблем в усвоении проверяемого материала, вызванных дефектами преподавания либо некорректную формулировку задания теста.






