Метод расщепления на две части (split-half method) наиболее распространен из-за своего удобства. Он позволяет вычислить коэффициент надежности при однократном выполнении учениками теста. Для оценки надежности результаты тестирования делят на две части: в одну включают данные испытуемых по четным, а в другую — по нечетным заданиям теста. Правда, деление на две части — не единственный способ, возможны и другие варианты, когда выделяют большее число частей при оценке надежности теста.
Результаты учеников заносят в табл. 5.31 и получают табл. 5.32.
Далее для таблицы данных используют формулу (5.74), в которой роль результатов в первом тестировании выполняют данные по четным заданиям, а во втором — по нечетным.
Таблица 5.31. Сводная таблица для оценки надежности (метод расщепления)
| Номер ученика» | Балл при первом тестировании X, | Балл при втором тестировании Y, | XiYi | (Xi)2 | (Yi)2 |
| 1 | X1 | Y1 | X1Y1 | (X1)2 | (Y1)2 |
| 2 | X2 | Y2 | X2Y2 | (X2)2 | (Y2)2 |
| N | Xn | Yn | XnYn | (Xn)2 | (Yn)2 |
| СУММА (Xi) | СУММА (Yi) | СУММА(XiYi) | СУММА (Xi)2 | СУММА (Yi)2 |
Для матрицы табл. 5.28 результаты по четным и нечетным заданиям приводятся в табл. 5.32.
После подстановки чисел из табл. 5.32 в формулу (5.74) получается
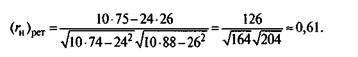
По сравнению с прежним значением 0,78 надежность получилась намного меньше, что можно было предвидеть, поскольку подсчет методом расщепления велся не по 10 заданиям, а только по 5. Для оценки надежности исходного теста из 10 заданий используется формула Спирмена—Брауна

Таблица 5.32. Подсчет надежности (метод расщепления)
| Номер ученика 1° | Балл при первом тес тировании X, | Балл при втором тес тировании Y, | Х,У, | (*У | (I? |
| 1 | 3 | 3 | 9 | 9 | 9 |
| 2 | 1 | 1 | 1 | 1 | 1 |
| 3 | 1 | 0 | 0 | 1 | 0 |
| 4 | 5 | 4 | 20 | 25 | 16 |
| 5 | 1 | 3 | 3 | 1 | 9 |
| 6 | 2 | 2 | 4 | 4 | 4 |
| 7 | 3 | 2 | 6 | 9 | 4 |
| 8 | 2 | 2 | 4 | 4 | 4 |
| 9 | 4 | 5 | 20 | 16 | 15 |
| 10 | 2 | 4 | 8 | 4 | 16 |
| Сумма | 24 | 26 | 75 | 74 | 88 |
Тогда rn теста из 10 заданий будет

После коррекции коэффициент надежности получился приблизительно такой же, как и в предыдущем случае подсчета ретестовым методом (гн =0,78). Применение формулы Спирмена— Брауна подтверждает высказанное ранее предположение: увеличение длины повышает надежность теста.
Рассмотренный выше метод расщепления основан на допущении параллельности двух половин теста, что не всегда и не в полной мере может оказаться верным. Корреляция двух половин возрастает по мере роста гомогенности теста. В этой связи метод расщепления нередко называют методом оценки внутренней состоятельности (согласованности) теста (Internal-Consistency Method).
Следующий подход к оценке надежности основан на вполне реальных данных и не зависит от упомянутых выше искусственных допущений о полной параллельности частей теста.
Однако и он имеет свою ограниченную сферу применения, поскольку годится исключительно для гомогенных тестов.
метол кьюаера— ричардсона (аля дихотомических ouehok по заданиям теста)
Формула Кьюдера— Ричардсона (F. Kuder, M. Richardson 20, или KR-20) имеет вид [48]
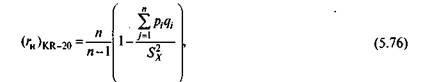
где р j — доля правильных ответов на j-е задание; qj — доля неправильных ответов, qj = 1 – pj, Sx 2 —дисперсия по распределению наблюдаемых баллов; п — число заданий теста.
Применительно к рассматриваемой матрице Sx 2 =6,89 (см.
разд. 5.2), a pj (j = 1,2,..., 10) приводится в самой последней строчке табл. 5.27. Тогда

Результат подсчета коэффициента надежности по формуле (5.76) довольно близок к двум другим полученным ранее (0,76 и 0,78).
Из обсуждения должно быть понятно, что не может быть какого-либо единственного показателя, доказывающего по оценке своих значений приемлемую надежность теста. Для полной ее проверки следует учитывать несколько показателей надежности, подсчитанных по разным формулам, лишь небольшая часть которых приведена в данном тексте.
В качестве нижнего предела допустимых значений надежности обычно выбирают 0,7. При более низком значении использование теста вряд ли целесообразно в силу большой погрешности измерения. Если тест разрабатывают профессионалы, то к нему предъявляют более жесткие требования. Как правило, тесты с надежностью менее 0,8 считаются непригодными в профессионально организованных службах тестирования и центрах. Значения коэффициента надежности, превышающие 0,9, говорят о высоком качестве теста. Они крайне желательны, но редко встречаются. Как правило, в тестологической практике надежность тестов колеблется в интервале (0,8; 0,9).
Положение с выводами о качестве теста осложняется тем, что нет и не может быть раз и навсегда определенной надежности теста. Ситуация вполне объяснимая, поскольку коэффициент надежности, подсчитываемый по матрице тестовых результатов, всегда зависит от свойств выборки испытуемых. Поэтому при каждом очередном использовании теста приходится оценивать его надежность, а уж потом говорить о достоверной интерпретации результатов выполнения теста.
В целом надежность зависит от ряда характеристик теста, рассмотрение которых может способствовать повышению качества теста в процессе его создания.
Надежность и длина теста
При конструировании теста полезно уметь определить необходимую его длину, чтобы достичь планируемой надежности теста. С этой целью используется обобщенный вариант формулы Спирмена—Брауна

где k — число раз, в которое увеличивается длина теста; rн — коэффициент надежности теста до увеличения его длины; (rн)' —коэффициент надежности после увеличения длины теста [12].
Конечно, увеличение длины в обсуждаемой постановке проблемы предполагается вести путем добавления заданий, содержание которых основано на той же спецификации, что и исходные задания теста. Таким образом, увеличение длины предполагает не изменение содержательной области, подвергающейся проверке, а детализацию проверки каждого содержательного элемента в тесте. Помимо этого, добавляемые задания должны иметь статистические характеристики, близкие к характеристикам исходных заданий теста. Нарушение одного из этих условий приводит, как правило, к неоправданному завышению оценок надежности теста.
Использование формулы (5.27) легко пояснить с помощью численных данных. Например, если надежность теста была rн=0,7идлину теста увеличили в 3 раза, то надежность нового теста возрастет до

что в отличие rн= 0,7 является вполне приемлемой для профессионального уровня создания теста.
Возможно другое применение формулы (5.77), когда достигнутая надежность, скажем rн=0,7, кажется разработчику явно недостаточной и он хочет узнать, во сколько раз следует увеличить длину для запланированного повышения качества теста. Если достигнутую надежность обозначить символом rдост, а планируемую, т.е. желательную — символом rплан, то

Для рассматриваемого выше примера, где rдост= 0,7, а rплан= 0,88,

Естественно, что надежность теста не является самоцелью, поскольку неоправданное увеличение длины теста, как уже было отмечено ранее, приведет к усталости и снижению мотивации у учеников, что в конечном счете отразится негативно на той же надежности теста. Поэтому при конструировании теста следует искать разумный компромисс, когда надежность теста находится в допустимых пределах, а длина теста выбрана сообразно возрастным особенностям учеников и специфике проверки. К тому же включение большого числа заданий, сходных по содержанию, нецелесообразно при итоговой проверке учеников.






