Рис. 5.5. Гистограмма эмпирического распределения
Для сравнения двух или более распределений обычно используют полигоны частот, так как при наложении гистограмм получается довольно запутанная картина. Например, с помощью полигонов можно сравнить результаты выполнения теста учащимися различных, в данном случае трех, классов, имеющих одинаковое количество учеников (рис. 5.6).
 Обозначения ——— 1-й класс
Обозначения ——— 1-й класс
...... 2-й класс
. _ _ _ 3-й класс
Наблюдаемые баллы
Рис. 5.6. Гистограмма эмпирического распределения
На рис. 5.6 отчетливо проглядывает значительное сходство в результатах тестирования у первых двух классов, имеющих довольно похожие полигоны распределения оценок.
Шестой шаг. На шестом шаге оцениваются меры центральной тенденции совокупности результатов, полученные при выполнении теста. Меры центральной тенденции предназначены для выявления «центрального положения», вокруг которого в основном группируется множество значений рассматриваемого распределения данных. Если предположить, что множество результатов расположено на прямой, то «центральное положение» имеет точка, вокруг которой по тому или иному признаку группируются все результаты выполнения теста. При анализе результатов тестирования можно использовать разные подходы к определению центра распределения. Наиболее простой способ основан на выявлении моды распределения.
Мода — это такое значение, которое встречается наиболее часто среди результатов выполнения теста. Например, для данных табл. 5.7 модой является балл 4, потому что он встречается чаще (3 раза) любого другого значения балла. Конечно, не всякое распределение имеет единственную моду. Например, в распределении баллов табл. 5.9есть две моды, одна из которых — 13, а другая — 19. По этой причине последнее распределение называется бимодальным. В том случае, когда все значения баллов учеников встречаются одинаково часто, принято считать, что моды у распределения нет.
Таблица 5.9. Бимодальное распределение баллов
| Балл | 10 | 11 | 13 | 15 | 16 | 19 | 21 | 22 |
| Частота | 2 | 3 | 5 | 4 | 2 | 5 | 2 | 1 |
Среднее выборочное (среднее арифметическое) определяется суммированием всех значений совокупности и последующим делением на их число. Для совокупности индивидуальных баллов Х1
Х2,..., XN группы N испытуемых среднее значение X будет

Среднее арифметическое индивидуальных баллов испытуемых для рассматриваемого выше примера матрицы (табл. 5.3 или 5.4) будет

Вычисление среднего значения легко произвести на любом калькуляторе или ПЭВМ. Процесс вычисления значительно упрощается, если отдельные значения в совокупности повторяются, как, например, в табл. 5.7. Для данных таблицы сумма всех результатов определяется умножением каждого значения балла на его частоту и последующим суммированием полученных произведений. Тогда среднее значение будет
В отличие от моды на величину среднего влияют значения всех результатов. Таким образом, среднее арифметическое характеризует всю совокупность значений. Оно обобщает индивидуальные особенности составляющих распределения, в нем уравниваются отдельные значения рассматриваемой величины. С другими свойствами среднего выборочного можно познакомиться в учебнике по статистике.
Вообще говоря, вычисление мер центральной тенденции — это механическая процедура, которую легко и быстро выполнит любая ПЭВМ. Однако получаемые результаты в процессе разработки теста требуют специальной интерпретации и размышления.
Интерпретация мер центральной тенденции. Меры центральной тенденции в определенной степени помогают при оценке качества теста в том случае, когда она проводится по результатам апробации теста на репрезентативной выборке учеников. Обычно считают, что хороший нормативно-ориентированный тест обеспечивает нормальное распределение индивидуальных баллов репрезентативной выборки учеников, когда среднее значение баллов находится в центре распределения, а остальные значения концентрируются вокруг среднего по нормальному закону, т.е. примерно 70% значений в центре, а остальные сходят на нет к краям распределения, как на рис. 5.7.

Рис. 5.7. Нормальная кривая распределения индивидуальных баллов
Если тест обеспечивает близкое к нормальному распределение баллов, то это означает, что на его основе можно определить устойчивое среднее значение баллов, которое принимается в качестве одной из репрезентативных норм выполнения теста. Обратный вывод, вообще говоря, неверен: устойчивость тестовых норм вовсе не предполагает обязательного нормального распределения эмпирических результатов выполнения теста.
У читателя может сложиться неправильное представление о том, что существует жесткая связь между нормальным распределением частот и практически любыми эмпирическими данными по тесту.
На самом деле это не так, поскольку нормальная кривая — это изобретение математиков, которое в сглаженном, идеальном виде описывает реальный полигон частот. На практике никогда не была и не будет получена совокупность данных, распределенных точно по нормальному закону. Просто иногда полезно, допуская определенную ошибку, утверждать, что эмпирические данные распределены по нормальному закону, и описывать полигон частот сглаженной кривой.
Нормальное распределение унимодально и симметрично, т.е. половина результатов, расположенная ниже моды, в точности совпадает с другой половиной, расположенной выше, а мода и среднее значение равны. Отсутствие полной симметрии в полигоне частот на практике приводит к смещению моды относительно среднего значения.
В малых выборках мода, как и среднее значение, теряет свою стабильность, хотя причиной нестабильности может служить и неправильный подбор по трудности заданий в тесте. Например, если по репрезентативной выборке получилась гистограмма с бимодальным распределением (рис. 5.8), то среднее значение распределения, находящееся в центре, никак не может служить нормой выполнения теста. Скорее всего, тест был сконструирован неудачно, что послужило причиной отсутствия нормального распределения эмпирических результатов выполнения теста.

3456789
Наблюдаемые баллы
Рис. 5.8. Гистограмма бимодального распределения
Смещение среднего значения влево или вправо, как на рис. 5.9 и 5.10, говорит о слишком трудной либо соответственно слишком легкой подборке заданий теста.
Таким образом, правильно сконструированный нормативно-ориентированный тест на репрезентативной выборке учеников

Наблюдаемые баллы
Рис. 5.9. Гистограмма распределения баллов по трудному тесту

Наблюдаемые баллы
Рис. 5.10. Гистограмма распределения баллов по легкому тесту
должен обеспечивать близкое к симметричному распределению индивидуальных баллов, когда мода и среднее значение примерно равны, а остальные результаты расположены вокруг среднего по нормальному закону.
Седьмой шаг. На седьмом шаге определяются описательные характеристики, служащие мерами изменчивости в группе данных по тесту. Введение характеристик связано с необходимостью выявления дополнительных оснований для обоснованного сравнения различных распределений по тестам. При сравнении нескольких распределений с одинаковыми средними с помощью дополнительных характеристик можно выявить существенные различия в структуре, указывающие на значительные отличия в качестве тестов.
Наиболее важная характеристика указывает на особенности разброса эмпирических данных вокруг среднего значения баллов по тесту. Отдельные значения индивидуальных баллов могут быть тесно сгруппированы вокруг своего среднего балла либо, наоборот,
сильно удалены от него. Поэтому необходимы оценки характеристик распределения, отражающие вариацию, или, как говорят иначе, изменчивость баллов по тесту.
Для характеристик степени рассеяния отдельных значений вокруг среднего используются различные меры: размах, дисперсия, стандартное отклонение.
Размах измеряет на шкале расстояние, в пределах которого изменяются все значения показателя в распределении. Например, распределения индивидуальных баллов табл. 5.6 размах равен 9 --1 = 8.
Вариационный размах легко вычисляется, но используется крайне редко при характеристике распределения баллов по тесту. И для этого есть веские основания. Во-первых, размах является весьма приближенным показателем, так как не зависит от степени изменчивости промежуточных значений, расположенных между крайними значениями в распределении баллов по тесту. Во-вторых, крайние значения индивидуальных баллов, как правило, ненадежны, поскольку содержат в себе значительную ошибку измерения. В этой связи более удачной мерой считается дисперсия.
Дисперсия. Подсчет дисперсии основан на вычислении отклонений каждого значения показателя от среднего арифметического в распределении. Для индивидуальных баллов значения отклонений
Xj - X (/=1,2,..., N) несут информацию о вариации совокупности
значений баллов Мучеников, т. е. отражают меру неоднородности результатов по тесту. Совокупность с большей неоднородностью будет иметь большие по модулю отклонения, наоборот, для однородных распределений отклонения должны быть близки к нулю. Знак отклонения указывает место результата ученика по отношению к среднему арифметическому по тесту. Для ученика с индивидуальным баллом выше среднего значение разности Xt - X будет положительно, а для тех, у кого результат ниже X, отклонение Xt - X меньше нуля.
Например, в распределении баллов со средним значением X = 5 из табл. 5.6 отклонения будут:
• для3-гоученика d 3 - Xl - X = l -5 = -4;
• для2-го d 2 = X 2 - X = 2-5 = ^-3;
• для 5-, 6- и 8-го d 5 6 8 =4-5 = -1;
для 7-го d 7 =5-5-0;
• для 1- и 10-го d, 10 =6-5 = 1;
• для 4- и 9-го fi?4i9=9-5 = 4.
Если просуммировать все отклонения, взятые со своим знаком, то для симметричных распределений сумма будет равна нулю. В рассматриваемом примере сумма отклонений
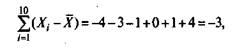
что, конечно, не позволяет оценить меру неоднородности распределения, поскольку отрицательные и положительные слагаемые уничтожают друг друга. Для преодоления этого эффекта каждое отклонение возводят в квадрат и находят сумму квадратов отклонений: Тогда сумма вида

будет большой, если результаты тестирования отличаются существенной неоднородностью, и малой — в случае близких результатов испытуемых по тесту.
Для рассматриваемого примера

Величина суммы зависит также от размера выборки учеников, выполнявших тест. Зависимость здесь вполне очевидна: чем больше учеников, тем больше положительных слагаемых в сумме, характеризующей вариацию баллов по тесту. Поэтому при сравнении мер изменчивости распределений, отличающихся по объему, возникает препятствие, которое снимается путем деления каждой суммы на N — 1, где N — число учеников, выполнявших тест. Определяемая таким образом мера изменчивости называется дисперсией. Она
обычно обозначается символом SI и вычисляется по формуле

Для рассматриваемого примера

В примере Sx вычислялась просто в силу того, что среднее арифметическое было целым числом. На практике, как правило, приходится иметь дело с дробными значениями X, что делает использование формулы (5.2) крайне утомительным. Поэтому нередко для подсчета дисперсии применяются другие формулы, приведенные в приложении 5.3.
Стандартное отклонение. Кроме дисперсии, для характеристики меры изменчивости распределения удобно использовать еще один показатель вариации, который называется стандартным отклонением. Стандартное отклонение равно корню квадратному из дисперсии:
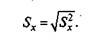
Для рассматриваемого примера

Свойства дисперсии и стандартного отклонения рассматриваются подробно в учебниках по статистике. Заинтересованному читателю можно порекомендовать, например, книгу Дж. Гласе, Дж. Стенли «Статистические методы в педагогике и психологии» [9].
Стандартное отклонение не следует путать со средним отклонением, последнее находится по формуле

и является средним значением суммы отклонений, взятых по модулю.
Интерпретация. Дисперсия играет важную роль в оценке качества нормативно-ориентированных тестов. Слабая вариация результатов испытуемых указывает на низкое качество теста. Основания для подобного вывода вполне прозрачны. Низкая дисперсия индивидуальных баллов говорит о слабой дифференциации испытуемых по уровню подготовки в тестируемой группе, т.е. о той ситуации, которая диаметрально противоположна основной цели создания нормативно-ориентированного теста.
Излишне высокая дисперсия, характерная для случая, когда все учащиеся отличаются по числу выполненных заданий, также грозит неприятными последствиями и требует переработки теста. Превышение разумных пределов величины дисперсии приводит к искажению вида распределения, которое начинает существенно отличаться от планируемой теоретической нормальной кривой.
При переработке теста следует руководствоваться простым правилом: если проверка согласованности эмпирического распределения с нормальным дает положительные результаты, а дисперсия растет, то это означает, что происходит повышение дифференцирующей способности теста и процесс улучшения теста.
Конечно, использовать какой-либо из существующих критериев для проверки нормальности распределения в практике довольно неудобно. Поэтому зачастую непрофессионалы в оценке характера распределения руководствуются простым соотношением. Для
этого величину X сравнивают с утроенным стандартным отклонением. Если это равенство выполняется, т.е. если

то дисперсия оптимально высока и можно принять гипотезу о нормальности распределения.
Стандартное отклонение является крайне полезной мерой вариации для случая нормального распределения баллов испытуемых, так как заранее приблизительно известно, какой процент данных лежит внутри одного, двух и трех стандартных отклонений, откладываемых от центра распределения. Наиболее удобна нормированная нормальная кривая, площадь под которой равна 1 (рис. 5.1 1).
Для нее среднее значение z =0, а стандартное отклонение аг=1.
Для совмещения любой нормальной кривой с единичной достаточно выполнить простое преобразование исходного распределения путем вычитания среднего значения X из каждого индивидуального балла X, и деления полученной разности на Sx (подробнее см. гл. 7):
- 99.72%

Рис. 5.11. Нормальное распределение для z =0 и a г = 1
Вообще существует бесконечное множество нормальных кривых, отличающихся друг от друга значениями X и Sx, но все они объединяются общими свойствами, которые связаны с долями площади под кривой, в пределах определенного числа отклонений. А именно, в любом нормальном распределении приблизительно:
1) 68% площади под кривой лежит в пределах одного стандартного отклонения, откладываемого влево и вправо от среднего (т.е. (X ±1 SX),
2) 95% площади под кривой лежит в пределах двух Sx, откладываемых слева и справа от среднего (X ±2 SX),
3) 99,7% площади под кривой лежит в пределах трех 5^ влево и
вправо от X (X ±3 SX).
Что касается нормативно-ориентированного теста, то при его разработке необходимо помнить о том, что кривая распределения индивидуальных баллов, получаемых на репрезентативной выборке, является следствием кривой распределения трудности заданий теста. Этот факт удачно иллюстрируется рис. 5.12.
Для первого распределения слева характерно явное смещение в тесте в сторону легких заданий, что, несомненно, приведет к появлению большого числа завышенных баллов у репрезентативной выборки учеников. Большая часть учеников выполнит почти все задания теста.
Второй случай (слева) отражает существенное смещение в сторону трудных заданий при разработке теста, что не может не сказаться на снижении результатов учеников, поэтому распределение индивидуальных баллов имеет явно выраженный всплеск вблизи начала горизонтальной оси. Основная часть учеников выполнит незначительное число наиболее легких заданий теста.
В третьем случае задания теста обладают оптимальной трудностью, поскольку распределение имеет вид нормальной кривой. Отсюда автоматически возникает нормальность распределения. индивидуальных баллов репрезентативной выборки учеников, что в свою очередь позволяет считать полученное распределение устойчивым по отношению к генеральной совокупности. Следовательно, именно в третьем случае можно определить репрезентативные нормы выполнения теста.

Рис. 5.12. Связь распределения индивидуальных баллов и трудности
Заданий теста
Таким образом, возникает нетривиальный вывод для тех, кто привык к традиционным контрольным работам, когда результаты по классу считаются вполне достоверными и хорошими, если контрольную работу выполняет основная масса учеников. В тесте все обстоит несколько иначе. Если нормального распределения нет, то нет никакого основания доверять полученным результатам учеников. Поэтому в профессионально разработанных нормативно-ориентированных тестах типичным является результат, когда приблизительно 70% учеников выполняют правильно от 30 до 70% заданий теста, а наиболее часто встречается результат в 50%.
Восьмой шаг. На следующем шаге оцениваются меры симметрии и островершинности кривых распределений.
Асимметрия. Степень отклонения распределения наблюдаемых частот выборки от симметричного распределения, характерного для нормальной кривой, оценивается с помощью асимметрии. Наличие асимметрии легко установить визуально, анализируя полигон частот или гистограмму. Более тщательный анализ можно провести с помощью обобщенных статистических характеристик, предназначенных для оценки асимметрии в распределении.
На рис. 5.13 представлены кривые распределения с отрицательной, нулевой и положительной асимметрией (слева направо) соответственно

Наиболее удачная формула для подсчета асимметрии имеет вид

где Xt —• индивидуальный балл/-го ученика; X — среднее значение баллов по тестируемой группе;  — куб стандартного отклонения; N — число учеников. После подстановки данных из рассматриваемого выше примера (табл. 5.3) величина асимметрии будет равна
— куб стандартного отклонения; N — число учеников. После подстановки данных из рассматриваемого выше примера (табл. 5.3) величина асимметрии будет равна

Интерпретация. При интерпретации полученного значения асимметриии 0,2 необходимо обратить внимание на то, что вклад положительных значений кубов разностей Xi - X будет больше кубов отрицательных значений, но ненамного, поэтому величина асимметрии получилась положительной и небольшой. Таким образом, асимметрия распределения положительна, если основная часть значений индивидуальных баллов лежит справа от среднего значения, что обычно характерно для излишне легких тестов. Асимметрия распределения баллов отрицательна, если большинство учеников получили оценки ниже среднего балла. Эффект отрицательной асимметрии встречается в излишне трудных тестах, не сбалансированных правильно по трудности при отборе заданий в тест.
В хорошо сбалансированном по трудности тесте, как уже отмечалось ранее, распределение баллов имеет вид нормальной кривой. Для нормального распределения характерна нулевая асимметрия, что вполне естественно, так как при полной симметрии каждое значение балла, меньшее X, уравновешивается другим симметричным, большим, чем X.
Эксцесс. С помощью эксцесса можно получить представление о том, являются ли полигон частот или гистограмма островершинными или плоский. На рис. 5.14 изображены три кривые, отличающиеся по эксцессу.

Первая кривая (А) — островершинная, имеет явно выраженный положительный эксцесс, вторая кривая (В) — средне вершинная, имеет нулевой эксцесс, характерный для нормальной кривой, третья кривая (С) — плосковершинная, кривые такого типа имеют эксцесс меньше нуля.
Обычно эксцесс вычисляется по формуле

где все обозначения остались прежними. Для рассматриваемого примера (см. табл. 5.6) эксцесс будет

Интерпретация. При интерпретации полученных оценок эксцесса необходимо помнить о том, что понятие «эксцесс» применимо лишь к унимодальным распределениям. Более того, интерпретация результата, указывающего на крутизну кривой распределения, возможна в сравнительно небольшой окрестности моды и теряет свой смысл по мере удаления вдоль кривой.
В том случае, когда распределение данных бимодально (имеет две моды), необходимо говорить об эксцессе в окрестности каждой моды. Бимодальная конфигурация указывает на то, что по результатам выполнения теста выборка учеников разделилась на две группы. Одна группа справилась с большинством легких, а другая с большинством трудных заданий теста. Один из наиболее важных выводов в случае бимодального распределения нацелен на коррекцию трудности заданий теста. По-видимому, в тесте недостаточно представлены задания средней трудности, позволяющие выровнять распределение баллов, приблизив его к нормальной кривой.
В заключение необходимо провести проверку значимости найденных значений асимметрии и эксцесса. Для этого необходимо добавить информацию о принимаемом уровне риска допустить ошибку в статистическом выводе. Наиболее приемлемым для педагогических измерений является уровень в 5%, который допускает ошибку в пяти случаях из ста. После выбора степени риска проверка значимости проводится одним из описанных в литературе методов [36].
Девятый шаг. Девятый шаг предназначен для вычисления показателей связи между результатами учеников по отдельным заданиям теста. При оценке качества заданий важно понять, существует ли тенденция, когда одни и те же ученики добиваются успеха в какой-либо паре заданий теста. Либо, наоборот, такой тенденции, указывающей на связь результатов, нет, и состав учеников, добивающихся успеха, полностью меняется при переходе от одного задания к другому в тесте.
Очевидно, для ответа на поставленные вопросы необходимо провести анализ данных, собрав их в таблицу. Однако такой визуальный анализ данных — дело достаточно утомительное, а для больших выборок и просто невозможное. Поэтому обычно ответ на вопрос о существовании связи между двумя наборами данных получают с помощью корреляции.
Корреляция. Корреляция в широком смысле слова означает связь между явлениями и процессами, Однако для исследования связи установить ее наличие недостаточно, необходимо также правильно выбрать ее вид и форму показателя, предназначенного для оценки меры связи между явлениями.
Связь между двумя наборами данных Х и У можно выразить графически с помощью диаграммы рассеяния (рис. 5.15).

Рис. 5.15. Диаграмма рассеяния, показывающая связь результатов
тестирования группы школьников по математике (X) с результатами






