Усовершенствованный метод Эйлера

Характерной особенностью метода является использование в качестве направления поиска каждой последующей точки численного решения касательной, определяемой в центре отрезка [ x_k, x_k ₊₁]. Как видно на рис.4 для k = 0, последовательно выполняются два шага по методу Эйлера.

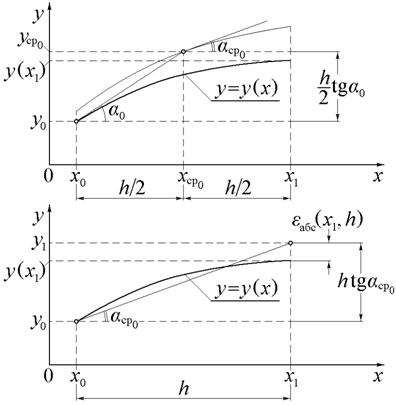Первый из них используется для вычисления тангенса угла наклона касательной в средней точке отрезка [ x_k, x_k ₊₁]

После этого делается второй шаг – для вычисления новой точки

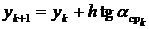Если тангенсы углов наклона касательных заменить на правую часть дифференциального уравнения f (x, y), то вышеприведенные формулы для выполнения одного шага по усовершенствованному методу Эйлера сведутся к следующим

, ,

, .

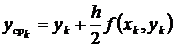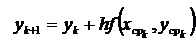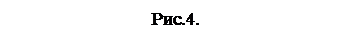Этот метод является методом второго порядка точности. Он даёт меньшую погрешность численного решения на шаге h, чем метод Эйлера. Его абсолютная погрешность ε _абс(x_k ₊₁, h) на каждом шаге пропорциональна величине h ³, а решение совпадает с истинным в случае, когда оно представимо квадратичной функцией y = a ₁+ a ₂ x + a ₃ x ². Однако это достигается тем, что его трудоемкость увеличивается примерно в два раза, поскольку для одного шага приходится два раза вычислять значение правой части дифференциального уравнения.

Метод Рунге–Кутта (C.Runge 1895, W.Kutta 1901)

Под наименованием «метод Рунге–Кутта» принято подразумевать целое семейство методов численного решения задачи Коши, объединенных одной идеей выбора некоторого усреднённого направления поиска каждой новой точки приближённого решения. Алгоритм одного из этих методов: метода Рунге–Кутта 4-го порядка, строится по следующей схеме. Из начальной точки, как это можно видеть на рис.5 для k = 0, в направлении касательной делается шаг по методу Эйлера на величину h/ 2 и в полученной точке вычисляется тангенс угла наклона касательной

, ,

Из начальной точки по найденному направлению делается второй шаг на ту же величину и определяется тангенс угла наклона во второй средней точке

Третий шаг делается опять из начальной точки по последнему найденному направлению (), но на шаг h, где опять находится тангенс угла наклона касательной

Последний шаг из начальной точки на величину h делается по присущему этому методу осреднённому направлению и находится ордината следующей точки приближённого решения

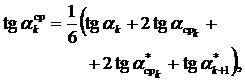
Описанные действия, необходимые для получения координат каждой последующей точки приближённого решения, реализуются в виде следующей последовательности вычислений по формулам

, ,

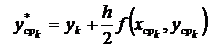Получающееся численное решение имеет на каждом шаге h погрешность ε _абс(x_k ₊₁, h), которая пропорциональнавеличине h ⁵. Оно совпадает с истинным в случае, когда оно – многочлен четвёртого порядка y = a ₁+ a ₂ x + a ₃ x ²+ a ₄ x ³+ a ₅ x ⁴.

Оценка погрешностей методов

Как уже отмечалось выше, при использовании метода Эйлера на каждом шаге положение следующей точки решения, вычисляется с использованием информации о правой части f (x, y) уравнения только в крайней левой точке отрезка [ x_k, x_k ₊₁]. В результате его абсолютная погрешность на каждом шаге пропорциональна величине h ²

где

В формуле для C_k ₊₁ в качестве функции y используется некая промежуточная функция, график которой располагается между графиками приближённого и неизвестного точного решений.

Аналогичные соотношения для оценки абсолютных погрешностей на каждом шаге можно привести для усовершенствованного метода Эйлера

где

и метода Рунге–Кутта 4-го порядка

где формула для C_k ₊₁ не приводится из-за своей громоздкости.

Так как на отрезке интегрирования дифференциального уравнения требуется выполнить несколько шагов, то общая абсолютная погрешность вычисления приближённого решения в точке x_n будет складываться из погрешностей каждого отдельного шага

где m = 2 для метода Эйлера, m = 3 для усовершенствованного метода Эйлера и m = 5 для метода Рунге–Кутта 4-го порядка, а параметры C _max и q определяются следующим образом

, .

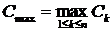Приведённое соотношение для абсолютной погрешности имеет одно важное свойство. Знак параметра q определяет характер изменения её величины, накапливаемой в процессе пошагового решения задачи Коши. Положительные значения q обуславливают лавинообразное накопление погрешности, а отрицательные – указывают на тенденцию её уменьшения.

Такое вычисление абсолютных погрешностей решения задачи Коши затруднено, так как требует решения дополнительной, зачастую даже более сложной, задачи поиска максимума высших производных правой части уравнения. Поэтому чаще для вычисления погрешности методов используют апостериорные оценки, базирующиеся на правиле Рунге (правило двойного счёта), идея которого описана в лабораторной работе №1. Его основное соотношение, справедливое для всех способов приближённого решения задачи Коши, имеет вид

где y (x_k, h) и y (x_k, 2 h) – приближённые значения решения, вычисленные в точке x_k при шагах интегрирования, отличающихся друг от друга в два раза.

В качестве относительной погрешности решения задачи Коши на отрезке [ x ₀, x_n ] его построения, часто используют её интервальную оценку, равную отношению абсолютной погрешности к максимальному значению модуля решения на данном отрезке

Работа методов и оценка погрешности получаемых результатов может быть проиллюстрирована на примере построения приближённого решения задачи Коши для уравнения с начальным условием y (0) = 0 на отрезке [0, 0.4] с шагом h = 0.1.

1. Решение задачи методом Эйлера. В соответствии с алгоритмом метода расчётная схема может быть представлена в виде следующих соотношений

Таким образом, пошаговый процесс построения решения с заданным шагом интегрирования h = 0.1 будет выглядеть следующим образом

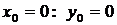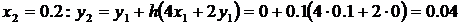Для оценки погрешности полученного решения необходимо повторить проделанные расчёты с удвоенным шагом интегрирования h = 0.2

Полученные результаты позволяют оценить абсолютную и относительную погрешности решения с шагом интегрирования h = 0.1

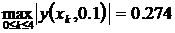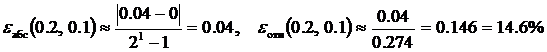2. Решение задачи усовершенствованным методом Эйлера. В данном случае расчётная схема метода представляется в виде соотношений

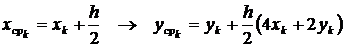
В соответствии с этим процесс построения решения с шагом интегрирования h = 0.1 будет иметь вид

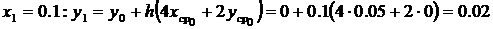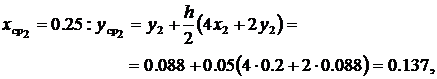
Аналогично предыдущему примеру, где реализован метод Эйлера, для вычисления погрешности решения с шагом h = 0.1 повторяются расчёты с шагом h = 0.2

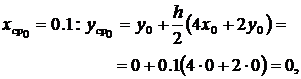
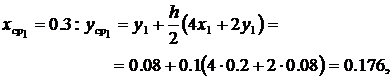
Откуда абсолютная и относительная погрешности решения с шагом h = 0.1 будут соответственно равны

Программное обеспечение. В качестве исходного материала для выполнения заданий лабораторной работы предложены относительно простые тексты программ, реализующих следующие методы:

- метод Эйлера Subroutine Eu_1(d,m,F,x,y);

- усовершенствованный метод Эйлера

Subroutine EuY_1(d,m,F,x,y);

- метод Рунге-Кутта 4-го порядка Subroutine RK4_1(d,m,F,x,y).

В качестве параметров в подпрограммах используются:

d - длина отрезка интегрирования дифференциального уравнения первого порядка (Real*4);

m - количество шагов на отрезке интегрирования (Integer*4), шаг h интегрирования уравнения определяется как частное от деления длины отрезка d на количество шагов m на нём;

F - имя внешней подпрограммы типа Function, с помощью которой вычисляются значения правой части f (x, y) уравнения;

x - значение аргумента дифференциального уравнения в начале отрезка интегрирования при обращении к подпрограммам и в конце этого отрезка (x + d) после их отработки (Real*4);

y - значение функции y (x) – приближённого решения дифференциального уравнения (Real*4).

Имя подпрограммы F должно быть объявлено как External в программном модуле, который обращается к данным подпрограммам, а сама подпрограмма оформляется в виде

Function F(x,y)

F =...........

Return

End

Пример выполнения задания. Получить решение задачи Коши на указанном отрезке

, , .

с использованием метода Эйлера. Подобрать величину шага интегрирования так, чтобы относительная погрешность решения не превышала 1%.

Решение. В приведенной ниже программе численное решение задачи Коши выполняется подпрограммой Eu_1, реализующей метод Эйлера, правая часть уравнения – описывается в подпрограмме Fun типа Function, а начальное условие – задаётся явно в тексте основной программы. Если в результате решения задачи максимальное значение относительной погрешности будет превышать 1%, то вычисления должны быть выполнены ещё раз с меньшими значениями шага интегрирования.

External Fun

Real*4 Xm(51), Ys(51), Yn(51), Eps(51)

Open(6, file='res_6.txt')

c Расчёт с шагом h=0.1

x = 0.

y = 0.

Xm(1) = x

Ys(1) = y

Do k = 2, 51

Call Eu_1(0.1, 1, Fun, x, y)

Xm(k) = x

Ys(k) = y

EndDo

c Расчёт с шагом h=0.05

x = 0.

y = 0.

Yn(1) = y

Do k = 2, 51

Call Eu_1(0.1, 2, Fun, x, y)

Yn(k) = y

EndDo

c Оценка погрешности решения с шагом h=0.05

Ymax = 0

Do k = 1, 51

If(Abs(Yn(k)).gt.Ymax) then

Ymax = Abs(Yn(k))

Endif

EndDo

Do k = 1, 51

Eps(k) = Abs(Ys(k) - Yn(k))/Ymax

EndDo

Write(6,2) (Xm(k), Yn(k), Eps(k), k = 1, 51)

2 Format(2X, 'x=', F4.1, ' y=', F6.4, ' e=', F6.4)

Call Graf_1(51, Xm, Yn, 'x', 'y', ' ', 1)

Close(6)

End

Function Fun(x, y)

Pi = 3.1415927

Fun = 1 + Exp(-x)*Cos(Pi*x) - y

Return

End

В процессе выполнения программы осуществляется пошаговая печать в файл rеs_6.txt. В результате он будет заполнен следующей информацией

x=.0 y=.0000 e=.0000

x=.1 y=.1920 e=.0081

x=.2 y=.3500 e=.0162

x=.3 y=.4724 e=.0235

x=.4 y=.5605 e=.0293

x=.5 y=.6182 e=.0334

..........................

x= 5.0 y=.9944 e=.0011

Анализ результатов показывает, что максимальное значение относительной погрешности равно 3.59% при x = 0.7 и значительно превышает требуемую величину. Поэтому расчёты должны быть повторены при меньшем значении шага интегрирования. Последующие расчёты с различными значениями шага показали, что заданная погрешность решения достигается только при шаге h = 0.0125.

График численного решения рассматриваемой задачи Коши, полученный на экране монитора, представлен на рис.6.

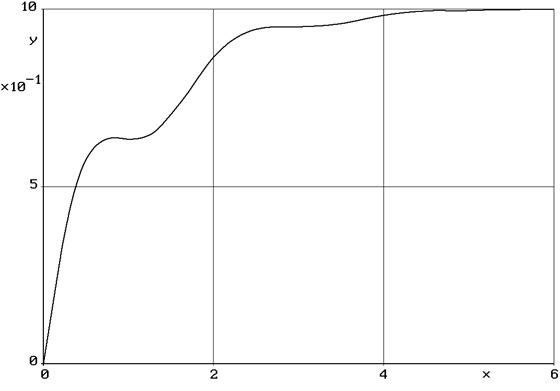
Рис.6.

Глава 7. РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ НОРМАЛЬНЫХ СИСТЕМ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ УРАВНЕНИЙ ВЫСШИХ ПОРЯДКОВ

Задача Коши для нормальной системы обыкновенных дифференциальных уравнений записывается в виде

или в матричной форме

, ,

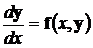где

, , .

Система дифференциальных уравнений связывает независимую переменную x, искомые функции y ₁, y ₂, ..., y _n и их первые производные. В данном случае решение задачи Коши заключается в отыскании функций y ₁= y ₁(x), y ₂= y ₂(x),..., y _n = y _n (x), обращающих каждое уравнение системы в тождество на конечном или бесконечном интервале (a, b) и удовлетворяющих начальным условиям.

Такая форма записи задачи Коши является канонической для систем обыкновенных дифференциальных уравнений. К ней могут быть приведены как любые другие формы представления систем дифференциальных уравнений, разрешённых относительно старших производных, так и дифференциальные уравнения высших порядков. Приведение дифференциальных уравнений высших порядков к нормальной системе дифференциальных уравнений осуществляется по следующей схеме. Если дана задача Коши следующего вида

, , , …, ,

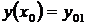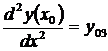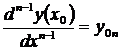то замена переменных

, , , …, ,

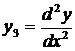сводит её к нормальной системе дифференциальных уравнений с начальными условиями

, ,

образующих задачу Коши.

Для решения такой задачи Коши используются те же методы, что для обыкновенных дифференциальных уравнений 1-го порядка. Это обуславливается тем, что матричная форма записи задачи Коши для нормальной системы полностью совпадает с её формулировкой для этих уравнений. Аналогична для неё и теорема о существовании единственного решения. Единственным отличием здесь является то, что вместо функций y (x) и f (x, y) используются вектор-функции y и f, состоящие из n функций y ₁(x), y ₂(x),..., y _n (x) и f ₁(x, y ₁,..., y _n), f ₂(x, y ₁,..., y _n),..., f _n (x, y ₁,..., y _n), соответственно. При этом расчётные схемы методов и оценки их погрешностей сохраняются.

Метод Эйлера

Соотношения метода Эйлера для нормальной системы в матричной форме имеют вид

или в развернутой форме

, ,

где верхний индекс показывает номер шага по аргументу x.

Геометрическая интерпретация работы метода Эйлера решения задачи Коши для нормальной системы идентична его геометрической интерпретации для дифференциальных уравнений 1-го порядка. Однако в данном случае движение осуществляется вдоль некоторой кривой в (n +1)-мерном пространстве переменных x, y ₁, y ₂,..., y _n, которая является геометрическим представлением вектор-функции y.

Усовершенствованный метод Эйлера

Основные соотношения усовершенствованного метода Эйлера в матричной форме записываются следующим образом

, ,

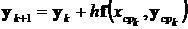что в развернутом виде даёт

, ,

, .

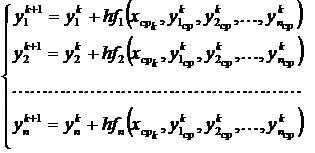Метод Рунге-Кутта

Преобразование соотношений метода Рунге-Кутта 4-го порядка точности на случай решения нормальной системы дифференциальных уравнений в матричной форме приводит к следующему

, ,

Как видно из приведенных формул, алгоритм метода строится по той же схеме из 4-х шагов, но в (n +1)-мерном пространстве. При этом направление отыскания следующей точки приближённого решения определяется вектором, каждая компонента которого вычисляется как некоторое осреднённое значение тангенса угла между касательной к интегральной гиперкривой и осью аргумента системы x.

В развернутом виде соотношения метода Рунге-Кутта для нормальной системы из n уравнений записываются в виде

, ,

Оценка погрешностей методов

Все оценки погрешности, полученные для решений задачи Коши для одного дифференциального уравнения 1-го порядка, остаются справедливыми и для решения систем аналогичных дифференциальных уравнений. В силу этого абсолютная погрешность метода Эйлера на каждом шаге пропорциональна величине h ²

Здесь

где

При вычислении коэффициента C_k ₊₁ в качестве вектор-функции y используется некая промежуточная функция, кривая которой в (n +1)-мерном пространстве переменных x, y ₁, y ₂,..., y _n, располагается между кривыми приближённого и неизвестного точного решений.

Абсолютная погрешность усовершенствованного метода Эйлера на каждом шаге пропорциональна величине h ³

где

а метода Рунге–Кутта 4-го порядка – h ⁵

где выражение для коэффициента C_k ₊₁ аналогично приведённым для методов Эйлера и не приводится из-за своей громоздкости.

Абсолютная погрешность вычисления приближённого решения на отрезке интегрирования системы дифференциальных уравнений складывается из погрешностей каждого отдельного шага. Поэтому общая погрешность решения после n -го шага оценивается следующим образом

где m = 2 для метода Эйлера, m = 3 для усовершенствованного метода Эйлера и m = 5 для метода Рунге–Кутта 4-го порядка и

, .

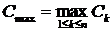Знак параметра q определяет характер изменения величины абсолютной погрешности решения задачи Коши. Его положительные значения приводят к накоплению погрешности при увеличении длины отрезка интегрирования, а отрицательные – к её уменьшению.

На практике такое вычисление абсолютных погрешностей решения задачи Коши затруднено. Поэтому, как правило, для вычисления погрешности методов используют апостериорную оценку, базирующуюся на правиле Рунге

где y (x_k, h) и y (x_k, 2 h) – приближённые значения вектора решения, вычисленные в точке x_k при шагах интегрирования, отличающихся друг от друга в два раза.

В качестве относительной погрешности решения задачи Коши на отрезке [ x ₀, x_n ] как и в случае одного дифференциального уравнения 1-го порядка используют интервальную оценку

Алгоритмы методов решения задачи Коши и оценка погрешности получаемых результатов могут быть проиллюстрированы на примере решения уравнения с начальными условиями y (0) = 0, на отрезке [0, 0.4] с шагом h = 0.1.

На первом этапе дифференциальное уравнение 2-го порядка должно быть преобразовано к эквивалентной системе дифференциальных уравнений 1-го порядка. Для этого вводятся следующие обозначения

что позволяет записать исходную задачу Коши в виде системы

, .

В соответствии с алгоритмом метода Эйлера расчётная схема решения системы дифференциальных уравнений может быть представлена в виде следующих соотношений

, .

Таким образом, процесс решения с заданным шагом интегрирования h = 0.1 будет выглядеть следующим образом

Для получения оценки погрешности решения необходимо повторить проделанные расчёты с удвоенным шагом h = 0.2

Эти результаты позволяют оценить абсолютную и относительную погрешности решения с шагом интегрирования h = 0.1

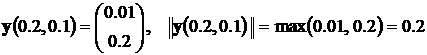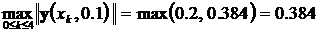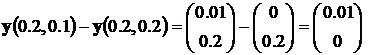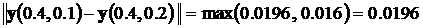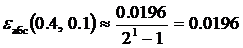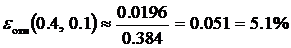Из этих расчётов видно, что решение рассматриваемой задачи Коши методом Эйлера с шагом 0.1 на отрезке [0, 0.4] получено с относительной погрешностью не большей, чем 5.1%.

Программное обеспечение. В математической библиотеке IMSL имеется подпрограмма решения систем обыкновенных дифференциальных уравнений 1-го порядка при помощи методов Рунге-Кутта-Вернера 5-го и 6-го порядка

Subroutine Ivprk(Ido,n,Fun,x,xd,Eps,Param,Y).

В качестве параметров в подпрограмме используются:

Ido - рабочий параметр подпрограммы, характеризующий стадию вычислений (Integer*4);

n - порядок системы обыкновенных дифференциальных уравнений (Integer*4);

Fun - имя внешней подпрограммы типа Subroutine, с помощью которой вычисляется вектор правых частей системы уравнений. Оно должно быть объявлено как External в программной единице, обращающейся к подпрограмме Ivprk. Подпрограмма Fun оформляется в виде

Subroutine Fun(n,x,Y,F)

Dimension Y(n), F(n)

F(1) =...........

..................

F(n) =...........

Return

End

Здесь F - массив значений вектора правой части f (x, y) системы уравнений (Real*4).

x - аргумент системы уравнений, который содержит его начальное значение (Real*4);

xd - конечное значение аргумента системы (Real*4);

Eps - абсолютная погрешность решения – подпрограмма автоматически регулирует величину шага интегрирования для обеспечения заданной величины погрешности (Real*4);

Param - массив из 50-ти элементов, содержащий необязательные параметры управления процессом вычислений. Его нулевое значение означает, что массив задан по умолчанию, см. [6] (Real*4);

Y - массив (n элементов) значений вектора решения y (x) системы уравнений (Real*4).

Параметр Ido задается равным 1 при первом обращении к подпрограмме для обеспечения автоматического выделения рабочей области памяти. В процессе работы подпрограммы его значение автоматически устанавливается равным 2, которое сохраняется при повторных вызовах подпрограммы.

При использовании подпрограммы Ivprk в циклических алгоритмах после завершения каждого цикла требуется освобождение рабочей области. Это достигается путём повторного вызова подпрограммы с параметром Ido=3. В прочих случаях подобная операция необязательна. О других возможных значениях этого параметра см. [8].

Для аргументов двойной точности (Real*8) используется подпрограмма с именем DIvprk.

В качестве исходного материала для выполнения заданий лабораторной работы предложены относительно простые тексты программ, реализующих следующие методы:

- метод Эйлера Subroutine Eu_n(n,d,m,Fun,x,Y);

- усовершенствованный метод Эйлера

Subroutine EuY_n(n,d,m,Fun,x,Y);

- метод Рунге-Кутта 4-го порядка

Subroutine Rk4_n(n,d,m,Fun,x,Y).

В качестве параметров в подпрограммах используются:

n - порядок решаемой системы обыкновенных дифференциальных уравнений (Integer*4);

d - длина отрезка интегрирования уравнений (Real*4);

m - количество шагов на отрезке интегрирования, выполняемых подпрограммой (Integer*4);

Fun - имя внешней подпрограммы типа Subroutine, с помощью которой вычисляются значения вектора правой части f (x, y) системы. Её вид приведён выше;

x - значение аргумента системы уравнений в начале отрезка интегрирования при обращении к подпрограммам и в конце этого отрезка (x + d) после их отработки (Real*4);

Y - массив (n элементов) значений вектора решения y (x) системы уравнений (Real*4).

Пример выполнения задания. Получить решение задачи Коши на указанном отрезке

с использованием метода Эйлера. При решении задачи подобрать такой шаг интегрирования, при котором относительная погрешность не превышала бы 0.1%.

Решение. Для численного решения исходной задачи Коши её необходимо преобразовать к эквивалентной нормальной системе дифференциальных уравнений. Это достигается путем введения следующего обозначения искомого решения задачи Коши и его производных

Такая замена позволяет свести исходную задачу Коши к системе обыкновенных дифференциальных уравнений 1-го порядка и новым начальным условиям

, .

Ниже приведён текст программы, позволяющей получить численное решение задачи Коши и оценку его относительной погрешности. Если в результате решения задачи максимальное значение относительной погрешности будет превышать 0.1%, то вычисления должны быть выполнены ещё раз с меньшими значениями шагов.

External Fun

Real*4 Xm(61),Y(4),Ys(4,61),Yn(4,61),EpsMax(4),

* Eps(61),Ym(61)

Open(6, file='res_7.txt')

c Расчёт с шагом h=0.1

x = 0.

Y(1) = 0.

Y(2) = 1.

Y(3) =-2.

Y(4) = 3.

Xm(1) = x

Do i = 1, 4

Ys(i,1) = Y(i)

Enddo

Do k = 2, 61

Call Eu_n(4, 0.1, 1, Fun, x, Y)

Xm(k) = x

Do i = 1, 4

Ys(i,k) = Y(i)

Enddo

EndDo

c Расчёт с шагом h=0.05

x = 0.

Y(1) = 0.

Y(2) = 1.

Y(3) =-2.

Y(4) = 3.

Do i = 1, 4

Yn(i,1) = Y(i)

Enddo

Do k = 2, 61

Call Eu_n(4, 0.1, 2, Fun, x, Y)

Do i = 1, 4

Yn(i,k) = Y(i)

Enddo

EndDo

c Оценка погрешности решения с шагом h=0.05

Ymax = 0

Do k = 1, 61

Do i = 1, 4

If(Abs(Yn(i,k)).gt.Ymax) Ymax = Abs(Yn(i,k))

Enddo

EndDo

Do k = 1, 61

Do i = 1, 4

EpsMax(i) = Abs(Ys(i,k) - Yn(i,k))/(3*Ymax)

Enddo

Eps(k) = EpsMax(1)

Do i = 2, 4

If(EpsMax(i).gt.Eps(k)) Eps(k) = EpsMax(i)

Enddo

Ym(k) = Yn(1,k)

EndDo

Write(6,2) (Xm(k), Ym(k), Eps(k), k = 1, 61)

2 Format(2X, 'x=', F4.1, ' y=', F6.4, ' e=', F7.5)

Call Graf_1(61, Xm, Ym, 'x', 'y', 'N', 1)

Close(6)

Stop

End

Subroutine Fun(n, x, Y, F)

Dimension Y(n), F(n)

F(1) = Y(2)

F(2) = Y(3)

F(3) = Y(4)

F(4) = 2*Y(3) - Y(1)

Return

End

В процессе выполнения программы осуществляется пошаговая печать в файл res_7.txt. В результате он будет заполнен следующей информацией

123456789............... (не выводится)

x=.0 y=.0000 e=.00000

x=.1 y=.0950 e=.00139

x=.2 y=.1715 e=.00245

x=.3 y=.2321 e=.00324

x=.4 y=.2793 e=.00380

x=.5 y=.3151 e=.00419

x=.6 y=.3413 e=.00442

...........................

x= 6.0 y=.0135 e=.00017

Анализ результатов показывает, что максимальное значение относительной погрешности равно 0.455% при x = 0.8 и значительно превышает требуемую величину. Поэтому расчёты должны быть повторены при меньшем значении шага интегрирования. Последовательно проведённые расчёты с различными значениями шага показывают, что заданная погрешность приближённого решения достигается только при шаге h = 0.01.

График численного решения рассматриваемой задачи Коши, полученный на экране монитора, представлен на рис.1.

Рис.1.

СПИСОК ЛИТЕРАТУРЫ

1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – 3-е изд., перераб. и доп. М.: БИНОМ. Лаборатория знаний, 2003. 632 с.

2. Воеводин В.А. Вычислительные основы линейной алгебры. М.: Наука, 1977. 303 с.

3. Волков Е.А. Численные методы. М.: Наука, 1982. 254 с.

4. Киреев В.И., Пантелеев А.В. Численные методы в примерах и задачах. М.: Высшая школа, 2004. 480 с.

5. Инженерные расчеты на ЭВМ: Справочное пособие. Под ред. В.А.Троицкого. Л.: Машиностроение, 1979. 288 с.

6. Бартеньев О.В. Фортран для профессионалов. Математическая библиотека IMSL. Часть 1. М.: Диалог–МИФИ, 2000. 448 с.

7. Бартеньев О.В. Фортран для профессионалов. Математическая библиотека IMSL. Часть 2. М.: Диалог–МИФИ, 2001. 320 с.

8. Бартеньев О.В. Фортран для профессионалов. Математическая библиотека IMSL. Часть 3. М.: Диалог–МИФИ, 2001. 368 с.

СОДЕРЖАНИЕ

Введение…………………………………………………………….….			3
Глава 1.	Вычисление определённых интегралов……………………	5
Глава 2.	Решение нелинейных уравнений….………………………..	13
Глава 3.	Решение систем линейных алгебраических уравнений……	31
Глава 4.	Интерполяция таблично заданных функций………………	52
Глава 5.	Аппроксимация таблично заданных функций……………	68
Глава 6.	Решение задачи Коши для обыкновенных дифференциальных уравнений 1-го порядка……………………………	83
Глава 7.	Решение задачи Коши для нормальных систем обыкновенных дифференциальных уравнений и уравнений высших порядков……………………………………………….	98

Список литературы…………………………………………………….			119