Кусочно-линейная интерполяция состоит в представлении таблично заданной функции на каждом отрезке между абсциссами узловых точек линейной зависимостью y = a 1+ a 2 x так, как это показано на рис.2. Коэффициенты a 1 и a 2 определяются для каждого отрезка [ xi –1, xi ] в отдельности из условий
.
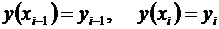В результате кусочно-линейная приближающая функция на отрезке [ xi –1, xi ] имеет вид
и является непрерывной, однако её первая производная оказывается уже кусочно-непрерывной функцией, которая в каждом узле интерполяции имеет точку разрыва первого рода. Это часто накладывает существенные ограничения на её дальнейшее использование.
| x | 0 | 1 | 2 | 3 | 4 |
| y | 2 | 0.5 | 1 | 4 | 4.5 |
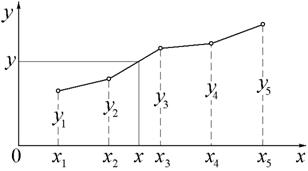
Рассмотрим работу метода на примере кусочно-линейной интерполяции таблично заданной функции и поиска её значения при аргументе х = 1.5.
Для решения этой задачи строятся линейные функции для каждого отрезка между узловыми точками таблицы:
для отрезка [0, 1] между первой и второй точками
,
для отрезка [1, 2] между второй и третьей точками
,
для отрезка [2, 3] между третьей и четвёртой точками
,
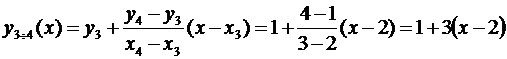для отрезка [3, 4] между четвёртой и пятой точками
.
Таким образом, табличная функция в случае кусочно-линейной интерполяции представляется в виде функции
Значение интерполирующей функции в заданной точке x = 1.5, принадлежащей отрезку [1, 2] будет y (1.5) = 0.5 + 0.5(1.5 – 1) = 0.75.
Многочлен Лагранжа (J.L.Lagrange, 1795)
Представляет собой случай полиномиального представления приближающей функции, когда она ищется в виде линейной комбинации базисных функций j k (x), которые должны быть определены для всего отрезка интерполяции [ x 1, xn ], линейно независимы, а их количество должно быть равно числу узлов таблично заданной функции
.
Коэффициенты a 1, a 2,..., an определяются исходя из условий равенства значений приближающей и исходной функций при табличных значениях аргумента, что сводит задачу к системе n линейных алгебраических уравнений относительно них, а в качестве функций j k (x) используются полиномы (n –1) степени
,
которые для пяти узловых точек записываются в виде
,
…………………………………………
.
Графики этих полиномов представлены на рис.3. Для каждого полинома характерно то, что для всех значений xi узловых точек он принимает нулевые значения, кроме k -ой, где его значение равно единице.
При таком выборе базисных функций коэффициенты приближающей функции оказываются ординатами таблично заданной функции, а сама она приобретает характерный для многочлена Лагранжа вид
.
Процесс построения интерполирующего многочлена Лагранжа для пяти узловых точек показан на рис.4.
| x | 0 | 1 | 2 | 3 |
| y | 2 | 0.5 | 1 | 4 |
Рассмотрим работу метода на примере интерполяции по Лагранжу таблично заданной функции и поиска её значения при х = 1.5.
Сначала строятся четыре базовых полинома:
,
,
.
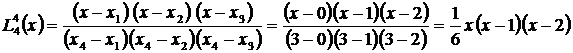Они позволяют записать интерполирующий многочлен Лагранжа в виде:
Для аргумента x = 1.5 многочлен Лагранжа даёт значение
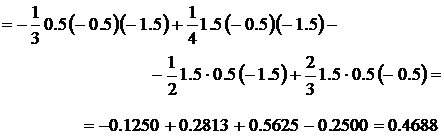
Интерполяция кубическим сплайном (I.J.Schoenberg, 1946)
Сплайнами называется широкий класс приближающих функций, конструируемых путем кусочной интерполяции с использованием различных функций, в число которых входят полиномы, в частности, кубический. При использовании кубического полинома табличная функция внутри каждого отрезка [ x 1, x 2], [ x 2, x 3],…,[ xi, xi+ 1],…,[ x n – 1, x n ] представляется следующим образом
,
,
……………………………………………………………………
,
……………………………………………………………………………
где нижние индексы интерполирующих функций, записанные через тире, указывают на номера узлов, между которыми проведен сплайн (см. рис.5).
Отрезки образуют область определения сплайна. Вычисление его коэффициентов ai (i =1,2,…,4(n –1)) осуществляется исходя из следующих условий. По определению, значения сплайна в узловых точках должны совпадать с соответствующими значениями таблично заданной функции
,
.
Эти условия дают (2 n –2) уравнений для определения коэффициентов сплайна.
Кроме этого, требуется, чтобы полином данного отрезка сопрягался с соседними полиномами, как по углу наклона касательной в узловых точках, так и по радиусу кривизны. Сопряжение по углу наклона соответствует равенству значений первых производных соседних полиномов в каждой узловой точке, а по радиусу – вторых производных. Это даёт ещё по два условия для каждой внутренней узловой точки
,
т.е. получается ещё (2 n –4) уравнений. Таким образом, приведенные выше соотношения дают (4 n –6) уравнений для определения коэффициентов ai и для доопределения системы не хватает ещё двух уравнений. С целью построения недостающих уравнений можно задавать в граничных точках значения угла наклона касательной (исходя из физической сути задачи или с помощью интерполяции по 4-м крайним точкам с последующим вычислением производной)
.
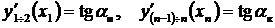Возможны и иные способы задания граничных условий. Например, можно задавать граничные значения не первых, а вторых производных
.
Особый способ, называемый условием «нет узла» или «запрет стыка», состоит в приравнивании третьих производных полиномов на стыке двух крайних отрезков
.
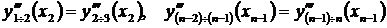Перечисленные условия дают систему из 4(n –1) линейных алгебраических уравнений, позволяющую вычислить коэффициенты для каждого отрезка сплайна. Полученная интерполирующая функция будет непрерывной и гладкой вместе со своей первой производной, её вторая производная будет только непрерывной функцией, которая имеет точки излома в местах сопряжения сплайнов, т.е. в узловых точках.
| x | 0 | 1 | 3 |
| y | 2 | 0.5 | 4 |
Рассмотрим работу метода на примере таблично заданной функции (см. приведённую таблицу) и поиска значения этой функции при х = 1.5.
Для решения задачи интерполяции заданной функции кубическими сплайнами требуется составить систему из 8-ми уравнений, позволяющую определить коэффициенты сплайнов для каждого из отрезков [0, 1] и [1, 3]
,
.
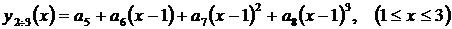Их производные, необходимые для формирования системы, имеют вид
,
,
,
.
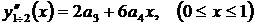Тогда условия формирования сплайнов, записанные в последовательности узловых точек, будут выглядеть следующим образом
точка №1 (x = 0): 
,
точка №2 (x = 1): 
,
,
,
,
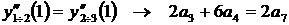точка №3 (x = 3): 
,
.
Недостающие значения тангенсов углов наклона касательных в крайних узловых точках могут быть вычислены из геометрических соображений, основанных на приближённом построении интерполирующей кривой (см. рис.6)
.
Таким образом, система уравнений, определяющая коэффициенты кубических сплайнов, будет иметь вид
.
Её решение осуществляется каким-либо известным способом решения систем линейных алгебраических уравнений. В результате получается следующее её решение
a 1= 2, a 2=–2.5, a 3= 0.9267, a 4= 0.07333,
a 5= 0.5, a 6= –0.4267, a 7= 1.147, a 8= –0.02917.
При этом искомые сплайны будут иметь вид
,
,
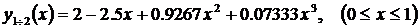а интерполирующая функция может быть записана как
.
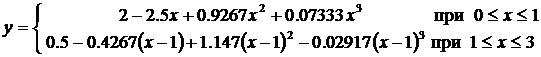Её значения при х = 1.5 будет
.
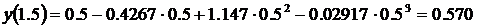Программное обеспечение. В математической библиотеке IMSL имеется большой набор средств для интерполяции функций, из которого можно выделить подпрограмму Csdec и функцию Csval
Subroutine Csdec(Ndt,Xdt,Fdt,Ilt,Dlt,Irt,Drt,Brk,CSc),
Function Csval(x,Nint,Brk,CSc).
Подпрограмма Csdec предназначена для вычисления коэффициентов кубического сплайна, а функция Csval – для вычисления значений интерполирующего сплайна при заданном значении аргумента.
В качестве формальных параметров в подпрограмме и функции используются:
Ndt - количество узловых точек интерполяции (Integer*4);
Xdt - одномерный массив из Ndt элементов, содержащий значения (не обязательно в порядке возрастания, но не должно быть совпадающих) абсцисс узловых точек (Real*4);
Fdt - одномерный массив из Ndt элементов, содержащий значения ординат соответствующих узловых точек, описанных в массиве Xdt (Real*4);
Ilt - тип условия в левой граничной точке (Integer*4);
Dlt - значение производной в левой граничной точке (Real*4);
Irt - тип условия в правой граничной точке (Integer*4);
Drt - значение производной в правой граничной точке (Real*4);
Brk - одномерный массив из Ndt элементов, содержащий координаты точек сопряжения отрезков области определения сплайна, включая граничные точки – фактически значения из массива Xdt (Real*4);
CSc - двумерный массив 4´Ndt, содержащий значения коэффициентов интерполирующих кубических сплайнов (Real*4);
x - значение аргумента, для которого вычисляется значение приближающей функции (Real*4);
Nintv - число отрезков в области определения сплайна, равное (Ndt–1) (Integer*4).
Признаки типов граничных условий (Ilt и Irt) принимают следующие значения:
· 0 - условие «нет узла» (значения Dlt и Drt игнорируются);
· 1 - задаются значения первой производной (параметры Dlt и Drt);
· 2 - задаются значения второй производной (параметры Dlt и Drt).
Для аргументов двойной точности (Real*8) используются подпрограмма с именем DCsdec и функция с именем DCsval.
В качестве исходного материала для выполнения заданий лабораторной работы предложены относительно простые тексты программ, реализующих следующие методы:
- кусочно-линейную интерполяцию
Subroutine Lin_int(n,X,Y,xt,yt);
- интерполяцию многочленом Лагранжа
Subroutine Lagrang(n,X,Y,xt,yt);
- интерполяцию кубическим сплайном
Subroutine Spline(n,X,Y,tgn,tgk,m,A,*);
Function Spline_0(n,X,m,A,xt).
В качестве формальных параметров в подпрограммах интерполяции таблично заданных функций используются:
n - количество узловых точек интерполяции (Integer*4);
X - одномерный массив из n элементов, содержащий значения абсцисс узловых точек (Real*4);
Y - одномерный массив из n элементов, содержащий значения ординат узловых точек (Real*4);
xt - значение аргумента, для которого вычисляется значение приближающей функции (Real*4);
yt - вычисленное значение приближающей функции (Real*4);
* - номер метки оператора, которому необходимо передать управление, если исходная система уравнений неразрешима;
tgn - значение тангенса угла наклона касательной к приближающей функции в первой узловой точке (Real*4);
tgk - значение тангенса угла наклона касательной к приближающей функции в последней – n-ой узловой точке (Real*4);
m - количество коэффициентов в записи интерполирующих кубических сплайнов (m=4´(n-1)) (Integer*4);
A - одномерный массив из m элементов, содержащий значения коэффициентов интерполирующих кубических сплайнов (Real*4);
При интерполяции кубическими сплайнами используются подпрограммы Spline и Spline_0. Подпрограмма Spline позволяет определить значения коэффициентов сплайнов, а Spline_0 – вычислить значения приближающей функции при заданном значении аргумента.
Пример выполнения задания. Одним из методов интерполяции на отрезке [1,4] сформировать образ кривой, являющейся графиком функции
y = x 3 – 7.3 x 2+ 16.8 x – 12.2
и заданной в табличной форме. При этом точки интерполяции в количестве 11 штук равномерно распределить на заданном отрезке.
Решение. В качестве метода интерполяции можно выбрать кусочно-линейную. Графики исходной и интерполирующей функций будут строиться на экране монитора по 101-й точке. Визуализацию решения следует разбить на два этапа. На первом этапе вывести на экран монитора узловые точки и график интерполирующей функции, а на втором – графики исходной и интерполирующей функций. Текст программы, реализующий приведенный сценарий визуализации процесса интерполяции функции показан ниже.
Character Nt1*47, Nt2*43
Real*4 Xp(11),Yp(11),Xi(101),Yi(101),Ym(2,101)
a = 1.
b = 4.
Do i=1,11
x = a + (b-a)*(i-1)/10
Xp(i) = x
Yp(i) = x**3 - 7.3*x**2 + 16.8*x - 12.2
Enddo
Do i = 1, 101
x = a + (b-a)*(i-1)/100
Call Lin_int(11,Xp,Yp,x,y)
Xi(i) = x
Yi(i) = y
Enddo
Nt1 = 'Узловые точки и график интерполирующей функции.'
Call Graf_1P(101,Xi,Yi,11,Xp,Yp,'x','y',Nt1,47)
Do i = 1, 101
x = Xi(i)
Ym(1,i) = x**3 - 7.3*x**2 + 16.8*x - 12.2
Ym(2,i) = Yi(i)
Enddo
Nt3 = 'Графики исходной и интерполирующей функции.'
Call Graf_1_9(2,101,Xi,Ym,'x','y',Nt2,43)
Stop
End
Получающиеся на экране монитора графики исходной функции, узловых точек, интерполирующей функции и их взаимное расположение представлены на рис.7 и 8.
Рис.7.
Рис.8.
Результаты кусочно-линейной интерполяции – неудовлетворительны (см. рис.8). Для улучшения качества интерполяции исходной функции можно применить многочлен Лагранжа, воспользовавшись подпрограммой Lagrang. Текст программы в этом случае подобен приведённой выше.
Character Nt1*47, Nt2*43
Real*4 Xp(11),Yp(11),Xi(101),Yi(101),Ym(2,101)
a = 1.
b = 4.
Do i=1,11
x = a + (b-a)*(i-1)/10
Xp(i) = x
Yp(i) = x**3 - 7.3*x**2 + 16.8*x - 12.2
Enddo
Do i = 1, 101
x = a + (b-a)*(i-1)/100
Call Lagrang(11,Xp,Yp,x,y)
Xi(i) = x
Yi(i) = y
Enddo
Nt1 = 'Узловые точки и график интерполирующей функции.'
Call Graf_1P(101,Xi,Yi,11,Xp,Yp,'x','y',Nt1,47)
Do i = 1, 101
x = Xi(i)
Ym(1,i) = x**3 - 7.3*x**2 + 16.8*x - 12.2
Ym(2,i) = Yi(i)
Enddo
Nt3 = 'Графики исходной и интерполирующей функции.'
Call Graf_1_9(2,101,Xi,Ym,'x','y',Nt2,43)
Stop
End
Результаты работы программы показаны на рис.9 и 10.
Рис.9.
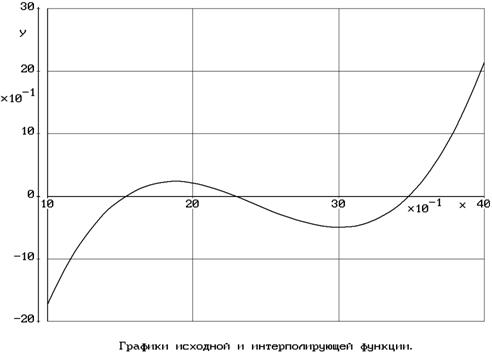
Рис.10.
График многочлена Лагранжа на рис.10 визуально совпадает с графиком исходной функции. На этом можно остановиться. В противном случае следовало бы применить интерполяцию сплайнами с реализацией этого процесса в виде программы
Character Nt1*47, Nt2*43
Real*4 Xp(11),Yp(11),Xi(101),Yi(101),Ym(2,101),Ai(40)
a = 1.
b = 4.
Do i=1,11
x = a + (b-a)*(i-1)/10
Xp(i) = x
Yp(i) = x**3 - 7.3*x**2 + 16.8*x - 12.2
EndDo
Call Spline(11,Xp,Yp,5.0,6.5,40,Ai,*10)
Do i = 1, 101
x = a + (b-a)*(i-1)/100
Xi(i) = x
Yi(i) = Spline_0(11,Xp,40,Ai,x)
EndDo
Nt1 = 'Узловые точки и график интерполирующей функции.'
Call Graf_1P(101,Xi,Yi,11,Xp,Yp,'x','y',Nt1,47)
Do i = 1, 101
x = Xi(i)
Ym(1,i) = x**3 - 7.3*x**2 + 16.8*x - 12.2
Ym(2,i) = Yi(i)
EndDo
Nt3 = 'Графики исходной и интерполирующей функции.'
Call Graf_1_9(2,101,Xi,Ym,'x','y',Nt2,43)
Go to 12
10 Write(*,*) '*** Интерполяция невозможна ***'
12 Stop
End
Глава 5. АППРОКСИМАЦИЯ ТАБЛИЧНО ЗАДАННЫХ ФУНКЦИЙ
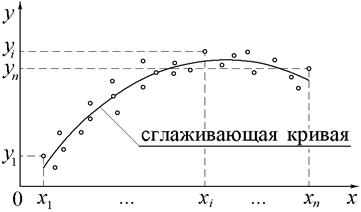Интерполяция на практике используется только в тех случаях, когда значения координат узлов таблично заданной функции не искажены случайными ошибками. Наличие ошибок в значениях таблично заданной функции приводит к неправильному представлению о поведении реальной функции и, как следствие этого, делает бессмысленной её интерполяцию. В этом случае рекомендуется строить «сглаживающую» приближающую функцию, отражающую физику моделируемого процесса. Её график не обязан проходить через все узловые точки табличной функции, как показано на рис.1. Построение таких приближающих функций носит название аппроксимации.
Через множество узловых точек таблично заданной функции можно провести бесконечное количество аппроксимирующих кривых. Задача выбора единственной из них определяется двумя основными моментами:
- выбор аналитических зависимостей, отражающих физику взаимосвязи аргумента и реальной функции, когда должен быть определён общий вид приближающей функции;
- выбор критерия достоверности описания реальной функции с помощью выбранных зависимостей.
Существует множество подходов к построению вида приближающей функции, как функции с параметрами. Одним из них является выбор в качестве аппроксимирующей зависимости линейной комбинации некоторых известных аналитических функций. Вместе они должны отражать суть физического процесса, описываемого исходной функцией, и быть линейно независимыми на отрезке аппроксимации [ x 1, x n ]
.
Функции φ k (x) часто выбираются в виде полиномов, частным случаем которых являются степенные функции
φ 1(x) = 1, φ 2(x) = x, φ 3(x) = x 2, φ 4(x) = x 3,…,
в виде тригонометрических косинусов
,
или в любом другом удобном для исследователя виде.
Другим подходом к построению приближающей функции является её представление сплайнами. Это избавляет исследователя от необходимости подбирать аналитические функции для аппроксимирующей зависимости и часто даёт результат, отвечающий всем требованиям, которые предъявляются к процессу аппроксимации.
В качестве критерия достоверности описания реальной функции Гауссом (1794) и Лежандром (A.M.Legendre, 1805) было предложено использовать сумму квадратов отклонений значений аппроксимирующей функции от ординат узлов таблично заданной
,
где отклонение от каждой узловой точки Δ i, показанное на рис.2, вычисляется как
.
Сумма квадратов отклонений F при таком представлении является квадратичной функцией от параметров аппроксимации c 1, c 2,..., c m. Очевидно, что чем меньше значение функции F, тем лучше выбранная аппроксимирующая функция описывает реальную функцию. Следовательно, задача аппроксимации сводится к определению значений параметров c 1, c 2, ..., c m, которые минимизируют значение критерия – функции F. Этот приём получил название «метод наименьших квадратов».
Необходимым условием экстремума квадратичной функции F является равенство нулю всех её частных производных по параметрам c 1, c 2, ..., c m
.
Можно показать, что для функции F, являющейся суммой квадратов отклонений, достаточные условия существования её минимума в стационарной точке выполняются тождественно. Поэтому необходимыми условиями существования экстремума функции F можно пользоваться как условиями её минимума, что позволяет привести задачу аппроксимации n значений табличной функции к задаче решения системы из m линейных алгебраических уравнений относительно этих параметров с симметричной матрицей
,
где
,
.
Работа метода может быть проиллюстрирована на примере аппроксимации функции, заданной 8-ю узловыми точками на рис.3, и поиска её значения при х = 1.5.
Для построения зависимости, аппроксимирующей таблично или графически заданную функцию, исследователь должен подобрать аналитические функции, которые своей комбинацией отражают описываемый процесс. В данном случае исходная функция может быть описана как комбинация двух функций. Первая из них должна отражать обратно пропорциональную зависимость функции от аргумента в диапазоне от 0 до 2, а вторая – прямо пропорциональную зависимость в диапазоне от 2 до 4. Таким образом, в качестве аппроксимационной зависимости может быть принята следующая
.
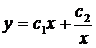Необходимо заметить, что данное представление аппроксимирующей зависимости не является единственным. Можно подобрать и другие комбинации элементарных функций, которые отражают общий характер рассматриваемой табличной функции.
В соответствии с приведённым выше алгоритмом сумма F квадратов отклонений ординат аппроксимирующей функции от ординат узловых точек записывается в виде
Вычисления по этой формуле удобнее выполнять, сняв с графика координаты узловых точек и сформировав из них следующую таблицу.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| x | 0.5 | 0.5 | 1 | 1.5 | 1.5 | 2.5 | 3.5 | 4 |
| y | 0.9 | 0.8 | 0.5 | 0.5 | 0.4 | 0.4 | 0.5 | 0.5 |
В этом случае сумма квадратов отклонений будет
а её частные производные по параметрам c 1 и c 2, соответственно
Исходя из условия равенства нулю полученных частных производных, решение задачи сводится к решению системы из двух линейных алгебраических уравнений
.
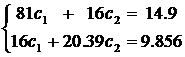Эта система имеет следующее решение
c 1= 0.1047, c 2= 0.4013.
Таким образом, аппроксимирующая функция имеет вид
,
а её значение при х = 1.5 будет y (1.5) = 0.4246.
Программное обеспечение. В математической библиотеке IMSL имеется модуль Fnlsq, обеспечивающий аппроксимацию по методу наименьших квадратов при помощи пользовательских базисных функций:
Subroutine Fnlsq(Fi,Icp,Nbs,Ndt,Xdt,Fdt,Iwt,Wgh,C,Ss).
В качестве формальных параметров здесь используются:
Fi - имя внешней подпрограммы-функции, в которой вычисляются значения базисных функций (Real*4);
Icp - параметр отсечения (Integer*4), принимающий значения 0 или 1, смысл которого в том, что при Icp=0 аппроксимирующая зависимость принимается в виде
C(1)*Fi(1,x)+C(2)*Fi(2,x)+…+C(Nbs)*Fi(Nbs,x),
а при Icp=1 – в виде
C(1)+C(2)*Fi(1,x)+C(3)*Fi(2,x)+…+C(Nbs+1)*Fi(Nbs,x);
Nbs - количество базисных функций (Integer*4);
Ndt - количество узловых точек аппроксимации (Integer*4);
Xdt - значения абсцисс узловых точек (одномерный массив из Ndt элементов) (Real*4);
Fdt - значения ординат узловых точек (одномерный массив из Ndt элементов) (Real*4);
Iwt - признак (Integer*4) использования весовых коэффициентов узлов, смысл которого заключается в том, что минимизируемая функция F может вычисляться с учётом значимости отдельных узлов, учитываемой посредством узловых весов wi (задаваемых, неотрицательных величин) в формуле
,
причем при Iwt=0 все значения wi = 1 (веса не используются), а при Iwt=1 веса задаются в массиве Wgh;
Wgh - вектор весов узловых точек (одномерный массив из Ndt элементов) (Real*4), причем если Iwt=0, то массив не используется и может иметь длину 1;
C - вектор коэффициентов аппроксимирующей зависимости (одномерный массив из Icp+Nbs элементов) (Real*4), причем если Icp=1, то элемент C(1) содержит отсечение, а C(Icp+i) – коэффициет i -й базисной функции;
Ss - вычисленная сумма F квадратов отклонений аппросимирующей зависимости в узлах (Real*4).
Подпрограмма-функция Fi оформляется в виде
Function Fi(k,x)
select case(k)
case(1)
Fi =..............
..................
case(Nbs)
Fi =..............
end select
Return
End
где k - номер базисной функции (k=1,2,…,Nbs) (Integer*4);
x - значение аргумента базисной функции (Real*4).
При обнаружении линейной зависимости базисных функций выдается соответствующее сообщение, и выполнение программы прекращается.
Для аргументов двойной точности (Real*8) используется подпрограмма с именем DFnlsq.
В качестве исходного материала для выполнения заданий лабораторной работы предложен текст программы, реализующей метод наименьших квадратов:
Subroutine Mnk(n,X,Y,m,C,Func_Mnk,*).
В качестве параметров в подпрограмме используются:
n, m - количество узловых точек аппроксимации и коэффициентов аппроксимирующей зависимости (Integer*4);
X, Y - абсциссы и ординаты узловых точек (одномерные массивы из n элементов) (Real*4);
Func_Mnk - имя подпрограммы для вычисления значений базисных функций аппроксимирующей зависимости;
C - матрица коэффициентов аппроксимирующей зависимости (одномерный массив из m элементов) (Real*4);
* - метка оператора, которому передается управление, если матрица системы вырождена.
Подпрограмма Func_Mnk оформляется в виде:
Subroutine Func_Mnk(m,x,Fi)
Real*4 Fi(m)
Fi(1)=..............
....................
Fi(m)=..............
Return
End
Здесь x - значение аргумента, при котором вычисляются базисные функции (Real*4);
Fi - значения базисных функций при заданном аргументе x (одномерный массив размерностью m) (Real*4).
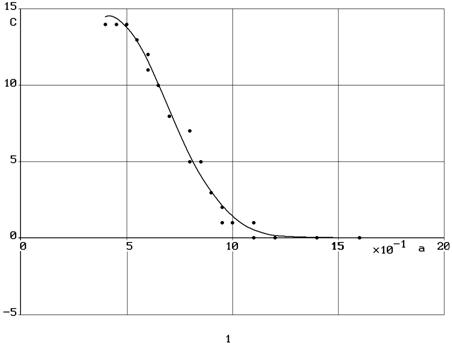
Пример выполнения задания. Построить приближающую функцию, описывающую изменение процентного содержания С [%] окиси углерода в выхлопе двигателя Р11-Ф2-300 в зависимости от степени обогащённости топливной смеси α, используя экспериментальные данные, которые приведены на рис.4. В качестве аппроксимирующей функции (при α0= 0.4) использовать зависимость
.
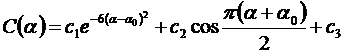Рис.4.
Решение. Для решения задачи построения приближающей функции формируется программа, текст которой приводится ниже
External Fu
Real*4 Xm(20),Ym(20),Cm(3),Fi(3),Xgr(101),Ygr(101)
Open(5, file='dat_5.txt')
Read(5, 1) (Xm(i), Ym(i), i = 1, 20)
1 Format(/(8X, 2F10.4))
Call Mnk(20,Xm,Ym,3,Cm,Fu,*4)
Do 2 n = 1, 101
x = 0.4 + 0.012*(n-1)
Call Fu(3,x,Fi)
y = Cm(1)*Fi(1)+Cm(2)*Fi(2)+Cm(3)*Fi(3)
Xgr(n) = x
2 Ygr(n) = y
Call Graf_1P(101,Xgr,Ygr,20,Xm,Ym,'a','C','1',1)
Go to 5
4 Write(*,*) ' *** Аппроксимация невозможна ***'
5 Close(5)
Stop
End
Subroutine Fu(m, Alfa, Fi)
Real*4 Fi(m)
Pi = 3.141592
Ao = 0.4
Fi(1) = exp(-6.*(Alfa-Ao)**2)
Fi(2) = cos(Pi*(Alfa+Ao)/2)
Fi(3) = 1.
Return
End
Исходные данные в файле dat_5.txt представляют собой координаты точек, снятые с графика и оформленные в виде
Исходные данные с графика
0.4 14.0
0.45 14.0
0.5 14.0
0.55 13.0
0.6 12.0
0.6 11.0
0.65 10.0
0.7 8.0
0.8 7.0
0.8 5.0
0.85 5.0
0.9 3.0
0.95 2.0
0.95 1.0
1.0 1.0
1.1 1.0
1.1 0.0
1.2 0.0
1.4 0.0
1.6 0.0
В результате решения задачи на экран монитора выводится график (см. рис.5) найденной приближающей функции в виде:
|
Глава 6. РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 1-ГО ПОРЯДКА
Обыкновенное дифференциальное уравнение 1-го порядка
связывает независимую переменную x, искомую функцию y и её производную. Решение дифференциального уравнения заключается в отыскании функции y = y (x), обращающей это уравнение в тождество на конечном или бесконечном интервале (a, b). Различают общее и частные решения дифференциального уравнения. Общее решение уравнения имеет вид y = y (x, C), где C – произвольная постоянная интегрирования. Его графическим отображением является семейство кривых (см. рис.1), называемых интегральными. Каждая интегральная кривая является отображением частного решения, соответствующего своему значению постоянной C. Для выделения частного решения из множества кривых общего решения необходимо задать начальное условие
.
Такая постановка задачи отыскания решения дифференциальных уравнений называется задачей Коши 
(A.L.Cauchy, 1789–1857). Для существования единственного решения задачи Коши необходимо и достаточно существование и ограниченность правой части дифференциального уравнения f (x, y) и её частной производной ¶ f (x, y)/¶ y в некоторой окрестности начальной точки (x 0, y 0).
Для численного решения задачи Коши существует множество методов, которые условно делятся на две 
группы: одношаговые и многошаговые. Все эти методы позволяют получить искомое решение дифференциального уравнения в виде таблично заданной функции, в той или иной мере согласующееся с истинным частным решением (см. рис.2). Эти группы методов различаются объёмом информации, которая используется для вычисления координат очередной точки табличной функции. Одношаговые методы используют значения функции и её производной только в одной предыдущей точке, в то время как многошаговые – в нескольких. К одношаговым методам решения задачи Коши относятся метод Эйлера, модифицированный метод Эйлера, методы Рунге–Кутта и другие.
Метод Эйлера (L.Euler, 1768)
Он является старейшим методом решения задачи Коши и заключается в последовательном применении следующих формул
,
,
,
геометрическая интерпретация которых при k = 0 представлена на рис.3. В точке (x 0, y 0)вычисляется значение производной dy/dx через f (x, y), которое определяет тангенс угла наклона касательной к графику точного решения задачи Коши. Следующая точка численного решения определяется как точка на этой касательной с абсциссой x 1 = x 0+ h. В компактном виде для k = 0, 1, 2,… эти соотношения записываются следующим образом
,
.
Метод Эйлера относится к методам первого порядка точности, поскольку его решение совпадает с истинным только в том случае, когда последнее является линейной функцией y = a 1+ a 2 x. Его абсолютная погрешность ε абс(xk +1, h) на каждом шаге пропорциональна величине h 2. Это обусловлено тем, что в качестве направления, определяющего положение следующей точки численного решения, используется касательная в левой точке каждого отрезка [ xk, xk +1]. На рис.3 видно, что для получения более точного численного решения недостаточно знания параметров функции в единственной левой точке отрезка [ xk, xk +1]. Требуется собрать дополнительную информацию о её поведении на отрезке интегрирования для отыскания решения при x = xk +1 с меньшей погрешностью. Для этого можно использовать некоторые промежуточные направления, определяемые касательными к графику неизвестного точного решения в характерных точках рассматриваемого отрезка (крайние точки, середина отрезка и т.д.).
