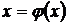Метод основывается на приведении исходного уравнения к форме

.

Это преобразованиеможет быть выполнено многими способами. Например, уравнение

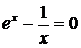
может быть преобразовано как

 или .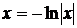

Далее процесс уточнения корня строится по итерационной схеме

…………

……………

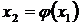
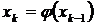
где x ₀ – начальное приближенное значение корня на отрезке [ a, b ].

Если последовательностьзначений x _k (k = 0, 1, 2,...) имеет конечный предел, то итерационный процесс сходится к точному значению корня x _тза бесконечно большое число шагов. Абсолютная и относительная погрешности найденного значения корня на k -ом шаге (x_k) могут быть получены из выражений

,     ,

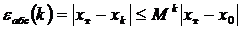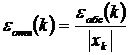где

, , .

Первое из этих выражений может иметь другие формы записи

, .

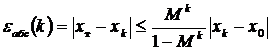Приведённые формулы для вычисления погрешностей требуют решения дополнительной задачи поиска максимума модуля первой производной функции φ (x) на отрезке локализации корня [ a, b ]. Поэтому на практике итерации завершают при выполнении одного из условий:

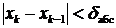или ,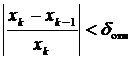

где δ _абс и δ _отн – задаваемые абсолютная и относительная разницы между соседними значениями приближения корня, соответственно. В этом случае надо помнить, что истинная погрешность определения корня может заметно отличаться от δ _абс или δ _отн. Поэтому после завершения поиска корня необходимо вычислить истинное значение погрешности решения по приведённым формулам для ε _абс или ε _отн.

Может случиться так, что последовательность приближённых значений x _k (k = 0, 1, 2,...) корня x _т не имеет предела. В этом случае метод расходится, и описанная итерационная схема не может быть применена для решения уравнения. Анализ выражения для ε _абс позволяет сформулировать условие сходимости итераций. Очевидно, для того, чтобы погрешность ε _абс при стремлении k к бесконечности стремилась к нулю и итерации сходились к точному решению, надо обеспечить выполнение следующего неравенства

,

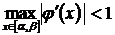которое на практике обычно заменяется на упрощённое

.

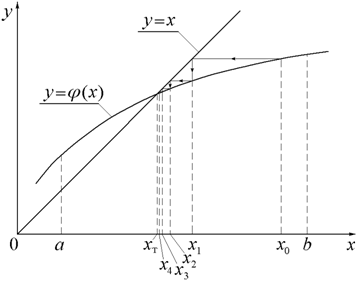
Рис.2.                                                 Рис.3.

Процесс уточнения корня уравнения методом простых итераций может быть проиллюстрирован графически.

Как видно на рис.2, для выбранной на отрезке [ a, b ] начальной точки x ₀ вычисляется значение функции j (x ₀). Абсцисса этой точки с помощью графика функции y = x преобразуетсявновое приближение переменной x ₁. Далее процесс повторяется, и находятся значения x ₂, x ₃,..., x _k,... до тех пор, пока не будет выполнено условие завершения итерационного процесса. В данном случае итерационный процесс сходится. На рис.3 показана ситуация, когда метод итераций расходится. Каждое новое значение x _k отстоит всё дальше от точного решения уравнения x _ти заданная погрешность вычисления недостижима. Такая ситуация характерна для неудачного преобразования уравнения f (x) = 0 к уравнению x = j (x).

Исходя из этого, можно указать способ преобразования исходного уравнения f (x) = 0 к форме, обеспечивающей сходимость итераций. Он основан на том, что исходное уравнениеравносильно уравнению x = x + λ f (x), где λ – отличная от нуля произвольная постоянная, которая выбирается из приближённого условия сходимости итераций , считая j (x) = x + λ f (x).

Рассмотрим работу метода на примере поиска приближённого значения корня уравнения

x ³ – 7.3 x ² + 16.8 x – 12.2 = 0,

лежащего на отрезке [1, 2] и оценки погрешности его определения.

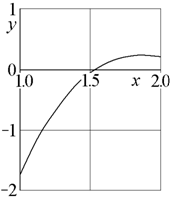
На первом этапе необходимо построить график левой части уравнения, для чего вычисляются её значения в трёх базовых точках

f (1.0) = 1.0³ – 7.3·1.0² + 16.8·1.0 – 12.2 = – 1.70,

f (1.5) = 1.5³ – 7.3·1.5² + 16.8·1.5 – 12.2 = – 0.05,

f (2.0) = 2.0³ – 7.3·2.0² + 16.8·2.0 – 12.2 = 0.20.

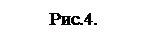Как видно из рис.4, в качестве начального приближения корня рассматриваемого уравнения следует взять x ₀= 1.5. Следуя алгоритму метода итераций, требуется преобразовать исходное уравнение к виду

x = x + λ (x ³ – 7.3 x ² + 16.8 x – 12.2),

где

φ (x) = x + λ (x ³ – 7.3 x ² + 16.8 x –12.2),

а

= 1+ λ (3 x ² – 14.6 x + 16.8),

и найти значение множителя λ. Для этого можно воспользоваться условием сходимости метода

.

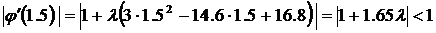Отсюда                          –1 < 1 + 1.65 λ < 1,

–2 < 1.65 λ < 0,

–1.212 < λ < 0,

что позволяет выбрать λ = –0.6.

С использованием в качестве начального значения x ₀ = 1.5 выполняется первая итерация

x ₁ = 1.5– 0.6(1.5³–7.3·1.5² + 16.8·1.5 – 12.2) = 1.53.

Выполнение второй итерации даёт следующий результат

x ₂ = 1.53– 0.6(1.53³–7.3·1.53² + 16.8·1.53 – 12.2) = 1.5318,

а третья и четвёртая итерации соответственно дают

x ₃ = 1.5320, x ₄ = 1.53202.