 .
.
Таким образом, если в задаче требовалось бы вычислить значение корня с относительной разностью δ отн=0.00002, то уточнение значения корня можно прекратить. Однако истинное значение относительной погрешности вычисления будет определяться по формуле
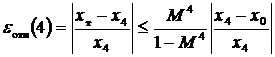 .
.
Для определения значения M, предполагая монотонность первой производной функции φ (x) на отрезке [ x 0, x 4], достаточно вычислить её значения при x 0 = 1.5 и x 4 = 1.53202 и взять из них наибольшее по модулю
 = 1 – 0.6(3·1.52 – 14.6·1.5 + 16.8) = 0.01,
= 1 – 0.6(3·1.52 – 14.6·1.5 + 16.8) = 0.01,
 = 1 – 0.6(3·1.532022 – 14.6·1.53202 + 16.8) = 0.11574,
= 1 – 0.6(3·1.532022 – 14.6·1.53202 + 16.8) = 0.11574,
М = 0.11574,
откуда
 .
.
Аналогичную оценку относительной погрешности можно получить, рассмотрев только последнюю итерацию
 = 1 – 0.6(3·1.53202 – 14.6·1.5320 + 16.8) = 0.11567,
= 1 – 0.6(3·1.53202 – 14.6·1.5320 + 16.8) = 0.11567,
 = 1 – 0.6(3·1.532022 – 14.6·1.53202 + 16.8) = 0.11574,
= 1 – 0.6(3·1.532022 – 14.6·1.53202 + 16.8) = 0.11574,
М = 0.11574,
откуда
 .
.
Полученные значения оценки относительной погрешности отличаются друг от друга в два раза. Однако это не должно вызывать недоумения, поскольку полученные числа – не значения погрешности, а всего лишь её оценки сверху.
Метод Ньютона (I.Newton, 1669, Mr.Raphson, 1720)
В данном методе каждое новое приближение к значению корня уравнения f (x) = 0 ищется по следующей итерационной схеме


………………….
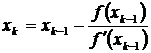
………………….
где x 0 – первоначальное приближенное значение корня, взятое с отрезка [ a, b ] локализации точного решения уравнения.
Если последовательностьзначений x k (k = 0, 1, 2,...) сходится к точному значению корня x т, то абсолютная погрешность значения корня на k -ом шаге (xk) определяется выражением
 ,
,
где
 ,
,  ,
,  ,
,  .
.
Вычисление относительной погрешности и формулировка условия окончания процесса уточнения значения корня осуществляется так же, как это было описано выше в методе итераций. Аналогично формулируется и условие сходимости метода Ньютона
 .
.
При решении практических задач точное значение x т корня уравнения неизвестно. Поэтому вместо приведённой формулы для абсолютной погрешности используют её аналоги
 ,
,  ,
,
где  ,
,  в первом случае и
в первом случае и 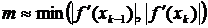 ,
,  во втором.
во втором.
А для проверки итерационной схемы на сходимость неравенство
 ,
,
где
 ,
,
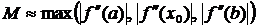 .
.

 Графическая интерпретация работы метода Ньютона представлена на рис.5. Из точки на кривой y = f (x), имеющей абсциссу x 0, проводится касательная до пересечения с осью 0 x. Абсцисса точки пересечения принимается за новое приближение значения x 1 корня уравнения f (x) = 0. В случае сходимости последовательности вычисляемых значений x 0, x 1,…, x k,… процесс продолжается до тех пор, пока не выполнится условие окончания процесса уточнения значения корня.
Графическая интерпретация работы метода Ньютона представлена на рис.5. Из точки на кривой y = f (x), имеющей абсциссу x 0, проводится касательная до пересечения с осью 0 x. Абсцисса точки пересечения принимается за новое приближение значения x 1 корня уравнения f (x) = 0. В случае сходимости последовательности вычисляемых значений x 0, x 1,…, x k,… процесс продолжается до тех пор, пока не выполнится условие окончания процесса уточнения значения корня.
Методы сужения отрезка [ a, b ], к которым относятся метод хорд, метод половинного деленияи другие, не имеют ограничений на функцию f (x), присущих методам последовательного уточнения.
Метод половинного деления (метод бисекций)
Работа метода иллюстрируется на рис.6. Отрезок локализации [ a, b ] корня делится пополам x 1= (a + b)/2 и в полученной точке вычисляется значение функции. Если f (x 1) = 0, то корень найден и расчёты прекращают. В противном случае выбирается новый отрезок, содержащий корень уравнения, из отрезков [ a, x 1] и [ x 1, b ]. На концах искомого отрезка функция f (x) должна иметь значения разного знака. Для этого проверяется условие f (a) f (x 1) < 0. При его выполнении в качестве нового отрезка принимается отрезок [ a, x 1], в противном случае – [ x 1, b ]. Процесс вычисления значения корня продолжается до тех пор, пока не будет выполнено требование к точности его определения. В данном случае оценка абсолютной погрешности определения корня

совпадает с длиной отрезка его последней локализации. В свою очередь относительная погрешность вычисляется как
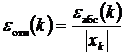 .
.
При этом за значение корня принимается либо одна из границ суженного отрезка [ a, b ], либо его середина.
Алгоритм работы метода может быть проиллюстрирован на примере рассмотренного выше уравнения
x 3 – 7.3 x 2 + 16.8 x – 12.2 = 0.
В качестве отрезка локализации выбирается отрезок [1.5, 1.6], содержащий первый корень уравнения (см. рис.4). На первом шаге уточнения корня вычисляются значения функции на границах выбранного отрезка
f (1.5) = 1.53 – 7.3·1.52+ 16.8·1.5 – 12.2 = – 0.05,
f (1.6) = 1.63 – 7.3·1.62+ 16.8·1.6 – 12.2 = 0.088.
Затем в середине интервала x 1 = 1.55 также вычисляется значение функции
f (1.55) = 1.553 – 7.3·1.552+ 16.8·1.55 – 12.2 = 0.0256.
Так как эта точка не соответствует корню уравнения, то определяется новый отрезок его локализации. Для этого проверяется знак произведения значений функции на левой границы отрезка локализации корня и в его центре f (1.5) f (x 1). Из расчётов видно, что это произведение меньше нуля, значит, в качестве нового отрезка локализации корня должен приниматься отрезок [1.5, 1.55].
Для выполнения второго шага уточнения корня значения функции на границах нового отрезка локализации считать не нужно, они уже известны: f (1.5) = – 0.05; f (1.55) = 0.0256. Достаточно вычислить её значение в середине нового отрезка локализации x 2 = 1.525
f (1.525) = 1.5253 – 7.3·1.5252+ 16.8·1.525 – 12.2 = – 0.0105.
Так как произведение f (1.5) f (x 2) больше нуля, то в качестве нового отрезка локализации принимается отрезок [1.525, 1.55]. Аналогично выполняются шаги c третьего по седьмой, дающие следующие значения приближения корня
x 3= 1.5375 – центр отрезка [1.525, 1.55],
x 4= 1.53125 – центр отрезка [1.525, 1.5375],
x 5= 1.53438 – центр отрезка [1.53125, 1.5375],
x 6= 1.53281 – центр отрезка [1.53125, 1.53438],
x 7= 1.53203 – центр отрезка [1.53125, 1.53281].
Значение относительной погрешности вычисления приближения x 7= 1.53203 корня уравнения будет определяться по формуле
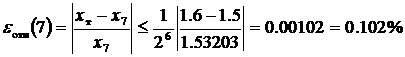 .
.
Эта величина совпадает с длиной отрезка локализации найденного приближения корня, отнесённой к величине этого приближения
 .
.
Таким образом, если в задаче требовалось бы вычислить значение корня с относительной погрешностью ε отн= 0.002, то уточнение значения корня можно прекратить.
Метод хорд
Идея метода состоит в замене функции f (x) внутри отрезка [ a, b ]линейной функцией (см. рис.7). Точка пересечения x 1графика линейной функции и оси абсцисс принимается за значение одной из границ нового отрезка локализации корня, который выбирается так, чтобы выполнялось одно из условий
f (a) f (x 1) < 0 или f (x 1) f (b) < 0.
Далее процесс повторяется и находится следующее приближение корня x 2 – точка пересечения графика линейной функции нового отрезка с осью абсцисс.
 Для расчёта на каждом шаге абсциссы точки пересечения графика линейной функции и оси 0 x используются выражения вида
Для расчёта на каждом шаге абсциссы точки пересечения графика линейной функции и оси 0 x используются выражения вида
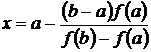 или
или  .
.
Процесс поиска корня продолжается до тех пор, пока не будет выполнено одно из условий окончания вычислений
 или
или  ,
,
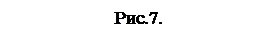 где δ абс и δ отн – задаваемые абсолютная и относительная разницы между соседними значениями приближения корня, соответственно. Абсолютная погрешность найденного значения корня может быть оценена с помощью неравенства
где δ абс и δ отн – задаваемые абсолютная и относительная разницы между соседними значениями приближения корня, соответственно. Абсолютная погрешность найденного значения корня может быть оценена с помощью неравенства
 ,
,
где
 ,
,  .
.
При решении практических задач, учитывая предположение о монотонности функции f (x) и её первой производной на отрезке [ a, b ] локализации корня, вместо приведённых формул для M и m используют их приближённые аналоги
 ,
,  .
.
Каждый из рассмотренных методов имеет свои достоинства и недостатки. В частности, итерационные методы обладают бóльшей скоростью сходимости вычислений, чем методы сужения интервала. Однако они требуют предварительных аналитических преобразований, что не всегда целесообразно.
Программное обеспечение. Для вычисления на заданном интервале корня уравнения, левая часть которого представляет собой вещественную функцию, в состав библиотеки IMSL включён модуль Zbren. Он реализует комбинацию методов половинного деления, хорд и обратной квадратичной интерполяции и оформлен в виде подпрограммы
Subroutine Zbren(F,errAbs,errRel,a,b,maxFn).
В качестве формальных параметров в подпрограмме используются:
F - имя внешней подпрограммы-функции (Real*4), в которой вычисляются значения функции f (x);
errAbs - первый критерий завершения вычислений (Real*4). Корень x принимается, если | f (x)|<errAbs. Можно задать errAbs=0;
errRel - желаемая относительная погрешность (Real*4). Корень принимается, если относительная разность между двумя последовательно полученными приближениями меньше errRel;
a и b - левая и правая границы отрезка локализации искомого корня (Real*4). На выходе a и b отличаются от начальных значений, причем b содержит приближенное значение корня;
maxFn - задает на входе в подпрограмму максимально допустимое количество вычислений функции f (x), а на выходе содержит число выполненных к ней обращений (Integer*4).
Если за заданное допустимое количество обращений к функции требуемая точность не достигается, то работа программы прекращается и выдается сообщение вида:
*** FATAL ERROR 1 from ZBREN. Failure to converge in
MAXFN = 10 function*** evaluations.
Для аргументов двойной точности (Real*8) используется подпрограмма с именем DZbren.
В качестве исходного материала для выполнения заданий лабораторной работы предложены относительно простые тексты программ, реализующих следующие методы:
- метод простой итерации
Subroutine Iter(eps,km,kp,Fi,x,*);
- метод Ньютона
Subroutine Newton(eps,km,kp,F,dF,x,*);
- метод хорд Subroutine Horda(a,b,eps,kp,F,x);
- метод половинного деления
Subroutine Polov(a,b,eps,kp,F,x).
В качестве формальных параметров в подпрограммах используются:
a и b - левая и правая границы отрезка локализации искомого корня (Real*4);
eps - относительная погрешность вычисления корня уравнения для метода половинного деления или относительная разница между соседними значениями приближения корня для прочих методов (Real*4);
km - предельное количество итераций (Integer*4). Параметр, обеспечивающий аварийный выход из подпрограммы при расходящемся итерационном процессе;
kp - номер канала вывода пошаговой печати (Integer*4). Для отключения печати устанавливать kp = 0;
Fi и F - имена внешних подпрограмм-функций (Real*4), в которых вычисляются значения функций j (x)и f (x), соответственно;
dF - имя подпрограммы-функции, в которой вычисляется значение первой производной функции f (x). Подпрограмма оформляется так же, как и подпрограмма F (Real*4);
x - вычисленное значение корня уравнения (Real*4). Для метода Ньютона и метода простой итерации это еще и входной параметр. Через него передается начальное приближение корня;
* - номер метки оператора, которому необходимо передать управление, если исходное уравнение неразрешимо данной подпрограммой. Метку задавать в форме - *<метка>, например, *25.
Подпрограммы Fi, F, dF оформляются в виде
Function F(x)
F =........
Return
End
Для выполнения первого этапа решения уравнения (отделения корней) посредством построения графика функции y = f (x) могут быть использована функция plot математической системы MATLAB.
Пример выполнения задания. Найти все корни уравнения
x 3– 7.3 x 2 + 16.8 x – 12.2 = 0,
лежащие на отрезке[1,4], с относительной погрешностью или относительной разницей между соседними значениями приближения корня 0.00001.
Решение. Для локализации корней уравнения на заданном отрезке применяется следующая программа, строящая график функции на экране монитора по 101-й точке:
Character*28 Nt
Real*4 Xm(101), Ym(101)
a = 1.
b = 4.
Nt = 'График функции по 101 точке.'
Do i = 1, 101
x = a + (b-a)*(i-1)/100
Xm(i) = a + (b-a)*(i-1)/100
Ym(i) = x**3-7.3*x**2+16.8*x-12.2
Enddo
Call Graf_1(101, Xm, Ym, 'x', 'y', Nt, 28)
Stop
End
При разработке этой программы в среде Visual Fortran необходимо создавать проект со стандартной графикой.
График функции, полученный на экране монитора, представлен на рис.8.

Рис.8.
Используя полученный график функции, можно найти приближенные значения корней уравнения: x 1» 1.5; x 2» 2.3; x 3» 3.5. Для уточнения значения первого корня будет применяться метод итераций, для второго – метод Ньютона, а для третьего – метод половинного деления. При применении метода итераций и метода Ньютона эти приближённые значения корней следует использовать как начальные приближения, а для метода половинного деления следует принять отрезок локализации третьего корня в виде [3.4, 3.6].
Основываясь на приведённом выше описании метода итераций, исходное уравнение следует привести к виду x = j (x). Для этого исходное уравнение надо записать в виде
x = x + λ (x 3– 7.3 x 2+ 16.8 x – 12.2),
при этом функция j (x) будет иметь вид
j (x) = x + λ (x 3– 7.3 x 2+ 16.8 x – 12.2),
а её производная
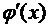 = 1+ λ (3 x 2 – 14.6 x + 16.8).
= 1+ λ (3 x 2 – 14.6 x + 16.8).
Учитывая, что для сходимости метода требуется выполнение условия  , для x 0 = 1.5 (см. пример в описании метода итераций) параметр λ следует принять равным –0.6. Таким образом, в подпрограмме Iter для уточнения корня должна быть использована следующая функция j (x):
, для x 0 = 1.5 (см. пример в описании метода итераций) параметр λ следует принять равным –0.6. Таким образом, в подпрограмме Iter для уточнения корня должна быть использована следующая функция j (x):
j (x) = x – 0.6(x 3– 7.3 x 2+ 16.8 x – 12.2).
Для реализации метода Ньютона необходимо знание первой производной функции
f (x) = x 3– 7.3 x 2+ 16.8 x – 12.2,
образующей рассматриваемое алгебраическое уравнение. Она имеет вид
 = 3 x 2– 14.6 x + 16.8.
= 3 x 2– 14.6 x + 16.8.
Подпрограмма Polov не требует каких-либо предварительных аналитических преобразований, для её работы достаточно описание только функции f (x).
Исходя из вышесказанного, программа уточнения корней заданного уравнения будет иметь вид:
External Fi, F, dF
Open(2, file='res_2.txt')
x_1 = 1.5
Call Iter(0.00001,10,2,Fi,x_1,*20)
x_2 = 2.3
Call Newton(0.00001,10,2,F,dF,x_2,*20)
Call Polov(3.4,3.6,0.00001,2,F,x_3)
Go to 40
20 Write(*,30)
Write(2,30)
30 Format(' *** Авария!!! Процесс расходится. ***')
40 Close(2)
Stop
End
Function F(x)
F = x**3-7.3*x**2+16.8*x-12.2
Return
End
Function Fi(x)
Fi = x-0.6*(x**3-7.3*x**2+16.8*x-12.2)
Return
End
Function dF(x)
dF = 3*x**2-14.6*x+16.8
Return
End
Программа вводится в память ЭВМ, отлаживается и выполняется. Ниже приведены результаты её работы, содержащиеся в файле res_2.txt:
Последовательность поиска
(метод простой итерации)
Итерация Значение аргумента
0 1.5000000
1 1.5300010
2 1.5317970
3 1.5319980
Последовательность поиска
(метод Ньютона)
Итерация Значение аргумента
1 2.2890080
2 2.2889530
3 2.2889530
Последовательность поиска
(метод половинного деления)
Итерация Значение аргумента
1 3.5000000
2 3.4500000
3 3.4750000
4 3.4875000
5 3.4812500
6 3.4781250
7 3.4796870
8 3.4789060
9 3.4792970
10 3.4791010
11 3.4790040
12 3.4790530
13 3.4790280
Результаты расчётов должны быть дополнены оценками погрешности определения значений корней уравнения.
Глава 3. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Численные методы решения систем линейных алгебраических уравнений
 ,
,
записываемых в матричной форме в виде
 ,
,
где
 ,
,
делятся на точные и итерационные. Они используются для систем, у которых количество неизвестных равно количеству уравнений и матрица A - не вырождена (её определитель не равен нулю). Точными методами условно называют методы, которые дают решение задачи посредством конечного числа арифметических операций. Итерационные методы позволяют получить решение системы как предел бесконечной последовательности его приближений. При применении итерационных методов существенным вопросом является вопрос об их сходимости.
Точные методы, к которым относятся метод Гауссаи его разновидности, не имеют дополнительных ограничений на свойства матрицы системы.
Метод Гаусса (K.F.Gauβ, 1849)
В основе метода Гаусса лежит идея последовательного исключения неизвестных, приводящая исходную систему с квадратной матрицей к легко разрешимой системе с верхней треугольной матрицей
 .
.
Данное преобразование может быть осуществлено многими способами. Однако все они основаны на свойстве систем, которое заключается в неизменности их решений при умножении любого уравнения на отличную от нуля постоянную или его замене на сумму с любым другим уравнением.
Один из простейших способов исключения состоит в следующем. Первое уравнение системы
 ,
,
которое на этом шаге считается ведущим, нормируется – делится на значение диагонального элемента a 11

или
 ,
,
где
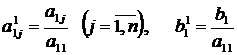 .
.
Если в исходной системе a 11 = 0, то в качестве первого уравнения следует взять любое другое с ненулевым первым коэффициентом, поменяв их местами. Полученное уравнение умножается на первый коэффициент второго уравнения a 21 и вычитается из него. В результате во втором уравнении пропадает слагаемое a 21 x 1, содержащее первое неизвестное x 1. Такие же операции проводятся со всеми последующими уравнениями. В результате система уравнений принимает вид
 .
.
Далее процесс повторяется. За ведущее берется второе уравнение и исключается неизвестное x 2 из всех уравнений, начиная с третьего
 .
.
Таким образом, за n шагов система уравнений последовательно сводится к треугольному виду, при этом для последнего уравнения выполняется только операция нормирования:
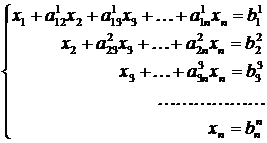 .
.
Полученная система с верхней треугольной матрицей может быть легко разрешена относительно неизвестных. Последнее уравнение системы определяет значение x n, что позволяет определить x n -1из предпоследнего уравнения как
 .
.
Выполняя аналогичные подстановки найденных неизвестных в вышестоящие уравнения, удается определить все компоненты решения x n –2,..., x 2, x 1.
Метод Гаусса даёт точное решение, если все исходные данные точны и все вычисления производятся точно. На практике, при выполнении вычислений, неизбежно проводятся округления. Ошибка округлений вносит погрешность в решение метода Гаусса. Таким образом, при операциях с округленными десятичными числами метод Гаусса даёт не точное решение x т системы линейных алгебраических уравнений, а некоторое приближенное решение  , где
, где
 ,
,  .
.
Степень отличия приближённого решения от точного определяется длиной разрядной сетки ЭВМ: чем больше разрядов в ней учитывается, тем это отличие меньше.
При определении погрешности вектора решения необходимо учитывать, что его компоненты в общем случае могут иметь разную погрешность. В силу этого погрешность решения принято оценивать по его норме
 или
или  или
или
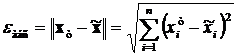 ,
,
где двойные модульные скобки  обозначают норму вектора.
обозначают норму вектора.
Для определения величины погрешности полученного решения  на практике используют следующий алгоритм вычисления её главной части. Сначала по имеющемуся решению пересчитывается вектор правых частей системы
на практике используют следующий алгоритм вычисления её главной части. Сначала по имеющемуся решению пересчитывается вектор правых частей системы
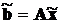 ,
,
а затем посредством повторного решения системы уравнений

находится вектор погрешностей  . С его помощью определяется как реальная абсолютная погрешность полученного решения
. С его помощью определяется как реальная абсолютная погрешность полученного решения
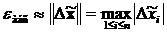 или
или 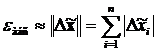 или
или  ,
,
так и его относительная погрешность
 .
.
Величина погрешности решения системы уравнений, получаемого методом Гаусса, зависит от двух основных факторов. Первый из них, как это было сказано выше – длина разрядной сетки, используемой в процессе вычислений, а второй – обусловленность матрицы системы. Обусловленность матрицы можно рассматривать как степень её чувствительности к накоплению ошибок округления в процессе преобразований. Снижение величины погрешности решения может быть достигнуто увеличением длины разрядной сетки. Повлиять на величину погрешности посредством изменения степени обусловленности матрицы системы невозможно, так как она является одной из её характеристик и изменение степени обусловленности матрицы требует изменения самой матрицы.
Метод Гаусса с выбором главного элемента
Основное накопление погрешностей решения в методе Гаусса происходит на этапе приведения системы к треугольному виду. Механизм накопления основной части этой погрешности заключается в привнесении погрешностей вычисления коэффициентов ведущего уравнения в коэффициенты последующих уравнений при исключении каждого очередного неизвестного. Анализ соотношений метода Гаусса показывает, что погрешности вычисления коэффициентов ведущего уравнения привносятся в соответствующие коэффициенты всех последующих уравнений в долях отношений этих коэффициентов к диагональному (главному) коэффициенту ведущего. В связи с этим привносимая погрешность будет тем меньше, чем меньше доли этих отношений. Поэтому в методе Гаусса с выбором главного элемента на каждом шаге исключения i -го неизвестного в качестве ведущего используетсяуравнение (с i -го по n -ое), содержащее максимальный по модулю коэффициент – главныйэлемент. При этом в качестве него может использоваться один из коэффициентов i -го столбца, i -ой строки или всей непреобразованной части матрицы. Первый подход называется выбором главного элементапостолбцу, второй – по строке, а третий – по всейматрице. При использовании двух последних происходит перестановка столбцов матрицы системы. Это приводит к изменению порядка следования компонент вектора неизвестных и требует его восстановления по окончании процесса решения.
В качестве примера применения метода Гаусса можно рассмотреть задачу отыскания решения следующей системы уравнений

при ограничении разрядной сетки вычислений до трёх знаков и с оценкой погрешности получаемого решения.
Поставленная задача будет решаться методом Гаусса с выбором главного элемента по столбцу.
1. Прямой ход.
а. Выбор главного элемента среди элементов первого столбца
 .
.
б. Нормировка первого уравнения
 .
.
в. Исключение элементов первого столбца
 .
.
г. Выбор главного элемента среди элементов второго столбца второго и третьего уравнений
 .
.
д. Нормировка второго уравнения
 .
.
е. Исключение элементов второго столбца
 .
.
ё. Нормировка последнего уравнения
 .
.
2. Обратный ход
 ,
,
 .
.
В итоге получено решение системы уравнений
 .
.
3. Погрешность найденного решения.
а. Пересчёт вектора правых частей системы
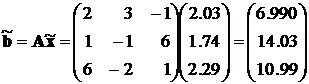
б. Формирование системы уравнений, определяющей погрешности решения
 ,
,
то есть

в. Решение системы относительно погрешностей оно выполняется аналогично пунктам 1 и 2. Прямой ход (пункт 1) даёт следующую систему с верхней треугольной матрицей
 ,
,
а обратный ход позволяет получить решение
 .
.
г. Оценка абсолютной и относительной погрешностей решения системы линейных алгебраических уравнений
 ,
,
 ,
,
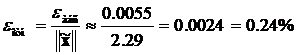 .
.
Итерационные методы. К этим методам относятся метод простых итераций, метод Зейделя и ряд других. Методы этой группы обладают высокой эффективностью, но их применение связано с рядом ограничений, накладываемых на свойства матрицы A.
Метод простых итераций
Метод основывается на приведении исходной системы  к форме
к форме  , где D – квадратная матрица, полученная из матрицы A, а p – вектор-столбец, полученный из b. Это преобразованиеможет быть выполнено многими способами. Например, путем разрешения i -го уравнения относительно i -го неизвестного для каждого i:
, где D – квадратная матрица, полученная из матрицы A, а p – вектор-столбец, полученный из b. Это преобразованиеможет быть выполнено многими способами. Например, путем разрешения i -го уравнения относительно i -го неизвестного для каждого i:
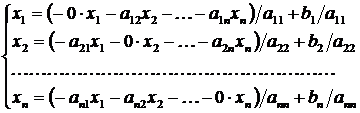
при этом элементы матрицы D и вектора p

будут вычисляться следующим образом
 .
.
Далее процесс уточнения корня строится по итерационной схеме
 ,
,
 ,
,
………………
 ,
,
……………….
где x 0 – начальное приближение вектора решения системы. То есть
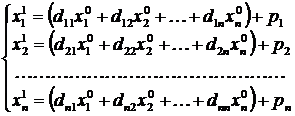 ,
,

и так далее.
Если последовательность векторов x k (k = 0,1,2,...) имеет конечный предел (тоже вектор), то итерационный процесс сходится к точному решению системы x т за бесконечно большое число шагов. Абсолютная и относительная погрешности найденного вектора решения системы уравнений на k -ом шаге (x k) могут быть получены из выражений
 ,
, 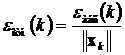 ,
,
где в качестве нормы матрицы D можно использовать любое из трёх соотношений
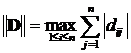 ,
,  ,
, 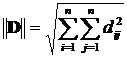 .
.
Кроме приведённого выражения для абсолютной погрешности существуют другие формы её записи
 ,
,  .
.
Формулы для вычисления погрешности вектора решения системы линейных алгебраических уравнений требуют нахождения нормы матрицы системы, поэтому на практике часто итерации завершают при выполнении одного из условий
 или
или 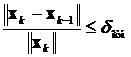 ,
,
где δ абс и δ отн – задаваемые абсолютная и относительная разницы между соседними приближениями вектора решения, соответственно. В этом случае надо помнить, что истинная погрешность определения решения может заметно отличаться от δ абс или δ отн. Поэтому после завершения поиска решения необходимо вычислить истинное значение его погрешности по приведённым выше формулам для ε абс или ε отн.
Встречаются ситуации, когда последовательность вычисляемых векторов x k (k = 0,1,2,...) не имеет предела. В этом случае метод расходится, и описанная итерационная схема не может быть применена для решения системы уравнений. Для того, чтобы последовательностьвекторов x k (k = 0,1,2,...) при любом начальном векторе x 0 сходилась к точному решению системы, надо выбрать матрицу D так, чтобы её норма  была меньше единицы.
была меньше единицы.
Если описанный выше приём формирования итерационной схемы не позволяет получить матрицу D, которая подчиняется условию сходимости, а матрица А – симметрична и положительно определена, то можно поступить следующим образом. Исходная система линейных алгебраических уравнений

приводится к эквивалентному виду

путем переноса произведения Ax в правую часть уравнения, умножения обеих частей уравнения на константу a и добавления к ним вектора x. В результате этого преобразования получается итерационная схема
 ,
,
где
 .
.
Здесь под матрицей E понимается единичная матрица, а параметр a k вычисляется с использованием выражения
 ,
,
где
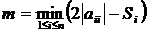 ,
,  ,
,  .
.
Подбирая таким способом коэффициент a k на каждом шаге процесса итераций, удается получить матрицы D k, подчиняющиеся условию сходимости. Описанный приём называется методом простых итераций с релаксацией.
Если система уравнений

имеет матрицу A, которая не является симметричной и положительно определённой, то надо произвести её симметризацию. Она заключается в умножении левой и правой частей системы на транспонированную матрицу A T
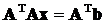 ,
,
что приводит исходную систему к системе
 ,
,
где
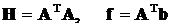 ,
,
в которой матрица H симметрична и положительна определена.
Метод Зейделя (L.Seidel, 1874)
Этот метод является разновидностью метода простых итераций. Исходная система приводится к такому же виду, как и в методе простых итераций, но процесс итераций организуется иным образом. Как только на k -ой итерациивычислена i -я компонента  вектора x k, её значение используют для вычисления последующих компонент
вектора x k, её значение используют для вычисления последующих компонент  ,
,  ,...,
,...,  этого вектора, не дожидаясь начала следующей итерации. Например
этого вектора, не дожидаясь начала следующей итерации. Например
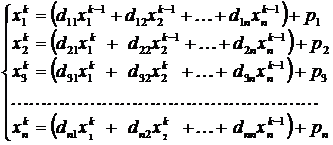 .
.
Вопрос о сходимости метода Зейделя, в общем виде, является открытым. Однако известно, что выполнение условия сходимости метода простых итераций гарантирует сходимость метода Зейделя. При этом благодаря особенностям итерационной схемы, метод Зейделя позволяет за то же количество шагов, что и метод простых итераций, получить более точный результат.
Если при решении системы уравнений методом Зейделя итерационный процесс расходится, то могут использоваться описанные выше приемы с релаксацией и симметризацией системы уравнений.
В качестве примера применения метода Зейделя можно рассмотреть задачу поиска решения следующей системы уравнений

с относительной разницей между соседними приближениями вектора решения не более 0.01 и с оценкой его погрешности.
Следуя алгоритму метода Зейделя, требуется преобразовать исходную систему уравнений к виду
 ,
,
где
 ,
,
и выполнить её проверку на сходимость

Так как условие сходимости выполняется, то итерационный процесс может быть начат с любого удобного значения вектора x. В качестве начального приближения обычно принимается нулевой вектор
 .
.
Первая итерация


Вторая итерация
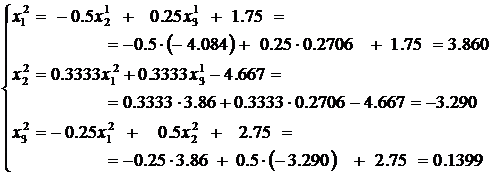

Третья итерация


Четвёртая и пятая итерации дают соответственно
 ,
,  ,
,
 ,
,  .
.
Определение погрешности решения по последней итерации
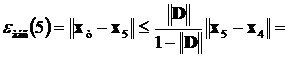
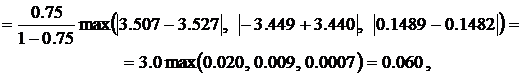
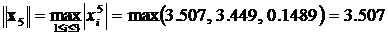 ,
,
.
Каждый из рассмотренных методов имеет свои достоинства и недостатки. В частности, метод Гаусса позволяет получить решение за конечное число шагов. Однако его методические ошибки, связанные с размером разрядной сетки вычислений, резко нарастают с увеличением порядка системы и не позволяют применять его для систем высоких порядков без использования специальных приёмов. Итерационные методы позволяют получать решение систем большего порядка, но требуют, чтобы матрица системы обладала определёнными свойствами, обеспечивающими их сходимость. Необходимо также отметить, что выполнение этих требований часто не гарантирует высокой скорости сходимости итерационных методов.
Программное обеспечение. Для решения систем линейных алгебраических уравнений общего вида методом Гаусса с выбором главного элемента в состав библиотеки IMSL включён модуль Lslrg
Subroutine Lslrg(n,A,Lda,B,Ipath,X).
В качестве формальных параметров в модуле используются:
n - порядок системы уравнений (Integer*4);
A - двумерный массив размерностью n´n, содержащий значения матрицы А системы уравнений (Real*4);
Lda - ведущий размер массива A – величина, использованная при задании размерности массива A(Lda,Lda), Lda ³ n, причём обычно Lda = n (Integer*4);
B - одномерный массив размерностью n, содержащий значения вектора свободных членов b (Real*4);
Ipath - признак, определяющий вид решаемой системы: если решается система Ax = b, то Ipath = 1, если решается система A T x = b, то Ipath = 2 (Integer*4);
X - одномерный массив размерностью n, возвращающий найденное значение вектора неизвестных x (Real*4).
Для аргументов двойной точности (Real*8) используется подпрограмма с именем DLslrg.
Аварийные ситуации с прерыванием работы программы возникают в случае, если матрица системы уравнений является плохо обусловленной или вырожденной. В этом случае следует использовать подпрограмму Lsarg (DLsarg для двойной точности аргументов), в которой осуществляется итерационное уточнение решения. Формальные параметры этих подпрограмм те же, что у подпрограмм Lslrg и DLslrg.
В качестве исходного материала для выполнения заданий лабораторной работы предложены относительно простые тексты программ, реализующих следующие методы:
- метод Гаусса
Subroutine Gauss(n,A,B,X,*);
- метод Гаусса с выбором главного элемента по всей матрице
Subroutine Gauss_G(n,A,B,X,*);
- метод итераций
Subroutine Su_It(n,A,B,eps,km,kp,X,ki,*);
- метод итераций с релаксацией и симметризацией
Subroutine Su_It_RS(n,A,B,eps,km,kp,X,ki,*);
- метод Зейделя
Subroutine Seidel(n,A,B,eps,km,kp,X,ki,*);
- метод Зейделя с релаксацией и симметризацией
Subroutine Seid_RS(n,A,B,eps,km,kp,X,ki,*).
В качестве формальных параметров здесь используются:
n - порядок системы уравнений (Integer*4);
A - двумерный массив размерностью n´n, содержащий значения матрицы А системы уравнений (Real*4);
B - одномерный массив размерностью n, содержащий значения вектора свободных членов b (Real*4);
X - одномерный массив размерностью n, возвращающий найденное значение вектора неизвестных x (Real*4);
eps - величина относительной погрешности вычислений (Real*4);
km - предельное количество итераций (Integer*4). Параметр, обеспечивающий аварийный выход из подпрограммы при расходящемся итерационном процессе;
kp - номер канала вывода на печать результатов промежуточных итераций (Integer*4). При kp=0 печать отсутствует;
ki - количество итераций, за которое было получено решение с заданной погрешностью (Integer*4);
* - номер метки оператора, которому необходимо передать управление, если исходная система уравнений неразрешима.
При использовании подпрограмм Gauss и Gauss_G следует помнить, что возвращаемые значения элементов массива B и элементов массива A, расположенных выше главной диагонали, соответствуют преобразованной системе линейных алгебраических уравнений с верхней треугольной матрицей.
Пример выполнения задания. Решить заданную ниже систему линейных алгебраических уравнений с использованием метода Гаусса с выбором главного элемента
 .
.
В программе предусмотреть режим её аварийного завершения при отсутствии решения системы уравнений с выводом комментирующего ситуацию сообщения.
Решение. Решение поставленной задачи представлено в виде приведённой ниже программы
Real*4 A(10,10), B(10), X(10)
Open(1, file='dat_3.txt')
Open(2, file='res_3.txt')
Read(1,1) ((A(i,j), j=1,10), B(i), i=1,10)
1 Format(/(10F5.1,F6.1))
Write(2,2) ((A(i,j), j=1,10), B(i), i=1,10)
2 Format(22x,'Матрица А',19x, 'Вектор В'/(10F5.1,F6.1))
Call Gauss_G(10, A, B, X, *16)
Write(2,14) (X(i), i=1,10)
14 Format(/11x,'Метод Гаусса с выб.гл.эл.:'
* ' вектор решения Х '/(5F12.7))
Go to 20
16 Write(*,18)
Write(2,18)
18 Format(/' *** Метод Гаусса с выб.гл.эл.:',
* ' система не имеет решения!!! ***')
20 Close(1)
Close(2)
End
Программа вводится в память ЭВМ и отлаживается. Исходные данные к программе подготавливаются в отдельном файле с именем dat_3.txt в следующем виде:
Матрица А Вектор В
6.0 2.0 1.0 1.0
2.0 6.0 2.0 1.0 2.0
1.0 2.0 6.0 2.0 1.0 2.0
1.0 2.0 6.0 2.0 1.0 2.0
1.0 2.0 6.0 2.0 1.0 2.0
1.0 2.0 6.0 2.0 1.0 2.0
1.0 2.0 6.0 2.0 1.0 2.0
1.0 2.0 6.0 2.0 1.0 2.0
1.0 2.0 6.0 2.0 2.0
1.0 2.0 6.0 1.0
Результаты работы программы, помещённые в файл с именем res_3.txt, приведены ниже
Матрица А Вектор В
6.0 2.0 1.0.0.0.0.0.0.0.0 1.0
2.0 6.0 2.0 1.0.0.0.0.0.0.0 2.0
1.0 2.0 6.0 2.0 1.0.0.0.0.0.0 2.0
.0 1.0 2.0 6.0 2.0 1.0.0.0.0.0 2.0
.0.0 1.0 2.0 6.0 2.0 1.0.0.0.0 2.0
.0.0.0 1.0 2.0 6.0 2.0 1.0.0.0 2.0
.0.0.0.0 1.0 2.0 6.0 2.0 1.0.0 2.0
.0.0.0.0.0 1.0 2.0 6.0 2.0 1.0 2.0
.0.0.0.0.0.0 1.0 2.0 6.0 2.0 2.0
.0.0.0.0.0.0.0 1.0 2.0 6.0 1.0
Метод Гаусса с выб.гл.эл.: вектор решения Х
.0617220.2318464.1659752.1535270.1716805
.1716805.1535270.1659751.2318464.0617220
Результаты подобных расчётов должны быть дополнены оценками погрешности найденного вектора решения системы линейных алгебраических уравнений, что целесообразно сделать в программе.






