Логические операции используются в алгоритмах на графах, например, при поиске путей в графе. При этом матрица смежности графа умножается сама на себя. Умножение проводится по правилам обычной алгебры с тем исключением, что операция суммы заменяется дизъюнкцией, а операция умножения – конъюнкцией. Тогда квадрат матрицы смежности представляет матрицу всех путей длиной 2, куб – длиной 3 и т.д. Рассмотрим пример (рис. 36).
Рис. 36. Ориентированный граф и его матрица смежности
Найдем все пути длиной 2:
Получили матрицу M2 всех путей в графе длиной 2. Процесс получения первой строки M2 подробно рассмотрен в табл. 22.
Таблица 22
Вычисление первой строки M2
| 0 | 1 | 0 | Первая строка М | ||
| Ù | Ù | Ù | Поразрядная конъюнкция | ||
| 0 | 1 | 1 | Первый столбец М | ||
| 0 | Ú | 1 | Ú | 0 | =1, т.е. имеется путь из x1bx1 по двум дугам: t1, t4 |
| Дизъюнкция результатов | |||||
ЭЛЕМЕНТАРНЫЕ ДВОИЧНЫЕ ПЕРЕКЛЮЧАТЕЛЬНЫЕ
ФУНКЦИИ И ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
СИСТЕМ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ
Элементарные переключательные функции одной переменной
Переключательные (логические) функции, соответствующие логическим операциям В2aВ, называют элементарными. Количество переключательных (логических) функций от n переменных определяется выражением 22n, поскольку |Bn|=2n, а на каждом из 2n наборов переключательная (логическая) функция может принимать одно из значений из того же множества В (табл. 23).
Таблица 23
Переключательные функции от n переменных
| № | Набор | Номер логической функции | |||||
| п/п | значений переменных | 0 | 1 | 2 | 3 | ... | 22n-1 |
| 1 | 00...00 | 0 | 1 | 0 | 1 | ... | 1 |
| 2 | 00...01 | 0 | 0 | 1 | 1 | ... | 1 |
| 3 | 00...10 | 0 | 0 | 0 | 0 | ... | 1 |
| 4 | 00...11 | 0 | 0 | 0 | 0 | ... | 1 |
| . . . | . . . | . . . | . . . | . . . | . . . | ... | . . . |
| 22 | 11...11 | 0 | 0 | 0 | 0 | ... | 1 |
Например, рассмотрим все переключательные (логические) функции одной переменной (табл. 24).
Таблица 24
Переключательные функции одной переменной
| Переключательная (логическая) функция | ||||
| х | f0(x) | f1(x) | f2(x) |  f3(x)
|
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
Поскольку 221=4, то имеется четыре логических функции одной переменной, две из них – константы: f0(x)=0, f3(x)=1 (f0(x) – константа нуля, f3(x) – константа единицы). Здесь номер функции означает десятичное число, соответствующее двоичному числу, записанному в соответствующем столбце табл. 24.
Функция f2(x)=х, т.е. совпадает со значением переменной. Эта функция называется функцией повторения. Функция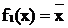 
нам уже известна – это инверсия.
Можно заметить, что для каждой функции одной переменной существует инверсная ей функция:
Элементарные переключательные (логические) функции
Двух переменных
Рассмотрим все функции двух переменных (табл. 25).
Таблица 25
Переключательные функции двух переменных
| 20 | 21 | 22 | 23 | ||||
| Набор | Название | Формула | |||||
| 20 | х1 | 0 | 1 | 0 | 1 | функции | |
| 21 | х2 | 0 | 0 | 1 | 1 | ||
| f0 | 0 | 0 | 0 | 0 | Константа 0 | 0 | |
| f1 | 1 | 0 | 0 | 0 | Функция Пирса (Вебба), «стрелка Пирса», ИЛИ-НЕ | х1¯х2=
| |
| f2 | 0 | 1 | 0 | 0 | Запрет х2 | 
| |
| f3 | 1 | 1 | 0 | 0 | Отрицание х2 | 
| |
| f4 | 0 | 0 | 1 | 0 | Запрет х1 | 
| |
| f5 | 1 | 0 | 1 | 0 | Отрицание х1 | 
| |
| f6 | 0 | 1 | 1 | 0 | Сложение (сумма) по mod2 | х1Åх2=
| |
| f7 | 1 | 1 | 1 | 0 | Функция Шеффера, «штрих Шеффера», И-НЕ | х1|х2=
| |
| f8 | 0 | 0 | 0 | 1 | Конъюнкция, И | х1х2 | |
| f9 | 1 | 0 | 0 | 1 | Эквиваленция (эквивалентность) | х1«х2=
| |
| f10 | 0 | 1 | 0 | 1 | Повторение х1 | х1 | |
| f11 | 1 | 1 | 0 | 1 | Импликация х2 в х1 | х2®х1
| |
| f12 | 0 | 0 | 1 | 1 | Повторение х2 | х2 | |
| f13 | 1 | 0 | 1 | 1 | Импликация х1 в х2 | х1®х2
| |
| f14 | 0 | 1 | 1 | 1 | Дизъюнкция, ИЛИ | х1Úх2 | |
| f15 | 1 | 1 | 1 | 1 | Константа 1 | 1 | |
Всего таких функций имеется 222=24=16. Есть функции, зависящие только от одной переменной. Есть функции, не зависящие от переменных, – константы 0, 1. Такие функции называют вырожденными:
f3(x1x2)= 
; f5(x1x2)= 
; f10(x1x2)=х1; f12(x1x2)=х2;
f0(x1x2)=0; f15(x1x2)=1.
Некоторые функции мы тоже уже знаем: конъюнкцию f8(x1x2)=х1х2 (точку между х1 и х2 опускаем); эквиваленцию (эквивалентность) f9(x1x2)=х1«х2=х1х2Ú 
(здесь эквиваленция представлена в виде дизъюнкции двух конъюнкций, что можно доказать, составив таблицу истинности); импликацию f11(x1x2)=х2®х1= Úх1, f13(x1x2)=х1®х2= 
Úх2; дизъюнкцию f14(x1x2)=х1Úх2.
Кроме этого, имеются другие функции, зависящие от двух переменных: f1(x1x2)= 
– функция Пирса (Вебба) («стрелка Пирса»); f2(x1x2)= 
– запрет х2; f4(x1x2)= 
– запрет х1; f6(x1x2)=x1Åx2 –сложение по модулю 2 (функция, инверсная эквиваленции); f7(x1x2)= 
– функция Шеффера («штрих Шеффера»).
