Формулы ПФ f1 и f2 равносильны, если их эквиваленция f1«f2 является тождественно истинной (тавтологией). Равносильность, как правило, обозначается º, но мы будем «нестрого» использовать в дальнейшем и простое равенство =.
Равносильность – это некоторое отношение, которое обладает следующими свойствами:
а) оно рефлексивно, т.е. fºf, всякая формула f равносильна самой себе;
б) оно симметрично: если f1ºf2, то f2ºf1;
в) оно транзитивно: если f1ºf2 и f2ºf3, то f1ºf3.
Равносильности формул алгебры логики часто называют законами. Они подобны законам алгебры множеств. Говорят, что булева алгебра логических (переключательных) функций изоморфна булевой алгебре множеств.
Законы булевой алгебры:
1) хºх – закон тождества. Закон тождества означает, что мысль, заключенная в некотором высказывании, соответствующем двоичной переключательной функции остается (считается) неизменной на протяжении всего рассуждения.
2) 
– закон противоречия. Закон противоречия гласит, что никакое предложение не может быть истинным одновременно со своим отрицанием.
3) 
– закон исключенного третьего. Закон исключенного третьего говорит о том, что для каждого высказывания имеется лишь две возможности: быть либо истинным, либо ложным. Третьего не дано.
4) 
– закон двойного отрицания.
5) х×хºх; хÚхºх – закон идемпотентности (от латинского idem – то же, potentio – сила). Этот закон рассматривается относительно операций конъюнкции и дизъюнкции. В силу закона идемпотентности в алгебре логики, как и в алгебре множеств, нет показателей степеней, коэффициентов. Оказывается, основные законы алгебры логики двойственны (справедливы относительно конъюнкции и дизъюнкции).
6) х×yºy×х; xÚyºyÚх – закон коммутативности (переместительности).
7) х×(y×z)º(x×y)×z; xÚ(yÚz)º(xÚy)Úz – закон ассоциативности (сочетательности).
8) х×(yÚz)ºxyÚхz; xÚyz)º(xÚy)Ú(хÚz) – закон дистрибутивности (распределительности). Закон дистрибутивности относительно дизъюнкции не имеет аналога в обычной алгебре.
9) 
; 
закон Де Моргана. Отрицание конъюнкции высказываний равносильно дизъюнкции отрицаний этих высказываний. Отрицание дизъюнкции высказываний равносильно конъюнкции отрицаний этих высказываний.
10) xÚхyºх; х(xÚy)ºх – закон поглощения. Короткий член конъюнкции (дизъюнкции) поглощает длинный член, содержащий короткий в качестве составной части.
11) 
– закон склеивания. Здесь склеивание производится по переменной y; она исключается, если входит в члены дизъюнкции (конъюнкции) с разными знаками, а остальные элементы в конъюнкции (дизъюнкции) с ней одинаковы.
12) 
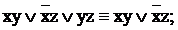
– закон обобщенного склеивания, т.е. в дизъюнкции конъюнкций «лишней» является конъюнкция, полученная в результате конъюнкции членов перед инверсной и неинверсной переменной в двух других конъюнкциях. То же можно сказать и о конъюнкции дизъюнкций, в которых имеются дизъюнкции с такими переменными.
Еще раз отметим двойственность законов алгебры логики: они действуют как относительно дизъюнкции, так и относительно конъюнкции.
Кроме перечисленных законов, которые можно доказать, например, построив соответствующие таблицы истинности (соответствия), большое значение имеют так называемые соотношения 0 и 1, полученные на основании законов алгебры логики:
причем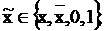 
два последних соотношения – это закон исключенного третьего и закон противоречия. Так, например:
1Ú0=1; 1×0=0;
0Ú1=1; 0×1=0.
Здесь мы стали применять простое равенство (=).
Рассмотренные законы применимы не только к отдельным переменным, но и к группам переменных, объединенных операциями алгебры логики, т.е. х, например, может быть в свою очередь конъюнкцией 
а 
.
В алгебре переключательных функций установлен порядок выполнения действий. При отсутствии в выражении скобок первыми выполняются операции отрицания (инверсии), затем операции конъюнкции и последними – дизъюнкции.
При наличии в выражении скобок в первую очередь выполняются операции внутри скобок.
