Если граф имеет ребра неединичной длины, то подобное присвоение индексов должно учитывать их длину, причем индексы эти могут уменьшаться в ходе разметки вершин с учетом индексов всех соседних вершин [18]. Оптимальный путь ищут, двигаясь из начальной вершины в сторону тех вершин, индекс которых равен индексу текущей минус длина ребра. Может быть, таких оптимальных (кратчайших) путей будет и не один, но все они имеют длину, равную индексу начальной вершины после завершения разметки.
ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ И СПОСОБЫ ИХ ЗАДАНИЯ
Понятие о переключательных функциях
Функция, принимающая значение из множества {0,1,¼,k-1}, аргументы которой принимают значения из этого же множества, называется переключательной функцией (ПФ) или функцией k-значной логики [9].
Это может быть тернарное множество T={0,1,2}, или множество Q={0,1,2,3}или другое k-элементное множество.
Такая функция может быть задана таблицей из kn строк, где n – количество аргументов. Например, переключательная функция для n=2 (переменные a, b) и k=3 представлена в табл. 7.
Таблица 7
Некоторая трехзначная переключательная функция
двух переменных
| а | b | f(ab) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 2 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| 1 | 2 | 1 |
| 2 | 0 | 2 |
| 2 | 1 | 2 |
| 2 | 2 | 2 |
В табл. 7 число строк равно числу размещений с повторениями из тернарного множества по двум местам. Подобные таблицы называются таблицами истинности или соответствия.
Получим номер ПФ в троичной системе счисления: 222111000. Здесь каждый разряд – соответствует степени числа 3: 322, 321, 320, 312, 311, 310, 32, 31, 30. При этом 22, 21, 20, 12, 11, 10, 2, 1, 0 – троичные числа, соответствующие значениям переменных a, b.
Можно получить номер ПФ в десятичной системе счисления:
Здесь степени числа три – 8, 7, 6, 5, 4, 3, 2, 1, 0.
Если различных двухзначных ПФ 
, то число различных k-значных ПФ равно 
.
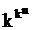Выделяется ряд различных элементарных функций [9]:
1) 
– конъюнкция;
2) 
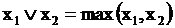– дизъюнкция; 
3) 
– сумма по модулю k – остаток от деления суммы x1+x2 на k;
4) 
– цикл – циклический сдвиг значений;
5) константы 0,1,2,...,k-1.
Одноместные функции имеют вид 
, где 
– показатель значения переменной: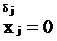 
, если 
, иначе 
.
Часто таблицы переключательных функций представляют для компактности, как показано в табл. 8-10.
Таблица 8
Трехзначная ПФ «дизъюнкция a,b»
| b | |||
| a | 0 | 1 | 2 |
| 0 | 0 | 1 | 2 |
| 1 | 1 | 1 | 2 |
| 2 | 2 | 2 | 2 |
Таблица 9
Трехзначная ПФ «сумма a,b по модулю 3»
| b | |||
| a | 0 | 1 | 2 |
| 0 | 0 | 1 | 2 |
| 1 | 1 | 2 | 0 |
| 2 | 2 | 0 | 1 |
Таблица 10
Трехзначная ПФ «a плюс 1 по модулю 3 – циклический сдвиг a»
| a | (a+1)mod3 |
| 0 | 1 |
| 1 | 2 |
| 2 | 0 |
Функция переключательного типа может быть проиллюстрирована блоком «решение» в схемах алгоритмов [11].
