Равносильные преобразования – это замена одной формулы другой, равносильной формулой. Если в равносильные формулы всюду вместо какой-нибудь переменной подставить одну и ту же формулу, то вновь полученные формулы также окажутся равносильными.
Под упрощением формулы будем понимать равносильные преобразования, приводящие к формуле, содержащей меньшее число переменных, чем исходная. Такие преобразования формул логики необходимы при синтезе, анализе, контроле дискретных устройств, а в последнее время – в системах искусственного интеллекта (логического вывода).
Мощным аппаратом для таких равносильных преобразований помимо рассмотренных законов алгебры логики являются так называемые основные формулы равносильных преобразований, полученные с использованием этих законов [34].
Пусть 
– некоторая переменная, причем символ ~ означает, что неважно, инверсная они или нет, т.е. 
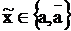; тогда 
.
Пусть 
– некоторая функция, зависящая как от переменной х и ее инверсии 
, так и от других переменных 
. Под одноименностью будем понимать и соответствие знаков инверсии (т.е. одновременное наличие или отсутствие). Тогда, если переменная 
находится в конъюнкции с некоторой функцией, зависящей от данной переменной и от других переменных, то в этой функции все одноименные переменные заменяются на константу 1, а все переменные , инверсные одноименной, – на константу 0. Сама же переменная перед функцией остается без изменения. Таким образом:
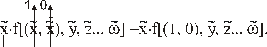
Такая запись означает, что:
Условно замену переменных на константу в функции f обозначаем стрелками.
Примеры.
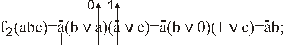
Для облегчения запоминания рекомендуется мнемоническое правило [34]. Представим формулу равносильного преобразования относительно конъюнкции из вида переключательной схемы, в которой конъюнкции 
и функции f соответствует их последовательное соединение. Такое соединение напоминает символ 1 (рис. 39). Для простоты на рис. 1 не указаны переменные функции f. Это значит, что одноименные переменные в f заменяются на константу 1. Соответственно переменные 
в f заменяются на константу 0.
Рис. 39. Иллюстрация мнемонического правила для формулы равносильных преобразований относительно конъюнкции
Рассмотрим формулу равносильных преобразований относительно дизъюнкции. Если переменная находится в дизъюнкции с функцией, зависящей от данной переменной и от других переменных, то в этой функции все одноименные переменные заменяются на константу 0, а все переменные 
, инверсные одноименной, заменяются на константу 1. Сама же переменная остается без изменения:
Это означает, что:
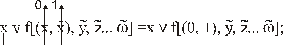
Примеры.
f(аbс)= 
В этой функции в явном виде нет отдельной переменной (), однако нетрудно заметить, что 
. Поэтому обозначим аb, например, х:
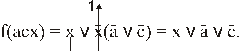
Отсюда:
Имеется соответствующее мнемоническое правило. Представим формулу равносильного преобразования относительно дизъюнкции в виде переключательной схемы, в которой дизъюнкции и функции f соответствует их параллельное соединение. Такое соединение напоминает символ 0 (рис. 40). Это значит, что одноименные переменные в f заменяются на константу 0. Соответственно переменные в f заменяются на константу 1.
Рис. 40. Иллюстрация мнемонического правила для формулы равносильных преобразований относительно дизъюнкции
Основные формулы равносильных преобразований можно доказать методом подстановки в них вместо переменной х ее возможных значений 0, 1 и сравнения правой и левой частей уравнения.
Докажем, например, формулу:
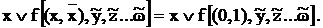
Пусть х=0; тогда левая часть формулы:
а правая:
т.е. равенство справедливо.
Пусть х=1; тогда левая часть формулы
а правая часть формулы
Равенство также справедливо, несмотря на отличия в функции f.
Аналогично доказывается формула для конъюнкции, например:
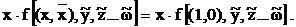
При х=0:
равенство справедливо, несмотря на отличия в функции f.
При х=1:
равенство также справедливо.
Основные формулы равносильных преобразований имеют следствия, которые позволяют разложить логическую функцию по любой переменной.
Следствие 1.
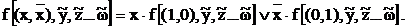
Следствие может быть доказано путем конъюнкции функции с тождественно истинной формулой 
и последующего применения формул равносильного преобразования:
.
Это известное разложение Шеннона.
Пример 1. Разложить логическую функцию по переменной b:
f(аbсd)=а 
Ú(
Úb)с[а Úd( Úb)]=
=b{а×0Ú( Ú1)с[а×0Úd( Ú1)]}Ú {а×1Ú( Ú0)×с[а×1Úd( Ú0)]}=
Следствие 2.
.
Доказательство:
f=fÚ0=fÚх×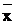 
=(fÚх)(fÚ )= 
.
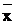Пример 2. Разложим ту же функцию f(авсd) (пример 1) по переменной а с помощью следствия 2:
f(аbсd)={аÚ0× Ú(1Úb)×с[0× Úd(1Úb)]}{ Ú1× Ú(0Úb)×с[1× Úd(0Úb)]}=
