Дано: двоичная переключательная функция (ПФ) №17410.
Получим соответствующий двоичный код: 101011102 (27+25+23+22+21). Таблица истинности ПФ №17410 показана в табл. 28.
Таблица 28
Таблица истинности
| переменные | ВС | f(abc) | |||
| а | b | с | |||
| 0 | 0 | 0 | 0 | 0 | 20 |
| 0 | 0 | 1 | 1 | 1 | 21 |
| 0 | 1 | 0 | 2 | 1 | 22 |
| 0 | 1 | 1 | 3 | 1 | 23 |
| 1 | 0 | 0 | 4 | 0 | 24 |
| 1 | 0 | 1 | 5 | 1 | 25 |
| 1 | 1 | 0 | 6 | 0 | 26 |
| 1 | 1 | 1 | 7 | 1 | 27 |
Получим восьмеричный код ПФ: 2568.
Получим шестнадцатеричный код ПФ: АЕ16.
Получим символическую форму: f(abc)10=1,2,3,5,7 [0,4,6].
В двоичном виде: f(abc)2=0012Ú0112Ú1012 Ú1112.
Определим свойства ПФ №17410.
1. Поскольку на наборе 000 ПФ равна 0, то ПФ обладает свойством сохранения константы «0».
2. Поскольку на наборе 111 ПФ равна 1, то ПФ обладает свойством сохранения константы «1».
3. Рассмотрим все возможные линейные ПФ от трех аргументов в зависимости от значений коэффициентов полинома  :
:
Таблица 29
Переключательные функции от трех аргументов
| Значение коэффициентов | Линейная функция | |||
| k0 | k1 | k2 | k3 | |
| 0 | 0 | 0 | 0 | ≡0 |
| 0 | 0 | 0 | 1 | a |
| 0 | 0 | 1 | 0 | b |
| 0 | 0 | 1 | 1 | a  b b
|
| 0 | 1 | 0 | 0 | c |
| 0 | 1 | 0 | 1 | c  a a
|
| 0 | 1 | 1 | 0 | c  b b
|
| 0 | 1 | 1 | 1 | c  b b  a a
|
| 1 | 0 | 0 | 0 | ≡1 |
| 1 | 0 | 0 | 1 |  =a =a  1 1
|
| 1 | 0 | 1 | 0 | b  1= 1= 
|
| 1 | 0 | 1 | 1 | a  b b  1= 1= 
|
| 1 | 1 | 0 | 0 | 1  c= c= 
|
| 1 | 1 | 0 | 1 | c  a a  1= 1= 
|
| 1 | 1 | 1 | 0 | 1  b b  c= c= 
|
| 1 | 1 | 1 | 1 | 
|
Проверим, не равна ли наша функция функциям:
 ,
,  ,
,  ,
, 
и их инверсиям:
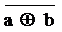 ,
,  ,
,  ,
,  .
.
Для этого получим соответствующие векторы этих линейных ПФ (табл. 30).
Таблица 30
Векторы переключательных функций
| Переменные |
|
|
|
|
|
|
|
| ||
| a | b | c | ||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
Видим, что ни один из полученных векторов этих восьми линейных ПФ не совпадает с вектором нашей функции.
Следовательно, функция №17410 – не линейная.
4. Определим, обладает ли наша ПФ свойствами самодвойственности.
Для этого проанализируем её вектор в двоичном коде (рис. 38).

Рис. 38. Вектор в двоичном коде
Видим, что симметричные разряды 5 и 2 неортогональны. Следовательно, ПФ – несамодвойственна. У самодвойственной ПФ симметричные разряды ортогональны (противоположны).
5. Определим, монотонна ли наша ПФ.
Посмотрим на куб соседних чисел. Монотонная функция по всем возможным путям из вершины (000) в вершину (111) монотонна. Однако наша функция на наборе (010) принимает значение «1», а на большем сравнимом наборе (110) – «0». Следовательно, она не монотонна.
Представим вектор свойств ПФ (табл. 31):
Таблица 31
Вектор свойств ПФ
| 1 | 2 | 3 | 4 | 5 | № свойства |
| 1 | 1 | 0 | 0 | 0 | наличие свойства |
В восьмеричном коде вектор свойств равен 308, а в шестнадцатеричном – 1816.
ОСНОВНЫЕ ЗАКОНЫ БУЛЕВОЙ АЛГЕБРЫ
И ПРЕОБРАЗОВАНИЕ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ










