Анимация корневого объекта

Корневой объект Model включает три экземпляра объекта counter и один экземпляр объекта Gen. Когда мы откроем окно анимации корневого объек­та, мы увидим уже помещенные туда три одинаковых изображения разрядов счетчика и одно изображение генератора. Их расположение в поле анима­ции соответствует расположению соответствующих экземпляров активных объектов в окне структуры объекта Model.

Запустите модель на выполнение. Вы увидите, что значения на изображени­ях разрядов счетчика будут отражать состояния этих разрядов.

Достройте анимацию в соответствии с тем, как она представлена в модели

ContinuousCounter3.

5.3. Заключение: поддержка моделирования непрерывных процессов в AnyLogic

В этой главе были изучены некоторые концепции AnyLogic и средства, под­держивающие моделирование непрерывных процессов. Рассмотрим повтор­но эти концепции по порядку.

Активные объекты

Определение класса активного объекта задает шаблон, и отдельные его эк­земпляры могут использоваться как составные блоки других активных объ­ектов. Вся модель представляется как набор классов активных объектов, ка­ждый из классов может включать произвольное число объектов-экземпляров других классов. Активный объект определяется своей структурой (составом включенных в него объектов) и поведением, которое изменяет со временем состояние активного объекта. Корнем иерархии включений экземпляров

классов активных объектов является класс активного объекта, по умолчанию получающий имя Main, представляющий собственно разрабатываемую мо­дель со своим единственным экземпляром с предопределенным именем root.

Переменные

Непрерывные процессы задаются в AnyLogic очевидным образом: определе­нием вещественных переменных формулами и уравнениями (алгебраиче-скими и дифференциальными) в их привычной аналитической записи. Пе­ременные в модели определяют состояние динамического объекта, они изменяются с течением времени по законам, определяемым уравнениями и формулами. Значения переменных можно изменять и контролировать. У каждого экземпляра активного объекта существует свой набор перемен­ных и свой набор параметров, поэтому поведения различных экземпляров одного и того же активного объекта могут быть различны.

Переменные могут быть либо внутренними (переменные состояния объекта), либо интерфейсными. Связи по интерфейсным переменным в AnyLogic яв­ляются направленными: переменные могут быть определены в одном актив-ном объекте, а их значения использоваться в других.

Переменные также могут быть скалярного либо векторного типа. Изменение скалярных переменных в процессе выполнения модели могут отображаться вграфиках. Векторный тип в AnyLogic определяется как "матрица", и он наиболее удобен при работе с прямоугольными матрицами. AnyLogic пре­доставляет средства для операций над матрицами. Кроме таких простых операций, как сложение и умножение, с переменными этого типа также возможны и многочисленные специальные операции линейной алгебры: обращение, транспонирование, LU-декомпозиция, выделение и операции на подматрицах и т. п. Переменные типа Массив используются для пред­ставления многомерных массивов вещественных значений.

5.3.3. Формулы, системы алгебраических
и дифференциальных уравнений

Непрерывное изменение во времени значений переменных в AnyLogic мож-но описывать с помощью формул, дифференциальных и алгебраических уравнений. Уравнения можно задавать как для скалярных переменных, так и для матриц. Уравнения и формулы могут быть связаны с активным объек-том и с любым состоянием стейтчарта. Дифференциальные уравнения зада­ются в форме Коши, т. е. в виде d (x)/ dt = F (x, у, t,). Здесь F (x, у, t,...) — ари фметическое выражение, в которое может входить специальный символ t обозначающий модельное время.

Алгебраические уравнения задаются в форме 0 = F(x, у, t,), где х — пере-менная типа double или матричного типа. Для каждой системы алгебраиче-

ских уравнений должны быть явно определены неизвестные переменные с помощью следующего оператора: find(x, у,...). Имя переменной или вызов функции можно вставить в уравнение с помощью мастера автомати­ческого ввода, который представляет собой список, содержащий перемен­ные (значок ), параметры (значок 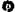) и функции (значок ), отсортированные по алфавиту. Вы можете просто выбрать имя из списка, и оно будет автоматически вставлено в выражение. Для вызова мастера необходимо щелкнуть по кнопке , после чего двойной щелчок мыши на

выбранном имени позволит вставить соответствующий элемент из списка мастера в поле, в котором записывается выражение. Мы используем эту возможность в главе 13.

Алгебраические и дифференциальные уравнения в AnyLogic решаются чис­ленно. AnyLogic использует современную библиотеку численных методов решения систем обыкновенных дифференциальных уравнений (как линей­ных, так и нелинейных), алгебраических уравнений (связывающих вещест­венные переменные) и любых их комбинаций, решения как жестких, так и нежестких систем. При проведении компьютерных экспериментов (изменяя настройки окна свойств Эксперимента) пользователь может самостоятельно выбрать численный метод из данной библиотеки либо доверить это испол­нительной системе, которая автоматически выберет наилучший из них. Ис­пользуя установки эксперимента, пользователь может задать требуемые ему точность решения систем (временную, относительную и абсолютную) и шаг по времени. Разработчик модели может также подключить и использовать свои численные методы.

Параметры

В отличие от переменных, параметр — это характеристика объекта, то, что может изменяться вне объекта. Как правило, сам объект свои параметры не изменяет. Параметры модели часто называют "факторами", они являются для объекта статическими величинами, которые различаются у разных эк­земпляров одного и того же класса, тем самым позволяя иметь в модели различные представления одного и того же шаблона. Параметры одного объекта могут быть изменены в различных прогонах модели, или же пользо­ватель может их изменять интерактивно при выполнении модели в текущем эксперименте с помощью слайдеров, окон редактирования или непосредст­венно в дереве корневого объекта root.

Параметр может быть простым и динамическим. Простой параметр — это константа. Предполагается, что значение простого параметра не изменяется при выполнении модели, но различные прогоны модели могут выполняться при различных значениях простого параметра. Динамический параметр имеет совершенно другую природу. Обращение к нему при выполнении модели вызывает выполнение некоторого кода (функции). Иными словами, каждый

раз при использовании такого параметра (при доступе к нему) его значение перевычисляется. В качестве значения динамического параметра может сте­ять вызов функции или любое выражение, возвращающие значение соответ-ствующего типа. При определении класса активного объекта значения его параметров могут не задаваться, их тогда следует определить для экземпля­ров этого класса.