В результате многочисленных экспериментов на моделях и в натуре и общих теоретических соображениях соображений установлено сопротивление жидкости движению в ней твердого тела зависит в основном от плотности и вязкости жидкости, размеров, характера поверхности и формы тела, скорости его движения относительно жидкости.
В соответствии с этим общее выражение для силы сопротивления Rх представляется формулой:
Rх=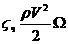 
,
где: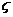 
- безразмерный коэффициент, носящий название коэффициента сопротивления тела, определяется опытным путем, 
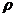- плотность жидкости, V – относительная скорость движения тела и жидкости, Ω – площадь, которая в основном характеризует сопротивление тела (если основными являются силы трения, то за Ω принимают смоченную поверхность судна; если силы трения имеют второстепенное значение, то за Ω принимают наибольшую площадь сечения тела плоскостью, перпендикулярной к направлению движения).
За Ω часто принимают среднюю площадь поперечного сечения судна, определяемую как частное от деления объемного водоизмещения W на длину судна L.
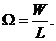
Следует отметить, что величина коэффициента сопротивления тела 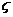x тесно связана с выбором характерной площади Ω и относится только к выбранной площади. Другими словами, если для одного и того же тела мы будем принимать различные Ω, то для каждой Ω нужно будет определять свой коэффициент 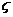x.
Выражение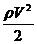 
можно рассматривать как запас кинетической энергии в единице объема жидкости.
Несмотря на то, что каждое из сопротивлений R тр, R вихр, Rволн имеют отличную от других сопротивлений физическую природу и законы изменения можно записать:
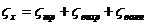
где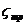 
- коэффициент сопротивления трения; 
- коэффициент вихревого сопротивления;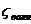 
- коэффициент волнового сопротивления. 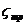вычисляют по элепирическим формулам, а и 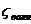объединяют и называют остаточным сопротивлением.
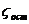
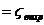
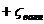
6.3. ПОДЪЁМНАЯ СИЛА
6.3.1. Теорема Жуковского о подъёмной силе
Подъёмная сила - составляющая полной силы давления жидкой или газообразной среды на движущееся в ней тело, направленная перпендикулярно к скорости тела (к скорости центра тяжести тела, если оно движется непоступательно).
Согласно теореме Жуковского ( сформулирована Н. Е. Жуковским в 1904. ) подъёмная сила, действующая на тело в потоке жидкости или газа, обусловлена связанными с обтекаемым телом вихрями (присоединёнными вихрями), причиной возникновения которых является вязкость жидкости. Наличие этих вихрей приводит к обтеканию крыла потоком с отличной от нуля циркуляцией скорости. Если установившийся плоскопараллельный потенциальный поток (потенциальный поток - безвихревое течение жидкости, при котором каждый малый объём деформируется и перемещается поступательно, не имея вращения) несжимаемой жидкости набегает на бесконечно длинный цилиндр перпендикулярно его образующим, то на участок цилиндра, имеющий длину вдоль образующей, равную единице, действует подъёмная сила Y, равная произведению плотности среды на скорость v потока на бесконечности и на циркуляцию Г скорости по любому замкнутому контуру, охватывающему обтекаемый цилиндр, т. е.
Y =ρ vГ.
Направление подъёмной силы получается из направления вектора скорости на бесконечности поворотом его на прямой угол против направления циркуляции. Теорема Жуковскогосправедлива и при дозвуковом обтекании профиля сжимаемой жидкостью (газом). Для звуковой и сверхзвуковых скоростей обтекания теорема Жуковского в общем виде не может быть доказана.
Теорема Жуковского легла в основу современной теории крыла и гребного винта. С помощью теоремы Жуковского могут быть вычислены подъёмная сила крыла конечного размаха, тяга гребного винта, сила давления на лопатку турбины и компрессора и др.
Таким образом, подъёмная сила возникает вследствие несимметрии обтекания тела средой. Например, при обтекании крыла самолёта (рис. 1) частицы среды, обтекающие нижнюю поверхность, проходят за тот же промежуток времени меньший путь, чем частицы, обтекающие верхнюю, более выпуклую поверхность и, следовательно, имеют меньшую скорость.
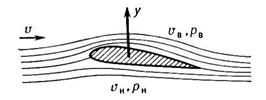
Рис. 1. Обтекание профиля крыла самолёта
Скорость Vн < Vв, давление рн>рв, Y - подъёмная сила крыла.
Но, согласно Бернулли уравнению, там, где скорость частиц меньше, давление среды больше и наоборот. В результате давление среды на нижнюю поверхность крыла будет больше, чем на верхнюю, что и приводит к появлению подъёмной силы.
Несимметричное обтекание крыла можно представить как результат наложения на симметричное течение циркуляционного потока вокруг контура крыла, направленного на более выпуклой части поверхности в сторону течения, что приводит к увеличению скорости, а на менее выпуклой - против течения, что приводит к её уменьшению. Тогда подъёмная сила Y будет зависеть от величины циркуляции скорости Г и, согласно Жуковского теореме, для участка крыла длиной L, обтекаемого плоскопараллельным потоком идеальной несжимаемой жидкости,
Y = ρu ГL,
где ρ - плотность среды, u - скорость набегающего потока.
Поскольку Г имеет размерность [ulρ], то подъемную силу можно выразить равенством обычно применяемым в аэродинамике:
,
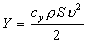где S - величина характерной для тела площади (например, площадь крыла в плане), су - безразмерный коэффициент подъемной силы зависящий от формы тела, его ориентации в среде и чисел Рейнольдса Re и Маха М. Значение су определяют теоретическим расчётом или экспериментально.
