Изменяемость объема жидкостей и газов под действием температуры и давления

КОНСПЕКТ ЛЕКЦИЙ ПО УЧЕБНОЙ ДИСЦИПЛИНЕ

 «ГИДРОГАЗОДИНАМИКА»

Направление/специальность: __ 20.03.01 Техносферная безопасность _

                                                                                    (код, наименование специальности /направления)

Профиль/специализация: Безопасность жизнедеятельности в техносфере

Квалификация (степень) выпускника: __ бакалавр _____ ____________ __ Форма обучения: __                                       заочная_________ ___ ____

МОСКВА

Раздел 1. ОСНОВЫ ГИДРОСТАТИКИ.

 

Содержание:

1.1. Основные физические свойства жидкостей и газов.

1.2. Гидростатика.

 

 

ОСНОВНЫЕ ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ И ГАЗОВ

Характеристика жидкостей и газов

Жидкостью называется физическое тело, обладающее легкой подвижностью частиц, то есть текучестью.

Жидкости с точки зрения физико-механических свойств разделяются на два класса - капельные жидкости (или малосжимаемые) и газы (или сжимаемые жидкости). Жидкость рассматривается в гидравлике обычно как сплошная (непрерывная), однородная и изотропная среда, обладающая одинаковыми свойствами во всех точках и по всем направлениям.

Основными физическими свойствами жидкости и газов, базируясь на которых в гидравлике устанавливаются общие законы ее равновесия и движения, являются:

1) текучесть, 2) весомость, 3) изменяемость объема и 4) вязкость.

Текучесть

Текучестью называется неспособность жидкости сопротивляться внутренним сдвигающим усилиям, вызванным сколь угодно малыми силами.

Свойство текучести выражает физически главное отличие жидкого тела от твердого тела.

Вследствие текучести, жидкость, находясь в покое, растекается под действием собственного веса и принимает форму того сосуда, в котором находится. Растекаясь в сосуде и занимая часть его объема, жидкость всегда образуют свободную поверхность.

Газы, растекаясь, всегда занимают весь объем сосуда и не образуют свободной поверхности.

Удельный вес и плотность

Удельным весом g называется вес единицы объема жидкости, который определяется по формуле

,                                                 (1.1)

где: G – вес жидкости в объеме W.

Удельный вес - величина размерная. Его размерность

Плотностью r называется масса, заключенная в единице объема жидкости, которая определяется по формуле

                                                   (1.2)

где: М - масса жидкости, заключенная в объеме W.

Размерность плотности:

в системе СИ

Зависимость между удельным весом и плотностью жидкости легко получить, помня, что по второму закону Ньютона

G = Mg.

 Разделив обе части уравнения на объем W, получим

g = r g.                                                       (1.3)

Это равенство выражает второй закон Ньютона, записанный для единицы объема жидкости.

Удельный объем V – объем единицы массы вещества - величина, обратная плотности.

V = W/m=1/ρ.

Размерность – [м3/кг].

 

Изменяемость объема жидкостей и газов под действием температуры и давления

Изменяемость объемаот давления и температуры для капельных жидкостей.

Свойство жидкости изменять объем под действием давления называется сжимаемостью и характеризует упругость жидкости.

Изменение объема жидкости  при изменении давления на 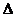р (рис. 1.1)

                                       (1.4)

Величина , характеризующая изменение объема жидкости при изменении давления, отрицательна, так как при сжатии жидкости положительному приращению давления соответствует отрицательное приращение объема.

Сжимаемость жидкости оценивается коэффициентом объемного сжатия b_w

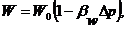
 соответственно        (1.5)

где: W ₀   - начальный объем жидкости; ΔW - изменение объема при изменении давления на Δ p.

Коэффициент объемного сжатия b _w представляет собой относительное уменьшение объема жидкости (по отношению к начальному объему) при увеличении давления на единицу и имеет размерность обратную размерности давления

 

                                                   Рис. 1.1

Величина обратная коэффициенту объемного сжатия является модулем упругости жидкости при всестороннем сжатии

                                        (1.6)

Капельные жидкости, как и твердые тела, представляют собой малосжимаемую, малоупругую среду (модуль упругости воды E=2,1.10³ кгс/см², стали E=2.10⁶ кгс/см²). В связи с этим при решении очень многих практических задач гидравлики сжимаемостью жидкости можно пренебречь, полагая, что жидкость не изменяет своего объема при изменении давления (b_w=0), а, следовательно, ее удельный вес и плотность остаются постоянными: g=const и r=сonst.

В отдельных случаях сжимаемость должна учитываться, например, при гидравлическом ударе, связанном с упругими колебаниями жидкости.

Температурное расширение - изменение объема жидкости при увеличении температуры при Р = const.

Изменение объема жидкости  при изменении температуры на 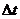 равно

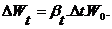                                        (1.7)

Изменение объема жидкости при изменении температуры характеризуется коэффициентом объемного (температурного) расширения b _t.

 соответственно       (1.8)

где: W - начальный объем жидкости;

     dW - изменение объема при изменении температуры на Δt.

Величина b _t выражает относительное изменение объема жидкости при изменении температуры на единицу и имеет размерность

Объем жидкости с увеличением температуры увеличивается. Однако это увеличение незначительно. Например, у воды при изменении температуры от 0 до 100°С при давлениях от I до 100 ат величина b _t изменяется в пределах

,

т.е.достигает максимум 0,07 % при увеличении температуры на 1°С, Поэтому при решении многих практических задач влиянием изменения объема жидкости при изменении температуры на величину ее удельного веса и плотности можно пренебречь, полагая b_t = 0, а, следовательно, g = const и r = const. Однако, следует учитывать, что увеличение объема жидкости при повышении температуры может вызвать опасные последствия, например, разрушение гидравлической системы, в которой заперты без возможности расширения значительные объемы жидкости и т.п.

Изменяемость объемаот давления и температуры для газов.

В отличие от капельных жидкостей газы характери­зуются значительной сжимаемостью и высокими значе­ниями коэффициента температурного расширения.

Характерной особенностью изучения сжимаемых жидкостей является необходимость учитывать соотношение между давлением p, плотностью (удельным весом) g= g r, удельным объемом  и температурой T °К (Кельвина).

Это соотношение, устанавливающее зависимость между физическими величинами, определяющими состояние газа (давлением газа р, его объёмом V и абсолютной температурой Т) называется уравнением состояния.

Для идеального газа уравнение состояния (уравнение Клапейрона - Менделеева) записывается в следующем виде:

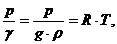или  (1.9)

 где: R = 29,27 м/°К – универсальная газовая постоянная;

     g = 9,81 м/c² - ускорение силы тяжести.

Газовая постоянная имеет физический смысл работы расширения 1 моля (моль - число граммов химического вещества, равное его молекулярной массе) идеального газа под постоянным давлением при нагревании на 1°. Газовая постоянная обычно численно выражается в следующих единицах: 8,3143 ± 0,0012 дж/град-моль, 8,314-10⁷ эрг/град-моль, 1,986 кал/град-моль, 82,05-10^-3 л·атм/град-моль.

Универсальная газовая постоянная, отнесённая не к 1 молю, а к 1 молекуле, называется постоянной Больцмана. Постоянная Больцмана - одна из основных физических постоянных, равная отношению универсальной газовой постоянной R к числу Авогадро N_A

k = R/N_A (k = (1,38054±0,00018)´10^-23дж/К).

(Число Авогадро - число молекул в 1 моле любого вещества, оно одинаково и равно 6,02252^.10²³. Моль любых веществ, находящихся в состоянии идеального газа, при нормальных условиях [0°С и давлении 101325 н/м ² (760 мм. рт. ст.) ] занимают приблизительно один и тот же объём, равный 22,4 л).

Для газа, имеющего общую массу М и молекулярную массу μ, уравнение состояния записывается в виде

 или pV=NkT, (1.10)

где N - число частиц газа, k - Больцмана постоянная.

Уравнение состояния представляет собой уравнение состояния идеального газа, которое объединяет Бойля - Мариотта закон (зависимость между р и V при Т = const), Гей-Люссака закон (зависимость V от Т при р = const) и Авогадро закон (согласно этому закону, газы при одинаковых значениях р, V и Т содержат одинаковое число молекул N).

Уравнение Клапейрона - наиболее простое уравнение состояния, применимое с определённой степенью точности к реальным газам при низких давлениях и высоких температурах (например, атмосферный воздух, продукты сгорания в газовых двигателях и др.), когда они близки по своим свойствам к идеальному газу.

Наиболее простыми свойствами обладает газ, разре­женный настолько, что взаимодействие между его мо­лекулами может не учитываться, так называемый совер­шенный (идеальный) газ. Для совершенных газов спра­ведливо уравнение Клапейрона, позволяющее определять плотность газа при известных давлении и температуре, т. е.

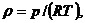             (1.11)

где р - абсолютное давление; R - удельная газовая постоянная, различная для разных газов, но не зависящая от температуры и дав­ления [для воздуха R =287 Дж/(кг ^. К)]; Т - абсолютная темпера­тура.

Поведение реальных газов в условиях, далеких от сжижения, незначительно отличается от поведения со­вершенных газов, и для них в широких пределах можно пользоваться уравнениями состояния совершенных га­зов.

В технических расчетах плотность газа обычно при­водят к нормальным физическим условиям (t=0°С; Р=101325 Па) или к стандартным условиям (t=20°С; р=101325 Па).

Плотность воздуха при R=287 Дж/(кг ^. К) в стан­дартных условиях по формуле (1.11) будет

При других условиях плотность воздуха определяется по формуле

(1.12)

Для изотермического процесса (T=const) из форму­лы (2.10) имеем

p/ρ= const,                            (1.13)

а для адиабатического процесса

р/ρ ^k = const,                          (1.14)

где k = c_p/ c_v - адиабатическая постоянная газа (здесь с _p - тепло­емкость газа при постоянном давлении; с_v - то же, при постоянном объеме).

Сжимаемость газов зависит от характера процесса изменения состояния:

для изотермического процесса

E₀= p.                                     (1.15)

а для адиабатического

Е₀ = kp.                                (1.16)

 

Из выражения (19) следует, что изотермическая сжимаемость для атмосферного воздуха составляет ~9,8-10⁴Па, что примерно в 20 тыс. раз превышает сжимаемость воды.

Сжимаемость сплошной среды можно также характеризовать отношением приращения давления dp  к приращению ее плотности d r. Характеристикой, определяющей зависимость изменения плотности газа при изменении давления в движущемся потоке, явля­ется скорость распространения звука а.

В однородной среде ско­рость распространения звуковых колебаний, как отмечено выше, определяется из выра­жения.

а²= dp/ dρ.                             (1.17)

С учетом соотношений (8) и (9) из выражения (21) находим скорость звука в виде зависимости

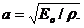  (1.18)

Для адиабатического процесса из выражений (18) и (14) сле­дует: dp/ dρ =kр/ρ=kRT, откуда для газов

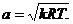                           (1.19)

Скорость распространения звука (при t=20°С) в воздухе со­ставляет 330 м/с, в углекислом газе - 261 м/с, в воде - 1480 м/с.

Поскольку объем газа в большой мере зависит от температуры и давления, выводы, полученные при изуче­нии капельных жидкостей, можно распространять на га­зы лишь в том случае, если в пределах рассматриваемо­го явления изменение давления и температуры невелико.

Значительные разности давлений, вызывающие сущест­венное изменение плотности газов, могут возникнуть при движении газов с большими скоростями. Соотноше­ние между скоростью движения жидкости и скоростью звука в ней позволяет судить о необходимости учета сжимаемости в каждом конкретном случае. Практически газ можно принимать несжимаемым при скоростях движения, не превышающих 100 м/с.