Прочностные и деформационные свойства стенок кровеносных сосудов и изменение этих свойств (с возрастом) имеет большое значение для медицины.
Кровеносные сосуды состоят из трех концентрических слоёв: внутренний – интима; средний – средняя сосудистая оболочка; наружный – внешняя сосудистая оболочка.
Механические свойства кровеносных сосудов обуславливаются, главным образом, свойствами средней сосудистой оболочки, состоящей из коллагена, эластина и гладких мышечных волокон.
Представим таблицу допускаемых деформаций этих элементов.
| Элемент | Деформация ε (%) | Модуль Юнга (МПа) |
| Эластин | 200-300 | 0,1 – 0,6 |
| Коллаген | до 10 | 10 – 100 |
| Мышечное волокно (при сокращении) | 20 | 0,01 – 0,1 |
| Кровеносный сосуд | 5-50 | 0,06 – 0,7 |
Следует отметить, что гладкие мышечные клетки могут менять свою длину (сокращаться) под действием нервных или химических стимуляторов. Гладкая мышца осуществляет активное поведение кровеносных сосудов, так как в результате её сокращения меняется диаметр кровеносного сосуда и механические свойства сосудистой стенки в целом. Таким образом, достигается оптимальное распределение и регулирование кровяного потока.
Содержание трёх основных компонентов сосудистой ткани меняется для различных мест стенки. Отношение эластина к коллагену в сосудах ближе к сердцу равно 2:1, но оно убывает с удалением от него и в бедренной артерии оно равно 1:2. С удалением от сердца увеличивается содержание гладких мышечных волокон, и уже в артериолах они становятся основной составляющей сосудистой ткани.
Установлено, что сосудистая ткань является практически несжимаемой. Кровеносные сосуды обладают криволинейной ортотропией, т.е. их механические свойства в радиальном, осевом и кольцевом направлениях существенно различны.
Механическое поведение сосудов усложняется ещё и тем, что в организме они находятся под влиянием окружающих тканей, растянуты в продольном направлении и их деформации в этом направлении ограничены. В сосудах наблюдаются значительные отклонения механических характеристик для отдельных индивидов от установленных средних значений.
Напряжение, возникающее при деформации в стенке кровеносного сосуда, определяется уравнением Ламе.
Вывод уравнения Ламе
Возьмём часть кровеносного сосуда длиной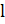 
и толщиной стенки 
. Представим стенки сосуда вдоль и поперёк:
Две половины цилиндрического сосуда взаимодействуют между собой по сечениям стенок сосуда. Общая площадь сечения взаимодействия будет 
, тогда сила взаимодействия двух половинок:
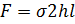
Эта сила уравновешивается силами давления крови изнутри:
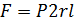
Таким образом, имеем:
,
Откуда:
уравнение Ламе
Таким образом, напряжение, возникающее в стенках кровеносных сосудов, зависит от величины давления крови, внутреннего радиуса и от толщины стенок кровеносного сосуда.
