Методами термодинамики можно показать, что зависимость энергии Гиббса k -го компонента идеального газа от его парциального давления (Рk) выражается соотношением (речь идет об абсолютном значении энергии Гиббса!):
. (2.1)
Для реального газа это соотношение принимает вид:
. (2.2)
Аналогично выражения для энергии Гиббса m -го компонента идеального и реального растворов имеют вид (речь идет об абсолютном значении энергии Гиббса!):
,
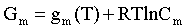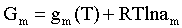. (2.3)
Обратим внимание, что значения функций gk(T) и gm(T) неизвестны и поэтому неизвестны абсолютные величины энергий Гиббса. Кроме того, в силу логарифмической зависимости энергии Гиббса от давления (концентрации) нельзя принимать за стандартное состояние газообразных веществ и растворов (в отношении растворенных веществ) бесконечно разреженный газ и бесконечно разбавленный раствор соответственно.
Изменение энергии Гиббса в химической реакции может быть найдено и через абсолютные величины энергий Гиббса компонентов, если бы они были известны:
(продуктов) – 
(исходных веществ), (2.4)
где ni и nj – числа молей (коэффициенты в уравнении). Рассмотрим равновесную газовую систему, подставим выражение (2.1) в соотношение (2.4):
Первые слагаемые этой суммы являются функцией только температуры и в дальнейшем обозначим их через Ф(Т). С остальными слагаемыми выполним несложные математические преобразования, в результате получаем:
= Ф(Т) + 
- 
=
. (2.5)
При равновесии DGреакции = 0, с учетом этого для выражения (2.5) получаем:
. (2.6)
Логарифм отношения произведений является функцией только температуры:
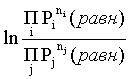
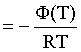, (2.7)
и пусть он равен lnKP. Выражение
, (2.8)
являющееся константой при данной температуре, называется константой равновесия. Для равновесной смеси реальных газов константа равновесия будет иметь такой же вид, но вместо давлений в ней будут фигурировать фугитивности. Повторяя эти выкладки с выражением для энергии Гиббса компонента раствора (2.3), получаем аналогичное выражение:
. (2.9)
В случае реальных растворов концентрации должны быть заменены на активности.
Для газовых равновесий величины Кр и Кс связаны:
(2.10)
Например, для равновесной системы
.
Уравнение (2.5) является общим выражением для энергии Гиббса химической реакции. Подставляя в него соотношения (2.7 – 2.9) получаем:
(газы);
(2.11)
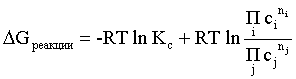(растворы).
При Pi, Pj, ci и cj, равных единице (стандартное состояние!) эти соотношения переходят в одно из наиболее употребляемых уравнений термодинамики:
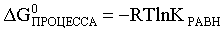. (2.12)
Подчеркнем, что в уравнении (2.11) фигурирует термодинамическая константа, она равна Кр или Кс лишь в случае идеального газа или идеального раствора соответственно. Для реальных систем в выражении термодинамической константы равновесия должны быть подставлены величины фугитивностей компонентов газовой смеси или активностей компонентов раствора.
Под знаком логарифма в (2.11) стоят отношения двух величин, выраженных в одних и тех же единицах, – отношение давления к давлению в стандартном состоянии или отношение концентрации к концентрации в стандартном состоянии, то есть безразмерные величины. Таким образом, термодинамическая константа равновесия, стоящая под знаком логарифма в выражении (2.11), является безразмерной величиной. Наконец, отметим, что концентрация индивидуальных жидких и кристаллических веществ постоянна и равна единице и не включается в выражение константы равновесия.
Уравнение (2.12) является одной из основ экспериментального определения стандартных величин энергий Гиббса процессов, в частности – энергий Гиббса образования соединений. Среди других поставщиков термодинамических данных отметим электрохимические измерения. Наконец, подчеркнем, что основным поставщиком термодинамических данных являются калориметрические измерения, позволяющие определять энтальпии и внутренние энергии различных процессов, теплоемкости веществ и систем, что дает возможность определять энтальпии образования соединений и энтропии индивидуальных веществ.
Вернемся теперь к концентрационной и температурной зависимости электродного потенциала. Объединим уравнения (1.20), (1.28) и (2.10) для реального раствора:
. (2.13)
Отсюда ЭДС электрохимической системы равна:
(2.14)
При активностях компонентов, равных единице (стандартное состояние!), это уравнение переходит в
. (2.15)
Сочетая (2.14) и (2.15), получаем
. (2.16)
С учетом сказанного в разделе 1.6, соответствующее выражение для электродного потенциала имеет вид:
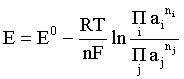. (2.17)
Например, для электродных процессов:
Ni2+ + 2 ē = Ni; E1
Fe3+ + ē = Fe2+; E2
MnO4– + 8H+ + 5 ē = Mn2+ + 4 H2O; E3
выражения для электродных потенциалов будут следующими:
;
;
.
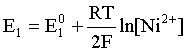
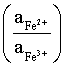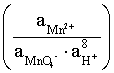Обратим внимание, что, меняя концентрации потенциалопределяющих ионов, можно значительно изменять величину, а порой и знак электродного потенциала. Конкретные примеры, иллюстрирующие это, приведены в разделе "Задачи и упражнения" (с. 28).
Задачи и упражнения
