Значимость стандартных шкал заключается прежде всего в том, что они позволяют отражать в одинаковых единицах измерения разнородные параметры, которые в обычных для этих параметров единицах измерения несопоставимы.
Соотношения двух или нескольких показателей, имеющих совместное распределение, могут характеризоваться:
строгим соответствием каждого значения одного показателя определенному значению другого показателя — функциональная взаимосвязь;
соответствием каждого значения одного показателя нескольким более или менее близким значениям другого показателя — статистическая взаимосвязь;
отсутствием связи между значениями показателей.
Графическое представление результатов измерения двух показателей, между которыми оценивается взаимосвязь, называется диаграммой рассеяния, или корреляционным (от лат. corre- latio — соотношение, соответствие) полем. В прямоугольной системе координат по одной из осей откладывают значения 1-го показателя, по другой — соответствующие им значения 2-го показателя. Совокупность полученных точек имеет более или менее компактный вид (в зависимости от вариации результатов измерения), большую или меньшую вытянутость вдоль некоторой средней линии (в зависимости от теСноты связи), больший или меньший наклон этой линии (в зависимости от регрессии показателя). Помимо линейных форм зависимости, встречаются и нелинейные взаимосвязи, которые здесь не рассматриваются.
Теснота и направленность взаимосвязи показателей оцениваются с помощью коэффициента корреляции (г). Значение коэффициента корреляции находится в пределах от -1 до +1. Интерпретация значений коэффициента корреляции зависит от объема выборки (числа степеней свободы) и выбранного уровня значимости (табл. 8.4).
Таблица 8.4
Границы для выборочного коэффициента корреляции (уровень значимости 0,1; 0,05; 0,01)
| Число степеней свободы | Коэффициент корреляции | ||
| 0,1 | 0,05 | 0,01 | |
| 2 | 0,900 | 0,950 | 0,990 |
| 3 | 0,805 | 0,878 | 0,959 |
| 4 | 0,729 | 0,811 | 0,917 |
| 5 | 0,669 | 0,754 | 0,874 |
| 6 | 0,622 | 0,707 | 0,834 |
| 7 | 0,582 | 0,666 | 0,798 |
| 8 | 0,549 | 0,632 | 0,765 |
| 9 | 0А21 | 0,602 | 0,735 |
| 10 | 0,497 | 0,576 | 0,708 |
| 20 | 0,360 | 0,423 | 0,537 |
| 30 | 0,269 | 0,349 | 0,449 |
| 50 | 0,231 | 0,273 | 0,354 |
Знак коэффициента корреляции имеет следующий смысл: «плюс» — прямая пропорциональная (положительная) взаимосвязь; «минус» — обратная (отрицательная) взаимосвязь.
Если измерения произведены в шкале отношений или интервалов и форма взаимосвязи —: линейная, рассчитывают парный линейный коэффициент корреляции Пирсона (гА):
(8.17)
где хну — средние арифметические значения показателей х и у; <5хъсУ — средние квадратические отклонения этих показателей; п — число сравниваемых результатов измерения (число пар).
Доля вариации одного показателя, которую можно объяснить за счет вариации другого показателя, называется коэффициентом детерминации (£>). Он рассчитывается по формуле (8.18)
Наклон графика линейной зависимости (линия проводится как продолжающаяся длинная ось «эллипса» рассеяния) зависит от того, насколько изменяется значение одного показателя при изменении значений другого на единицу. Эта величина называется коэффициентом регрессии (Ь), а график регрессии (рис. 8.3) описывается уравнениями (8.19)-(8.23).
Рис. 8.3. Корреляционное поле (а) и линии регрессии (б). Пример положительной зависимости
у = а + Ьх, (8.19)
где х — значение 1-го показателя; у — соответствующие ему значения 2-го показателя; а — смещение по оси у (свободный член уравнения).
на основе которых рассчитываются относительные погрешности в %:
Взаимосвязь показателей, измеренных в ординальной шкале, оценивается с помощью ранговых коэффициентов корреляции. Ранговый коэффициент Спирмэна (р) вычисляется по формуле (8.24)
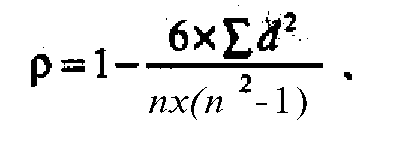
где d = dx- dy — разность рангов данной пары измерений оцениваемых показателей; п — объем выборки (число пар измерений).
Значения коэффициента корреляции Спирмэна, так же как и коэффициента корреляции Пирсона, находятся в пределах от - 1 до + 1.
Взаимосвязь показателей, измеряемых в шкале наименований, оценивается с помощью коэффициентов сопряженности. Если показатели варьируют альтернативно (например: «да» — А;«нет» — В; «муж.» — С; «жен.» — JD), то используют тетрахорический коэффициент сопряженности (8.25)
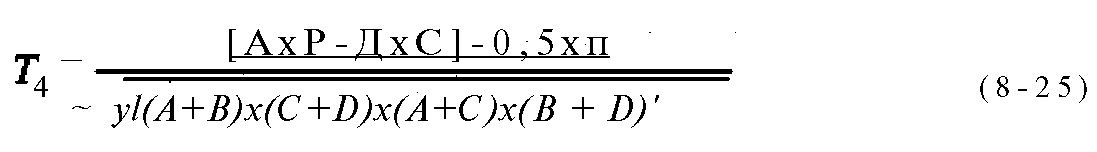
Коэффициент Т4 изменяется в пределах от -1 до +1.
При анализе взаимосвязи показателей, имеющих большее (илитакое же) количество классов варьирования, используется критерий согласия Пирсона (х). Критерий х рассчитывается по формуле (8.26)
(8.26)
где О — значение частоты в данной ячейке таблицы сопряженности; Е — ожидаемое значение частоты в данной ячейке таблицы сопряженности (табл. 8.5).
Таблица 8.5
Пример вычисления коэффициента %
| Номера | Взвешенные возведенные | |||||
| Номера строк | столбцов | Суммы | Ожидаемые частоты (£) | в квадрат отклонения | ||
| 1 | 2 | 3 | по строкам Щ | действительных частот от ожидаемых (0-Е) Е | ||
| 1 | 8 | 8 | 1 | 17 | 5,37 6,71 4,92 | 1,29 0,25 3,12 |
| 2 | 4 | 7 | 10 | 21 | 6,63 8,29 6,07 | 1,04 0,20 2,54 |
| ЕД, | 12 | 15 | 11 | 38 | - | Х2=8,44 |
Ожидаемые частоты рассчитываются по формуле (8.27)
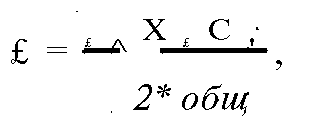где IM1 — сумма частот в данном столбце таблицы сопряженности; ЕС, — сумма частот в данной строке таблицы сопряженности; Л'овщ — общая сумма частот по всем столбцам (или по всем строкам).
Значение критерия Пирсона сравнивается с табличными критериями значениями х для степени свободы v и уровней значимости 0,05 и/или 0,01. Количество степеней свободы v рассчитывается по формуле (8.28)
У = (Л-1)х(С-1), (8.28)
где R — число столбцов; С — число строк.
Если полученное значение х2 превышает критическое значение x2 ov, приведенное в табл. 8-6, значит, между сравниваемыми показателями имеется статистическая связь, отличающаяся от нуля с вероятностью 0,95 или 0,99.
Уровень значимости (а) характеризует вероятность отклонения, признаваемого невозможным в силу лишь случайных. причин. Применительно к х2, если рассчитанная величина достигаетуровня значимости 0,05, это свидетельствует, что при отсутствиисвязи между сравниваемыми показателями такое значение х встречается не чаще, чем 5 раз на 100 наблюдений.
Таблица 8.6.
Критические значения %2 -критерия, соответствующие разным уровням значимости (а) и числам степени свободы (v)
| Степень свободы V | Уровень значимости а | ||||
| 0.1 | 0,05 | 0,02 | 0,01 | 0,001 | |
| 1 | 2,71 | 3,84 | 5,41 | 6,64 | 10,83 |
| 2 | 4,60 | 5,99 | 7,82 | 9,21 | 13,82 |
| 3 | 6,25 | 7,81 | 9,84 | 11,34 | 16,27 |
| 4 | 7,78 | 9,49 | 11,67 | 13,28 | 18,46 |
| 5 | 9,24 | 11,07 | 13,39 | 15,09 | 20,52 |
| 6 | 10,64 | 12,59 | •с 15,03 | 16,81 | 22,46 |
| 7 | 12,02 | 14,07 | 16,62 | 18,48 | 24,32 |
| 8 | 1336 | 15,51 | 18,17 | 20,09, | - 26,12 |
| 9 | 14,68 | 16,92 | 19,68 | 21,67 | 27,88 |
| 10 | 15,99 | 18,31 | 21,16 | 23,21 | 29,59 |
| 11 | 17,28 | 19,68 | 22,62 | 24,72 | 31,26 |
| 12 | 18,55 | 21,03 | 24,05 | 26,22 | 32,91 |
| 13 | 19,81 | 22,36 | 25,47 | 27,69 | 34,53 |
| 14 | 21,06 | 23,68 | 26,87 | 29,14 | 36,12 |
| 15 | 22,31 | 25,00 | 28,26 | 30Л8 | 37,70 |
| 16 | 23,34 | 26,30 | 29,63 | 32,00 | 39,25 |
| 17 | 24,77 | 27,59 | 31,00 | 33,41 | 40,79 |
| 18 | 25,99 | 28,87 | 32,35 | 34,81 | 42,31 |
| 19 | 27,20 | 30,14 | 33,69 | 36,19 | 43,82 |
| 20 | 28,41 | 31,41 | 35,02 | 37,57 | 45,32 |
| 25 | 37,6 | 44,3 | |||
| 30 | 43,8 | 50,9 | |||
| 35 | 49,8 | 57,3 | |||
| 40 | 55,8 | 63,7 | |||
| 45 | 61,7 | 70,0 | |||
| 50 | 67,5 | 76,2 | |||
| 60 | 79,1 | 88,4 | |||
| 70 | 90.5 | 100 | |||
| 80 | 102 | 112 | |||
| 90 | 113 | 124 ' | |||
| 100 | 124 | 136 | |||
| 120 | 147 | 159 | |||
| 140 | 169 | 182 | |||
| 150 | 180 | 193 | |||
| 200 | 234 | 249 | |||
Окончание табл. 8.6
| Степень свободы V | Уровень значимости а | |||||
| 0,1 | 0,05 | 0,02 | 0,01 | 0,001 | ||
| 250 | 288 | 305 | ||||
| 300 | 341 | 360 | ||||
| 400 | 448 | 469 | ||||
| 500 | 553 | 576 | ||||
| 600 | 658 | 683 | ||||
| 700 | 763 | 790 | ||||
| 800 | 867 | 896 | ||||
| 900 | , 971 | 1002 | ||||
| 1000 | 1075 | 1107 | ||||
Величина q - 1 - а называется доверительной вероятностью (при уровне значимости 0,05 доверительная вероятность равна 0,95, при уровне значимости 0,01 0,99 и т. д.).
Под числом степеней свободы (v) понимают разность между числом измеряемых (наблюдаемых) значений и числом связей, возникающих между ними. Статистические таблицы содержат данные для различного числа степеней свободы.
Часто при обработке результатов психофизиологического обследования возникает задача сравнения показателей, не имеющих совместного распределения, например, тестовых показателей, полученных на разных (несвязанных) выборках. В этом случае проверяется предположение 0 принадлежности 1-й и 2-й выборок к одной генеральной совокупности, вычисляют г-критерий Стьюдента по формулам (8.29)-(8.31)
Число степеней свободы в этом случае рассчитывают так: "
V = n1+/i2-2. (8.31)
Рассчитанные значения г-критерия сравнивают с его критическим значением forv, пользуясь таблицей теоретического распределения Стьюдента (табл. 8.7).
Таблица 8.7
Граничные значения f-критерия Стьюдента
| для | уровня | значимо | сти 0,05 | , 0,01 и | 0,001 | ||
| V | 0,05 | 0,01 | 0,001 | V | 0,05 | 0,01 | 0,001 |
| 1 | 12,71 | 63,66 | — | 21 | 2,08 | 2,83 | 3.S2 |
| 2 | 4,30 | 9,92 | 31,60 | 224 ТТ | 2,07 | 2,82 | 3,79 |
| 3 | 3,18 | 5,84 | 12,92 | 23 Л | 2,07 | 2,81. | 3,77 |
| 4 | 2,78 | 4,60 | 8,61 | 24 | 2,06 | 2,80 | 3,75 |
| 5 | 2,57 | 4,03 | 6,87 | 25 | 2,06 | 2,79 | 3,73 |
| 6 | 2,45 | 3,71 | 5,96 | 26 | 2,06 | 2,78 | 3,71 |
| 7 | 2,37 | 340 | 5,41 | 27 | 2,05 | 2,77 | • * |
| 8 | 2,31 | 3,36 | 5,04 | 28 | 2,05 | 2,76 | 3,69 |
| 9 | 2,26 | 3,25 | 4,78 | 29 | 2,05 | 2,76 | 3,66 |
| 10 | 2,23 | 3,17 | 4,59 | 30 | 2,04 | . 2,75 | 3,65 |
| 11 | 2,20 | 3,11 | 4,44 | 40 | 2,02 | 2,70 | 345 |
| 12 | 2,18 | 3,05 | 4,32 | 50 | 2,01 | 2,68. | 3,50 |
| 13 | 2,16 | 3,01 | 4,22 | 60 | 2,00 | , 2,66 | 3,46 |
| 14 | 2,14 | 2,98 | 4,14 | ' 80 | 1,99 | 2,64 | 3,42 |
| 15 | 2,13 | 2,95 | 4,07 | 100 | 1,98 | 2,63 | 3,39 |
| 16 | 2,12 | 2,92 | 4,02 | 120 | 1,98 | 2,62 | 3,37 |
| 17 | 2,11 | 2,90 | 3,97 | 200 | 1,97 | 2,60 | 3,34 |
| 18 | 2,10 | 2,88 | 3,92 | 500 | 1,97 | 2,59 | 3,31 |
| 19 | 2,09 | 2,86 | 3,88 | 1,96 | 2,58 | 3,29 | |
| 20 | 2,09 | 2,85 | 3,85 |
Примечание. Нулевая, гипотеза о сходстве принимается при t <; tccv, а - 0,05 и отклоняется при t> tax, а = 0,01; v = v1 + v2= 2.
Вопросы для самоконтроля
1.Что такое статистическая взаимосвязь?
2. Какие основные методы оценки взаимосвязи двух признаков вы знаете?
3.Задание для самостоятельной подготовки
4.Используя данные (с. 524), рассчитайте парные линейные коэффициент корреляции Пирсона (г) и коэффициенты детерминации (D).
Для справки:
RegNum — регистрационный номер обследуемого;
Psd — показатель сердечной деятельности по пробе Руфье;
Stest, КОТ— тесты оценки уровня интеллектуального развития;
NPU — уровень нервно-психической устойчивости;
N — направленность на выполнение деятельности (мотивация);
D — экспертная оценка успешности профессиональной деятельности по 10-балльной шкале.
Оцените силу взаимосвязи между показателями тестов и экспертной оценкой успешности профессиональной деятельности.
Вопросы для тестового контроля знаний
1. Строгое соответствие каждого значения одного показателя определенному значению другого показателя называется:
а) функциональная взаимосвязь;
б) статистическая взаимосвязь;
в) все ответы верны;
г) все ответы неверны.
2. Соответствие каждого значения одного показателя нескольким более или менее близким значениям другого показателя называется:
а) функциональная взаимосвязь;
б) статистическая взаимосвязь;
в) все ответы верны;
г) все ответы неверны.
3.Взаимосвязь двух психодиагностических показателей, измеренных в шкале отношений или интервалов при линейной форме взаимосвязи, рассчитывается с помощью:
а) коэффициента Пирсона;
б) коэффициента Спирмэна;
в) коэффициента сопряженности;
г) коэффициента детерминации;
д) все ответы верны;
е) все ответы неверны.
4. Взаимосвязь показателей, измеренных в ординальной шкале, оценивается с помощью:
а) коэффициента Пирсона;
б) коэффициента Спирмэна;
в) коэффициента сопряженности;
г) коэффициента детерминации;
д) все ответы верны;
е) все ответы неверны.
5. Взаимосвязь показателей, измеряемых в шкале наименований, оценивается с помощью:
а) коэффициента Пирсона;
б) коэффициента Спирмэна;
в) коэффициента сопряженности;
г) коэффициента детерминации;
д) все ответы верны;
е) все ответы неверны.
6. Доля вариации одного показателя, которую можно объяснить за счет вариации другого показателя, называется:
а) коэффициентом Пирсона;
б) коэффициентом Спирмэна;
в) коэффициентом сопряженности;
г) коэффициентом детерминации;
д) все ответы верны;
е) все ответы неверны.
