1. Психометрические основы анализа результатов психологического и психофизиологического обследования
Психодиагностические тесты позволяют дать более или менее точную количественную характеристику изучаемых свойств. Тесты являются средством измерения, т. е. инструментом обоснованного и строгого отображения степени выраженности изучаемого свойства на числовую ось. Роль тестового измерения состоит в том, что в результате его применения появляется возможность использования математических методов. Если оперирование самими объектами исследования или их качественными признаками представляет определенную трудность в психодиагностике, то оперирование числовыми значениями, как правило, затруднений не вызывает. После выполнения математической обработки и статистического анализа полученные числовые данные могут быть вновь спроецированы на свойства изучаемых объектов, что позволяет осуществить содержательную интерпретацию тестовых результатов на более высоком уровне обобщения, чем это было возможно до измерения.
Таким образом, основная цель измерения в психодиагностике — получение численных эквивалентов степени выраженностиисследуемого свойства. Измерения в психодиагностике различаются по типу используемых шкал (уровню измерений).
Шкала наименований (номинальная шкала) представляет собой совокупность значений, соответствующих определенным качественным состояниям исследуемого объекта. Эта шкала служит для обнаружения и различения изучаемых объектов (например, по признаку пола: мужской — 1; женский — 2). Шкала наименований позволяет установить тождество объектов по оцениваемому признаку, но не отображает отношений типа «больше — меньше», поэтому большинство математических операций неприменимы для тестовых признаков, выраженных в этой шкале. Значения номинальной шкалы используются для подсчета частоты встречаемости того или иного признака в данной совокупности наблюдений.
Шкала порядка (ординальная шкала) представляет собой последовательность чисел, отражающих порядковое место (ранг) исследуемых объектов по степени выраженности оцениваемого свойства. Ординальная шкала позволяет не только установить факт равенства или неравенства измеряемых объектов, но и определить характер неравенства типа: «больше — меньше», «лучше — хуже» и т. п. Ограниченность ординальной шкалы заключается в том, что она отражает величину интервалов степени выраженности оцениваемого свойства у объектов, имеющих различные ранги. Ранговые места в выборках различной численности не имеют прямого соответствия и должны подвергаться пересчету, чтобы определить «взвешенные» ранговые места.
Шкала интервалов — это такая шкала, в которой оценка выраженности исследуемого свойства определяется по величине (интервалу) ее отклонения от условного значения, принятого за нулевую точку. Сравнение значений исследуемого свойства, измеренного в шкале интервалов, может осуществляться с точки зрения «насколько больше», но не «во сколько раз больше». Например, если температура повысилась с 10 до 20 °С, то это не означает, что стало в два раза теплее.
Шкала отношений — такая шкала, в которой оценка выраженности исследуемого свойства определяется отклонением от строго определенной нулевой точки, означающей отсутствие признака. В отличие от шкалы интервалов, значения оцениваемого свойства (например, рост, масса, скорость и т. п.) могут рассматриваться с точки зрения «во сколько раз одно из них больше или меньше другого». Обобщенные сведения об уровнях измерения представлены в табл. 8.1.
Таблица 8.1
Характеристика уровней измерения
| Уровни измерения | Основные операции | Допустимые математические процедуры | Примеры |
| Номинальный | Установление равенства | Число случаев Мода Корреляция случайных событий (тетра- и полихорические коэффициенты корреляции) | Нумерация испытуемых Пол испытуемых |
| Ординальный | Установление соотношений «больше» или «меньше» | Медиана Ранговая корреляция Ранговые критерии Проверка гипотез | Результаты ранжирования испытуемых экспертами |
| Интерваль ный | Установление равенства интервалов | Среднее, Среднее квадратическое (стандартное) отклонение | Календарные даты (время) Температура по Цельсию |
| Отношений | Установление равенства отношений | Коэффициент вариации Среднее геометрическое | Длина, сила, масса, скорость |
В психодиагностике измерения производятся чаще всего на одном из первых трех уровней, имеющих уже указанные ограничения вычисления статистических параметров и допустимости арифметических операций.
С точки зрения общей теории измерений, каждый тестовый результат представляет собой количественно измеренную величину оцениваемого свойства. Оцениваемое качество, для которого свойственно варьирование (рассеяние, разброс) степени выраженности, называется переменной, или случайной величиной. Случайная величина как статистическая категория характеризуется тем, что, хотя ее конкретное значение при единичном измерении заранее неизвестно, вероятность регистрации конкретного значения этой случайной величины подчиняется определенной закономерности — закону распределения.
Случайные величины подразделяются на два типа: непрерывные и дискретные. Непрерывные величины могут принимать любые значения (как целые, так и дробные) в определенном интервале, характерном для каждой такой случайной величины. Дискретные случайные величины могут принимать только конечное (ограниченное) количество точных значений, чаще всего выражаемых целыми числами (1, 2 и т. д.).
Конкретное единичное значение случайной величины называется вариантой. Группа вариант, полученных в аналогичных условиях измерения, образует совокупность вариант. Если в эту группу входят все без исключения варианты, характеризующие исследуемую общность (например, данные обследования всех сотрудников учреждения), то такая совокупность называется генеральной. Если условия не позволяют получить все возможные варианты (при исследованиях больших общностей), то рассматривается часть вариант, входящих в генеральную совокупность, выборка. Возможность переноса закономерностей, выявленных в частной выборке, на всю генеральную совокупность зависит от репрезентативности (представительности) выборки. Репрезентативность связана с полнотой отражения основных особенностей генеральной совокупности теми вариантами, которые вошли в выборку. Репрезентативность тем выше, чем больше объем выборки — число наблюдений (п) приближается к объему (численности) генеральной совокупности. Если исследованием охваченався генеральная совокупность, оно называется сплошным. Все остальные исследования относятся к выборочным.
Для удобства представления информации результаты измерения подвергают определенным процедурам (ранжирование, группирование). Ранжированием называется расстановка вариант в порядке их возрастания или убывания. При описании и обработке выборок большого объема прибегают к группировке вариант по интервалам. В простейшем случае используется разделение на две полярные группы (например, «лучшие» и «худшие»). Рекомендуемое количество диапазонов измерения для выборок разного объема представлено в табл. 8.2.
Таблица 8.2
Рекомендуемое число интервалов дли выборок разного объема
| Объем выборки (п) | 10-20 | 30-50 | 60-90 | 100-200 | 300-400 |
| Число интервалов (к) | 4 | 5-6 | 7 | 8 | 9 |
Величина или шаг интервала (К) определяется по формулам (8.1) и (8.2)
 (8.1)
(8.1)

Частота, или встречаемость, значений выборки в каждом интервале определяется числом результатов измерения, попавших в соответствующий данному интервалу диапазон значений.
Накопленная частота — сумма частот предыдущих интервалов вариационного ряда. Сумма частот всех интервалов равна объему выборки.
Относительная частота, или частость, определяется отношением соответствующей частоты к объему выборки.
Накопленная частость — сумма частостей предыдущих интервалов вариационного ряда. Сумма частостей всех интервалов равна единице.
Анализ вариационных рядов упрощается при их графическом представлении в виде полигона или гистограммы распределения (рис. 8.1).

Рис. 8.1. Пример полигона распределения (а) и гистограммы (б): по оси абсцисс — величина показателя, по оси ординат — частоты
При анализе фактических результатов измерения — эмпирического распределения оценок— делают предположение о том распределении, которое имела бы выборка, если бы число наблюдений было очень большим (сравнимым с объемом генеральной совокупности). Распределение вариант генеральной совокупности называется теоретическим распределением. График теоретического распределения может быть получен из полигона эмпирического распределения при бесконечном увеличении числа наблюдений и сужении интервалов до размеров точки (отдельного значения выраженности исследуемого свойства). Большинство измерений, применяемых в психодиагностике, подчиняется закону нормального распределения. График нормального распределения представляет собой куполообразную! кривую, симметричную относительно центра группирования. Кривая имеет строго определенные пропорции и описывается формулой (8.3)

где х — среднее арифметическое;/— частота или плотность распределения; а — среднее квадратическое отклонение; я и е — константы, равные 3,141... и 2,718... соответственно; х — результаты измерений.
Среднее арифметическое значение и среднее квадратическое отклонение — основные параметры распределения случайных величин. Среднее арифметическое неупорядоченного ряда измерений вычисляют по формуле (8.4)
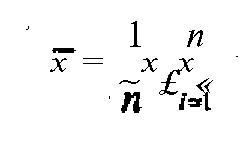

Символ £ обозначает сумму всех значений х(, когда i принимает значения от 1 до п (£ — знак суммирования, внизу и вверху которого указываются пределы суммирования — «от» и «до»; х — общий член последовательности, подлежащий суммированию; i — индекс суммирования, порядковый номер члена последовательности).
Среднее квадратическое отклонение (а) — мера рассеяния вариант. Для определения величины а проводится ряд последовательных вычислений:
1. Вычисляются отклонения (d) каждой конкретной варианты от среднего арифметического
 (8.5.)
(8.5.)
2. Вычисляются возведенные в квадрат значения отклонений
 (8.6)
(8.6)
3. Вычисляется сумма возведенных в квадрат отклонений - вариация
 (8.7)
(8.7)
4. Вычисляется «взвешенная» сумма квадратов отклонений дисперсия
 (8.8.)
(8.8.)
4.1. В выборках, где п < 30, используется формула
 (8-9)
(8-9)
5. Вычисляется значение квадратного корня из величины дисперсии, собственно — среднее квадратическое отклонение

При нормальном распределении наибольшее отклонение крайней варианты от средней арифметической составляет примерно 3d (правило «трех сигм»), а разность между наибольшей и наименьшей вариантами близка к 6а.
Закономерности варьирования результатов измерений, распределение которых соответствует нормальному, используются для конструирования различных оценочных шкал. Имеется определенное статистическое соответствие между отклонением варианты от среднего арифметического и ранговым положением ее в упорядоченном вариационном ряду. Кривая нормального распределения с процентным выражением распределений относительных и накопленных частостей в зависимости от величины отклонения от среднего арифметического значения, а также в связи с наиболее часто применяющимися стандартными оценочными шкалами представлена на рис. 8.2.

Простейшей из стандартных шкал является Z-шкала. Первичные значения показателя могут быть преобразованы в Z-оценки по формуле (8.11)
 (8.11)
(8.11)
где х— среднее арифметическое показателя; х< — величина показателя теста; а — среднее квадратическое отклонение.
Положительные значения Z-оценки соответствуют величинам выше среднего уровня, отрицательные значения— величинам ниже среднего. Единицей этой шкалы измерения является величина среднего квадратического отклонения. Среднее значение шкалы Z-оценок равно нулю. Использование Z-оценок не всегда удобно, так как они могут принимать отрицательные и дробные значения. Поэтому часто Z-оценки преобразуют в другие шкалы, имеющие заданные среднее квадратическое отклонение и среднее значение. При этом используется формула (8.12)
x*=o,xZ,+x„ (8.12)
где ха — заданное среднее значение шкалы; аа — заданное среднее квадратическое отклонение.
Наиболее типичные стандартные показатели, получаемые на основе Z-оценок:
1. Коэффициент интеллекта IQ

Широко используется шкала Т (среднее значение — 50 единиц, среднее квадратическое отклонение — 10 единиц). Широкий диапазон измерения, высокая дробность оценок ТЛшкалы позволяет проводить тонкую дифференциацию испытуемых по величине тестовых показателей. При решении практических вопросов профессионального отбора приемлемы и более «грубые» оценочные шкалы. Для большинства тестов достаточно использования 10-балльных шкал. Наиболее распространенной является шкала стенов, имеющая среднее значение 5,5 единицы и среднее квадратическое отклонение — 2 единицы.
В тех случаях, когда распределение первичных показателей тестов не описывается кривой нормального распределения или выборка небольшая, бывает удобно пользоваться преобразованиями первичных значений показателей, не опираясь на характер распределения. В этом случае оценочные шкалы строятся на основе параметров частотного распределения: перцентили, децили, квартили. При таком подходе все первичные значения показателя группируются по заранее выбранным интервалам. Подсчитанное таким способом число является частотой (количеством случаев) для соответствующего интервала. При этом сумма всех частот по всем интервалам равняется общему числу случаев в выборке. Информация о частотном распределении может быть представлена в виде таблиц или в виде кумулятивной кривой. Под перцентилем понимается процентная доля индивидов из выборки стандартизации, первичный результат которых ниже данного первичного показателя. Например, если 28% людей правильно решают 15 задач в тесте на арифметическое мышление, то первичному показателю 15 соответствует 28-й перцентиль. Перцентили указывают на относительное положение индивида в выборке стандартизации. Их можно рассматривать как ранговые градации, общее число которых равно 100, с той разницей, что при ранжировании принято начинать отсчет сверху, т. е. с лучшего члена группы. В случае перцентилей отсчет ведется снизу — это означает, что чем ниже перцентиль, тем хуже позиция индивида по этому качеству. 50-й перцентиль соответствует медиане. Перцентили свыше 50 представляют показатели выше среднего, а те, которые лежат ниже 50, — сравнительно низкие показатели. 25-й и 75-й перцентили известны также под названием 1-го и 3-го квартилей, поскольку они выделяют нижнюю и верхнюю четверти распределения. Как и медиана, они удобны для описания распределения показателей и сравнения с другими распределениями.
Перцентильные показатели обладают рядом достоинств. Их легко рассчитать и понять даже сравнительно неподготовленному в статистике человеку. Применение их достаточно универсально, они одинаково применимы к различным возрастным группам и подходят к любому типу теста, они измеряют способности или свойства личности.
Главный недостаток перцентилей связан с неравенством их как единиц измерения, особенно на краях распределения. Если распределение первичных показателей приближается к нормальной кривой, то различия между первичными показателями вблизи медианы в перцентильном выражении преувеличены, тогда как аналогичные различия вблизи краев распределения сильно занижены.
Зависимость между перцентилями и другими типичными стандартными показателями показаны в табл. 8.3.
Таблица 8.3
Зависимость между перцентилями, Z-оценками и Г-оценками
| Перцентиль | Z-оценка | Г-оценка |
| 1 | -2,33 | 27 - |
| 5 | -1,64 | 34 |
| 10 | -1,28 | 37 |
| 15 | -1,04 | 40 |
| 20 | -0,84 | "4 2 |
| 25 | -0,67 | 43 |
| 30 | -0,52 | 45 |
| 35 | -0,39 | 46 |
| • 40 | -0,25 | 48 |
| 45 | -0,13 | 49 |
| 50 | 0,00 | 50 |
| 55 | 0,13 | 51 |
Окончание табл. 8.3
| Перцентиль | Z-оценка | Г-оценка |
| 60 | 0,25 | 52 |
| 65 | 0,39 | 54 |
| 70 | 0,52 | 55 |
| 75 | 0,67 | 57 |
| 80 | 0,84 | 58 |
| 85 | 1,04 | 60 |
| 90 | 1,28 | 63 |
| 95 | 1,64 | 66 |
| 99 | 2,33 | 73 |
Резюмируя сказанное, можно заключить, что перцентили показывают относительное положение каждого индивида в нормативной выборке, а не величину различия между результатами тестирования.
Известны и другие, более сложные виды прербразований первичных показателей в нормативно-оценочные шкалы, дающие лучшие со статистической точки зрения результаты. К ним можно отнести преобразования, выполненные на основе функций принадлежности, полиномов.
Вопросы для самоконтроля
5. Что такое измерение в психодиагностике?
6. Что вкладывается в понятия «переменные величины», «показатели», «признаки»?
7. Какие шкалы измерений используются в психодиагностике и каковы их основные особенности?
8. Что такое стандартизация шкал измерений и каковы наиболее типичные стандартные показатели?
9. В чем смысл предварительного анализа данных?
10. Какими основными описательными статистиками характеризуются переменные величины?
11. Что такое статистическая группировка?
12. ЧТО такое нормальное распределение и каковы его основные свойства?
Вопросы для тестового контроля знаний
1. Допустимыми математическими процедурами при измерении Данных психодиагностического обследования в шкале наименований являются:
а) число случаев, мода, корреляция случайных событий (тет- ра- и полихорические коэффициенты корреляции);
б) медиана, ранговая корреляция, ранговые критерии, проверка гипотез;
в) среднее, среднее квадратическое (стандартное) отклонение;
г) коэффициент вариации, среднее геометрическое;
д) все ответы верны;
е) все ответы неверны.
2. Допустимыми математическими процедурами при измерении данных психодиагностического обследования в ординальной шкале являются: -
а) число случаев, мода, корреляция случайных событий (тет- ра- и полихорические коэффициенты корреляции);
б) медиана, ранговая корреляция, ранговые критерии, проверка гипотез;
в) среднее, среднее квадратическое (стандартное) отклонение;
г) коэффициент вариации, среднее геометрическое;
д) все ответы верны;
е) все ответы неверны.
3. Допустимыми математическими процедурами при измерении данных психодиагностического обследования в интервальной шкале являются:
а) число случаев, мода, корреляция случайных событий (тет- ра- и полихорические коэффициенты корреляции);
б) медиана, ранговая корреляция, ранговые критерии, проверка гипотез;
в)среднее, среднее квадратическое (стандартное) отклонение;
г) коэффициент вариации, среднее геометрическое;
д) все ответы верны;
е) все ответы неверны.
4. Допустимыми математическими процедурами при измерении данных психодиагностического обследования в шкале отношений являются:
а) число случаев, мода, корреляция случайных событий (тет- ра- и полихорические коэффициенты корреляции);
б) медиана, ранговая корреляция, ранговые критерии, проверка гипотез;
в) среднее, среднее квадратическое (стандартное) отклонение;
г) коэффициент вариации, среднее геометрическое;
д) все ответы верны;
е) все ответы неверны.
5. Совокупность вариант, в состав которой входят все без исключения варианты, характеризующие исследуемую общность, называется:
а) генеральной совокупностью;
б) выборочной совокупностью;
в) сплошным исследованием.
6. Среднее квадратическое отклонение — это:
а) мера отклонения среднего арифметического значения выборочной совокупности от математического ожидания (среднего значения генеральной совокупности;
б) мера рассеяния вариант выборочной совокупности;
в) отклонение куполообразной кривой нормального распределения от центра.
7. Шкала стенов представляет собой:
а) 7-балльную шкалу;
б) 9-балльную шкалу;
в) 10-балльную шкалу;
г) 50-балльную шкалу;
д) 100-балльную шкалу.






