Рассмотрим использование обобщенного метода наименьших квадратов для корректировки гетероскедастичности возмущений. Пусть строится линейная регрессионная модель (1). Будем считать, что модель гетероскедастична, т. е. дисперсии возмущений 
(i =1, 2, …, n) не равны между собой, а сами возмущения не коррелированны и их математические ожидания равны нулю. Это означает, что ковариационная матрица вектора возмущений W будет диагональной:
 .
| (25) |
Для оценки параметров такой модели используется взвешенный метод наименьших квадратов (Weighted Least Squares), являющийся частным случаем обобщенного МНК.
Сущность взвешенного метода наименьших квадратов состоит в том, что каждый квадрат остатка 
(i =1, 2, …, n) «взвешивается» с помощью коэффициента 
, где s(e i) — среднее квадратическое отклонение i -го возмущения. Тем самым добиваются равномерного вклада остатков в остаточную сумму квадратов, что приводит, в конечном счете к получению несмещенных и наиболее эффективных оценок параметров модели.
Условие взвешенного метода наименьших квадратов имеет вид:
 .
| (26) |
Вектор b* оценок параметров модели определяется по формуле (24).
На практике, однако, средние квадратические отклонения возмущений s(e i) почти никогда не бывают известны. Поэтому для применения взвешенного метода наименьших квадратов, необходимо сделать предположение о значениях s(e i). Весьма часто считают, что среднее квадратическое отклонение возмущений пропорционально значениям одного из факторов, предположительно делающих выборочную совокупность неоднородной.
Пусть имеются исходные данные для построения модели множественной регрессии (табл. 1).
| Таблица | 1 |
| Исходные данные для построения модели множественной регрессии |
| Номер наблюдения (объекта) | Значение результата Y | Набор факторов и их значения | ||||||
| X 0 | X 1 | X 2 | … | Xj | … | Xp | ||
| y 1 | x 11 | x 12 | … | x 1 j | … | x 1 p | ||
| y 2 | x 21 | x 22 | … | x 2 j | … | x 2 p | ||
| … | … | … | … | … | … | … | … | … |
| i | yi | xi 1 | xi 2 | … | xij | … | xip | |
| … | … | … | … | … | … | … | … | |
| n | yn | xn 1 | xn 2 | … | xnj | … | xnp |
Представим модель (1) в развернутом виде:
 (i =1, 2, …, n).
| (27) |
Если предположить, что среднее квадратическое отклонение возмущений s(e i) (i =1, 2, …, n) пропорционально значениям xij фактора Xj (или, что одно и тоже — дисперсия возмущений 
пропорциональна квадрату значений фактора Xj), то исходные данные преобразуются их делением на соответствующие значения xij (i =1, 2, …, n). Такое преобразование называется масштабированием исходных данных по фактору Xj. (табл. 2).
| Таблица | |
| Масштабирование исходных данныхпо фактору Xj |
| Номер наблюдения (объекта) | Значение результата Y | Набор факторов и их значения | ||||||
| X 0 | X 1 | X 2 | … | Xj | … | Xp | ||
| y 1/ x 1 j | 1/ x 1 j | x 11/ x 1 j | x 12/ x 1 j | … | … | x 1 p / x 1 j | ||
| y 2/ x 2 j | 1/ x 2 j | x 21/ x 2 j | x 22/ x 2 j | … | … | x 2 p / x 2 j | ||
| … | … | … | … | … | … | … | … | … |
| i | yi / xij | 1/ xij | xi 1/ xij | xi 2/ xij | … | … | xip / xij | |
| … | … | … | … | … | … | … | … | … |
| n | yn / xnj | 1/ xnj | xn 1/ xnj | xn 2/ xnj | … | … | xnp / xnj |
Таким же образом преобразуется и модель (27):
 (i =1, 2, …, n),
| (28) |
или, что одно и тоже —
 (i =1, 2, …, n),
| (29) |
Введем обозначения.
Пусть 
, 
, 
, 
, …, 
, 
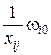, тогда преобразованная модель окончательно будет иметь вид:
 (i =1, 2, …, n).
| (30) |
Параметры преобразованной модели (30) оцениваются обычным методом наименьших квадратов. Если предположение о пропорциональности среднего квадратического отклонения возмущений значениям фактора Xj имеет основание, то «новое» возмущение n i будет иметь постоянную и притом — наименьшую дисперсию, а коэффициенты уравнения регрессии окажутся несмещенными и эффективными оценками параметров модели (30). Вместе с тем следует иметь в виду, что новые преобразованные переменные получают другое экономическое содержание и их регрессия имеет иной смысл, чем регрессия по исходным данным. Поэтому численно оценки параметров моделей (27) и (30) в общем случае не совпадают.
Если строится линейная модель парной регрессии Y по X
 (i =1, 2, …, n),
| (31) |
то она трансформируется в модель
 (i =1, 2, …, n),
| (32) |
в которой свободный член и угловой коэффициент как бы поменялись местами.
На практике иногда имеет смысл попробовать использовать одновременно несколько факторов для масштабирования исходных данных. Если каждый раз получаются сходные результаты и тесты Голдфельда–Квандта по всем факторам не выявляют гетероскедастичность возмущений, то эту проблему можно считать решенной.
В ряде случаев дисперсия возмущений зависит не от включенных в модель факторов, а от тех, которые не включены в модель, но играют существенную роль в исследуемой зависимости. Иногда для устранения гетероскедастичности необходимо изменить спецификацию модели, например, линейную на логарифмическую и т.д.
Пример 1
По 12 транспортным компаниям исследуется зависимость годового дохода (переменная Y, млн. руб.) от среднегодового количества грузовых автомобилей (переменная X). Имеются данные, для удобства упорядоченные по фактору X:
| № п/п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| X | 15 | 18 | 22 | 27 | 25 | 31 | 34 | 37 | 40 | 45 | 48 | 48 |
| Y | 235 | 250 | 247 | 287 | 260 | 262 | 307 | 280 | 357 | 410 | 389 | 311 |
Требуется:
1. Построить линейную модель парной регрессии Y по X.
2. Проверить наличие гетероскедастичности возмущений методом Голдфельда–Квандта.
3. При обнаружении гетероскедастичности возмущений построить взвешенную модель регрессии.
Решение
1. По исходным данным строим линейную модель парной регрессии
(i =1, 2, …, n; n=12).
Параметры модели оцениваем обычным методом наименьших квадратов. С помощь табличного процессора MS Excel были определены коэффициенты уравнения регрессии 
: b0=160,6; b1=4,277. Таким образом, уравнение примет вид:
.
Уравнение регрессии статистически значимо на уровне a=0,05: F‑статистика имеет значение F=25,15; табличное значение F-критерия Фишера — F0,05; 1;10=4,96; коэффициент детерминации — R2=0,716.
Значение углового коэффициента уравнения регрессии b1=4,277 показывает, что увеличение количества автомобилей на одну единицу приводит к росту годового дохода в среднем на 4,277 млн. руб.
Визуальный анализ графика зависимости годового дохода от количества автомобилей дает основание предполагать наличие гетероскедастичности возмущений. Видно, что отклонение от линии регрессии наблюдений, соответствующих крупным предприятиям, больше, чем для малых предприятий:
2. Построим график остатков и проведем его визуальный анализ. Предсказываемые уравнением регрессии значения результата 
и остатков (i =1, 2, …, n; n=12) приведены в таблице:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| xi | 15 | 18 | 22 | 27 | 25 | 31 | 34 | 37 | 40 | 45 | 48 | 48 |
| yi | 235 | 250 | 247 | 287 | 260 | 262 | 307 | 280 | 357 | 410 | 389 | 311 |
| 225 | 238 | 255 | 276 | 268 | 293 | 306 | 319 | 332 | 353 | 366 | 366 |
| ei | 10 | 12 | -8 | 11 | -8 | -31 | 1 | -39 | 25 | 57 | 23 | -55 |
График остатков по фактору X показан на рисунке:
Визуальный анализ графика остатков показывает, что их разброс растет по мере увеличения фактора Х, что может свидетельствовать о гетероскедастичности возмущений. Проверим это предположение методом Голдфельда–Квандта. Будет считать, что возмущения распределены по нормальному закону и их среднее квадратическое отклонение пропорционально значению фактора Х. Все остатки уже упорядочены по Х. Выбираем 
первых и последних остатков. По каждой из групп определяем сумму квадратов остатков:
;
.
Так как SS2>SS1, то F-статистику рассчитываем по формуле
.
Табличное значение F-критерия Фишера для уровня значимости a=0,05 и чисел степеней свободы числителя и знаменателя 
(где p=1 — число факторов в модели) составляет F0,05; 3;3=9,28.
Так как 
, статистическая гипотеза об одинаковой дисперсии возмущений отклоняется на уровне значимости a=0,05. Факт наличия гетероскедастичности возмущений считается установленным.
3. Применим взвешенный МНК к исходной модели в предположении, что среднее квадратическое отклонение возмущений пропорционально значению фактора Х, для чего масштабируем исходные данные по Х:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1/xi | 0,0667 | 0,0556 | 0,0455 | 0,0370 | 0,0400 | 0,0323 | 0,0294 | 0,0270 | 0,0250 | 0,0222 | 0,0208 | 0,0208 |
| yi/xi | 15,67 | 13,89 | 11,23 | 10,63 | 10,40 | 8,45 | 9,03 | 7,57 | 8,93 | 9,11 | 8,10 | 6,48 |
Исходную модель преобразуем в модель (i =1, 2, …, n; n=12). Оцениваем параметры преобразованной модели b1 и b0 обычным методом наименьших квадратов. С помощь MS Excel были определены коэффициенты уравнения регрессии 
преобразованной модели: b1=3,863; b0=173,2, и уравнение регрессии примет вид:
(F=106; R2= 0,914).
Угловой коэффициент данного уравнения сравнивают со свободным членом исходного уравнения регрессии и наоборот. Видно, что значения соответствующих параметров уравнений отличаются друг от друга.
Тест Голдфельда–Квандта, примененный к преобразованной модели, не выявляет гетероскедастичности ее возмущений: F-статистика 
не превышает табличное значение F-критерия Фишера 
.
Используя преобразованное уравнение регрессии делаем вывод, что увеличение количества автомобилей на одну штуку приводит к росту годового дохода в среднем на 3,863 млн. руб.
