Применение обобщенного метода наименьших квадратов для оценивания параметров эконометрических моделей
ПЛАН
1. ОБЫЧНЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ. 2
1.1. Предпосылки обычного метода наименьших квадратов. 2
1.2. Свойства оценок обычного метода наименьших квадратов. 5
2. ОБОБЩЕННЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ. 6
2.3. Обобщенная модель регрессии. 6
2.4. Оценивание параметров моделей с гетероскедастичностью возмущений. 10
Пример 1. 13
2.5. Оценивание параметров моделей с коррелированными возмущениями. 16
Пример 2. 16
ЛИТЕРАТУРА. 19
ОБЫЧНЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Предпосылки обычного метода наименьших квадратов
Пусть рассматривается возможность построения линейной модели множественной регрессии. В матричной форме модель имеет вид:
 ,
| (1) |
где Y — вектор значений результата Y размера n; X — матрица значений факторов размера 
; b — вектор параметров модели размера 
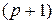; e — вектор возмущений размера n.
Уравнение регрессии модели (1) в матричной форме выглядит следующим образом:
 ,
| (2) |
где 
— вектор предсказываемых уравнением регрессии значений результата Y размера n; b — вектор оценок параметров модели по выборочным наблюдениям размера .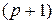
Указанные матрицы имеют вид:
; 
; 
; 
; 
; 
.
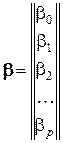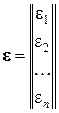Разность матриц Y и является вектором-столбцом остатков размера n:
 .
| (3) |
Условие обычного метода наименьших квадратов (Ordinary Least Squares) в матричной форме записывается как
 ,
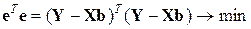| (4) |
откуда вектор оценок b параметров модели (1) определяется по формуле
 .
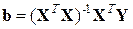| (5) |
(Индекс «T» обозначает операцию транспонирования матриц, а индекс «–1» — операцию обращения матриц.)
Для получения несмещенных, эффективных и состоятельных оценок параметров модели (1) необходимо выполнение следующих предпосылок:
1. Возмущение e i (i =1, 2, …, n) есть величина случайная, а факторы X 1, X 2, …, Xp — величины неслучайные. Это означает, что вектор возмущений e — случайный вектор, а матрица значений факторов X — неслучайная (детерминированная).
Проверка выполнения этой предпосылки может проводиться с помощью разных критериев. Наиболее простыми из них являются метод серий и метод поворотных точек, которыми исследуется ряд остатков регрессии. Иногда достаточным оказывается визуальный анализ графика (графиков) остатков.
2. Математическое ожидание возмущения равно нулю e i:
 (i =1, 2, …, n).
| (6) |
Другими словами, математическое ожидание вектора возмущений e есть нулевой вектор размера n:
 .
| (7) |
Данная предпосылка всегда выполняется для линейных моделей и моделей, нелинейных по переменным. Для моделей, нелинейных по параметрам и приводимых к линейному виду логарифмированием, предпосылка выполняется для логарифмов исходных данных.
3. Дисперсия возмущения одинакова для всех наблюдений результата Y:
 (i =1, 2, …, n).
| (8) |
Это условие называется условием гомоскедастичности или равноизменчивости возмущений. В матричной форме данная предпосылка имеет вид:
 ,
| (9) |
где I n — единичная матрица n -го порядка.
Выполнение этой предпосылки может проверяться разными методами. Ниже рассмотрена процедура проверки предпосылки методом Голдфельда–Квандта.
4. Возмущения не коррелированны между собой. Это означает, что ковариация между отдельными возмущениями e j и e k (
) равна нулю:
| (10) |
где m(e j) и m(e k) равны нулю в силу предпосылки 2.
Матричная форма записи предпосылки 4 имеет вид:
 ,
| (11) |
где 
— ковариационная матрица возмущений
 ,
| (12) |
в которой все элементы, не лежащие на главной диагонали, равны нулю, а все элементы, лежащие на главной диагонали, равны одной и той же дисперсии 
:
 (i =1, 2, …, n).
| (13) |
Равенство (13) вытекает из определения дисперсии и предпосылки 2. Так в соответствии с определением, дисперсией s2(Z) некоторой случайной величины Z называется математическое ожидание квадрата ее отклонения от математического ожидания: 
. Согласно предпосылке 2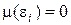 
, отсюда
 .
| (14) |
Видно, что матричные записи условий предпосылок 3 и 4 — (9) и (11) соответственно, совпадают. Проверка выполнения предпосылки 4 с помощью d ‑статистики Дарбина–Уотсона рассмотрена ниже.
5. Возмущение e i есть нормально распределенная случайная величина, а вектор возмущений e — нормально распределенный случайный вектор:
 .
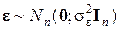| (15) |
Обоснованием такого допущения служит центральная предельная теорема теории вероятностей, согласно которой сумма большого числа случайных величин имеет приближенно нормальное распределение независимо от индивидуального распределения слагаемых. Отклонение фактических значений результата Y от теоретических вызывается, как правило, множеством случайных и неучтенных факторов, каждый из которых не оказывает доминирующего влияния. Поэтому нормальное распределение является приемлемой моделью суммарной погрешности, т. е. возмущения.
Выполнение этой предпосылки может проверяться разными способами, например, с помощью R / S -критерия.
6. Матрица 
является неособенной, т. е. ее определитель не равен нулю. Это означает, что столбцы матрицы значений факторов X должны быть линейно независимыми. Следовательно матрица X должна иметь максимальный ранг: 
, где p — число факторов в модели. Кроме того, число наблюдений n должно превосходить ранг матрицы X:
 ,
| (16) |
поскольку в противном случае невозможно получение сколько-нибудь надежных статистических выводов.
